Représentations graphiques de données statistiques - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Les résultats d'une enquête statistique peuvent donner lieu à de nombreuses représentations graphiques.
Représentation des effectifs et des fréquences.
Une règle générale distingue les représentations sans épaisseur (diagramme en bâtons) et les représentations avec épaisseur.
- Dans une représentation sans épaisseur, l'effectif (ou la fréquence) est proportionnel à la hauteur.
- Dès qu'une surface existe, l'effectif (ou la fréquence) est proportionnel à l'aire.
Cas des variables discrètes
Pour des variables quantitatives discrètes,
On privilégie le diagramme en bâtons.
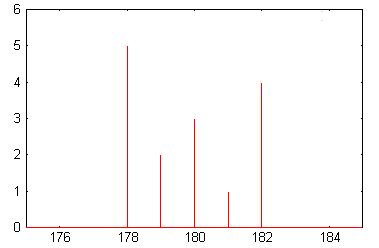
Diagramme en bâtons issu de l'article Statistiques élémentaires discrètes
Mais on voit apparaître parfois des représentations avec épaisseur.
- Le diagramme figuratif. Les effectifs sont représentés par des images (silhouettes, bâtiments, ...) rappelant la population étudiée. Ces images ont une taille proportionnelle à l'effectif. Il existe alors un danger de mauvaise représentation ou de mauvaise interprétation. Si un doublement de l'effectif correspond seulement à une allongement d'un facteur deux de l'image dans une seule direction, la règle des aires est respectée. Mais si le doublement de l'effectif correspond à une doublement de la taille de l'image, l'œil humain perçoit en réalité une multiplication par 4 (facteur 2 en largeur et facteur 2 en hauteur). L'interprétation de la représentation graphique est alors faussée.
- Le diagramme en rectangles. Si les rectangles ont même base, les hauteurs proportionnelles aux effectifs respectent la règle des aires.
- L'ajout d'un polygone rejoignant les sommets du diagramme en bâtons. Cette tentative de lissage de la représentation graphique ne respecte pas tout à fait la règle des aires (l'aire sous le polygone ne correspond pas tout à fait à l'effectif ou la fréquence) mais a le mérite de présenter une courbe se rapprochant de la courbe de densité de probabilité.
Pour des variables qualitatives,
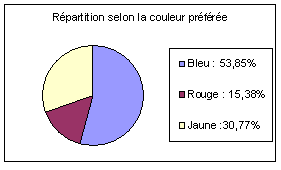
On utilise fréquemment les diagrammes circulaires dits en camembert (voir l'article Statistiques élémentaires discrètes) , demi-circulaire ou rectangulaire. On trouve aussi des diagrammes figuratifs avec le danger évoqué plus haut.
Cas des variables continues
- Voir article détaillé : histogramme
On utilise l'histogramme en respectant la règle des aires. Pour éviter tout danger, il est préférable de travailler avec des classes d'amplitude constante. Dans ce cas, les hauteur des rectangles sont proportionnelles aux effectifs (ou aux fréquences). Le cas des classes d'amplitudes variables se révèle plus délicat et est traité dans statistiques élémentaires continues. On trouve aussi pour les variables continues la même tentative de lissage avec la même réserve sur la règle des aires.
Représentation des effectifs cumulés.
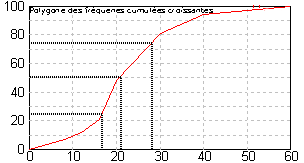
Pour les variables continues, on peut tracer le polygone des effectifs (ou fréquences) cumulés. Le principe du tracé est expliqué dans l'article statistiques élémentaires continues. Ce polygone, permet de lire très rapidement l'effectif d'un intervalle de la forme [x1,x] et , par différence, l'effectif de tout intervalle. Elle permet aussi de lire très rapidement les quartiles et les déciles. Cette représentation préfigure le tracé de la fonction de répartition en probabilité.
On voit apparaître parfois un polygone des effectifs cumulés pour des variables discrètes. En toute rigueur, il faudrait tracer un diagramme en escalier.
Nuage de points

On rencontre principalement cette représentation dans les séries statistiques à deux variables.
Elle apparaît aussi de manière moins identifiable dans les cartes géographiques ou météorologique (impact de la foudre, densité de population, présence d'industries,...). L'effectif est alors associé à une taille de point ou une couleur de fond.
Diagramme en boîte à moustaches
Ce diagramme résume seulement quelques caractéristiques de position du caractère étudié (médiane, quartiles, min/max ou déciles). Il est utilisé principalement pour comparer un même caractère dans deux populations de tailles différentes. Il s'agit de tracer un rectangle allant du premier quartile au troisième quartile et coupé par la médiane. On ajoute parfois des segments aux extrémités menant jusqu'aux valeurs min/max ou jusqu'au premier et neuvième décile. On parle alors de diagramme en boîte à moustaches ou à pattes.
Comparaison de diagramme en boîte à moustaches D1 / D9 avec
Q1 = 3, M = 7, Q3=12, D1 = 1, D9 = 16
Q1 = 7, M = 9, Q3=12, D1 = 1, D9 = 16
Sparklines
Les sparklines sont un format développé par Edward Tufte pour des mini-graphiques qui peuvent être insérés dans un texte sur une page.
Tufte décrit les sparklines comme des "graphiques intenses en données, de design simple, et ayant la taille d’un mot". Alors que le graphique typique est conçu de manière à montrer le plus de données possible et est exclut du flux de texte ; les sparklines sont concis, mémorables, et localisés précisément à l’endroit approprié.
| Sparklines U.S. stock market activity (February 7, 2006) |
|||
|---|---|---|---|
| Day | Index | Value | Change |
|
|
Dow Jones | 10765.45 | −32.82 (−0.30%) |
|
|
S&P 500 | 1256.92 | −8.10 (−0.64%) |
| Nasdaq | 2244.83 | −13.97 (−0.62%) | |
- Explication des sparklines par Edward Tufte
- BonaVista MicroCharts, Sparklines, bullet graphs et autres graphiques de cellule pour Excel. Les formules de graphiques dynamiques actualisent vos graphiques et sparklines multicolores.



















































