Arithmétique des polynômes - Définition

On suppose de L est une extension finie de R contenant strictement R, on va montrer que L est isomorphe à C. Dans un premier temps, montrons que :

• Le corps L contient une copie de C :

Soit α un élément de L qui ne soit pas dans R, comme L est un espace de dimension finie sur R, la famille (1, α,  α², ...,  αⁿ) est nécessairement liée par une combinaison linéaire à coefficients dans R et non triviale, si n est suffisamment grand. Notons cette combinaison linéaire nulle et non triviale :

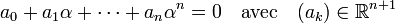
On choisit n le plus petit possible, c'est-à-dire que la famille (1, α,  α², ...,  α^n-1) est libre. L'entier n est au moins égal à 2 car sinon α serait un élément de R (sinon aurait la relation a₀ + a₁.α = 0, qui montrerait que α est réel). Si l'on substitue à α l'indéterminée X, on obtient un polynôme P, ayant pour racine dans L la valeur α. Ce polynôme est irréductible, car s'il ne l'était pas P s'écrirait Q.R et α serait racine soit de Q soit de R, ce qui donnerait une combinaison linéaire non triviale de degré strictement inférieur à n, ce qui est impossible par hypothèse.

Les seuls polynômes irréductibles de R de degré strictement supérieurs à 1, sont les polynômes de degré 2 et de discriminant négatif (cf l'article Factorisation des polynômes), ce qui montre que P est un polynôme de degré 2 et de discriminant négatif. On note δ la racine de l'opposé du discriminant. Si l'on considère maintenant le polynôme P comme un polynôme à coefficients dans L (ce qui est possible car L contient R, il n'est pas irréductible, car comme α est racine, le polynôme X - α divise P. Une considération de degré montre que la décomposition en facteurs irréductibles de P, considéré comme un polynôme de L[X] s'écrit :

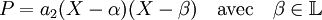
On a la relation classique, pour les racines des équations du second degré :

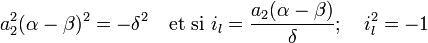
Le R espace vectoriel engendré par la base (1, i_l) est une copie de C contenue dans L, ce qui montre le résultat recherché.

• Le corps L est un copie de C :

On identifie maintenant l'espace vectoriel réel engendré par (1, i_l) à C, l'objectif est de montrer que L ne contient pas d'autres éléments que ceux inclus dans C. On peut maintenant considérer L comme un C espace vectoriel car c'est un corps contenant C. Il de dimension finie, comme R espace vectoriel, et donc il est aussi un espace vectoriel de dimension finie, comme C espace vectoriel. Soit γ un élément de L et (1, γ,  γ², ...,  γ^m) une famille liée dans le C espace vectoriel L, on choisit encore m minimal. Le polynôme Q construit comme précédemment est irréductible sur C. Le théorème fondamental de l'arithmétique montre que Q est nécessairement de degré 1 car tout polynôme irréductible à coefficients dans C est de degré 1 (cf l'article Factorisation des polynômes). Ceci montre que γ est un élément de C, car racine d'une équation de degré 1 à coefficients dans C. Autrement dit, tout élément de L est un élément de C, ce qui termine la démonstration.

Pour le démontrer, on raisonne par récurrence sur le degré n du polynôme. Si n est égal à 1, l'extension L est égale à K, supposons le résultat démontré pour tous les polynômes à coefficients dans une extension finie de K et de degré inférieur ou égal à n. Montrons que le résultat est vrai pour les polynômes de degré n + 1. Si la décomposition en facteur premiers du polynôme contient un polynôme Q₁, de degré 1, il existe un polynôme R de degré n tel que P est égal à RQ₁. Par hypothèse de récurrence, il existe une extension finie L de K dans laquelle la décomposition en facteurs irréductibles de R ne contienne que des polynômes de degré 1. Dans L le polynôme P est scindé.

Si ce n'est pas le cas, il existe un polynôme unitaire irréductible Q de degré strictement supérieur à 1 dans les facteurs irréductible de P et si R est le résultat de la division euclidienne de P par Q, alors P est égal à Q.R. Le polynôme Q est noté :

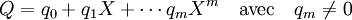
Considérons L₁, le corps des congruences de K[X] modulo le polynôme irréductible Q et χ la congruence de l'indéterminée X modulo Q. On peut écrire la congruence de Q à l'aide de χ, qui est égal à 0 modulo Q on obtient :

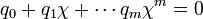
La dernière égalité signifie que l'élément χ de L₁ est une racine du polynôme Q, ou encore que dans L₁[X], le polynôme X - χ divise Q, ce qui montre l'existence d'un polynôme S à coefficients dans L₁ tel que Q = (X - χ).S, et le polynôme P s'écrit (X - χ).S.R. Le polynôme S.R à coefficients dans L₁, une extension finie de K, est de degré n, ce qui montre l'existence d'une extension L de L₁ tel que S.R soit scindé dans L. Autrement dit, le polynôme P, égal à (X - χ).S.R, est scindé dans L.

L'extension L₁ est finie dans K et l'extension L est finie dans L₁, ce qui montre que L est une extension finie de K (cf l'article extension algébrique). Ce qui termine la démonstration.