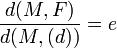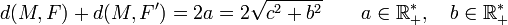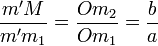Ellipse (mathématiques) - Définition

Introduction

section du cône ou projection du cercle

Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane.

On retrouve aussi, en première approximation, des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites artificiels) en orbite autour d'une étoile ou d’une autre planète. Ainsi, la Terre parcourt-elle, en première approximation, une ellipse dont le Soleil est un foyer.

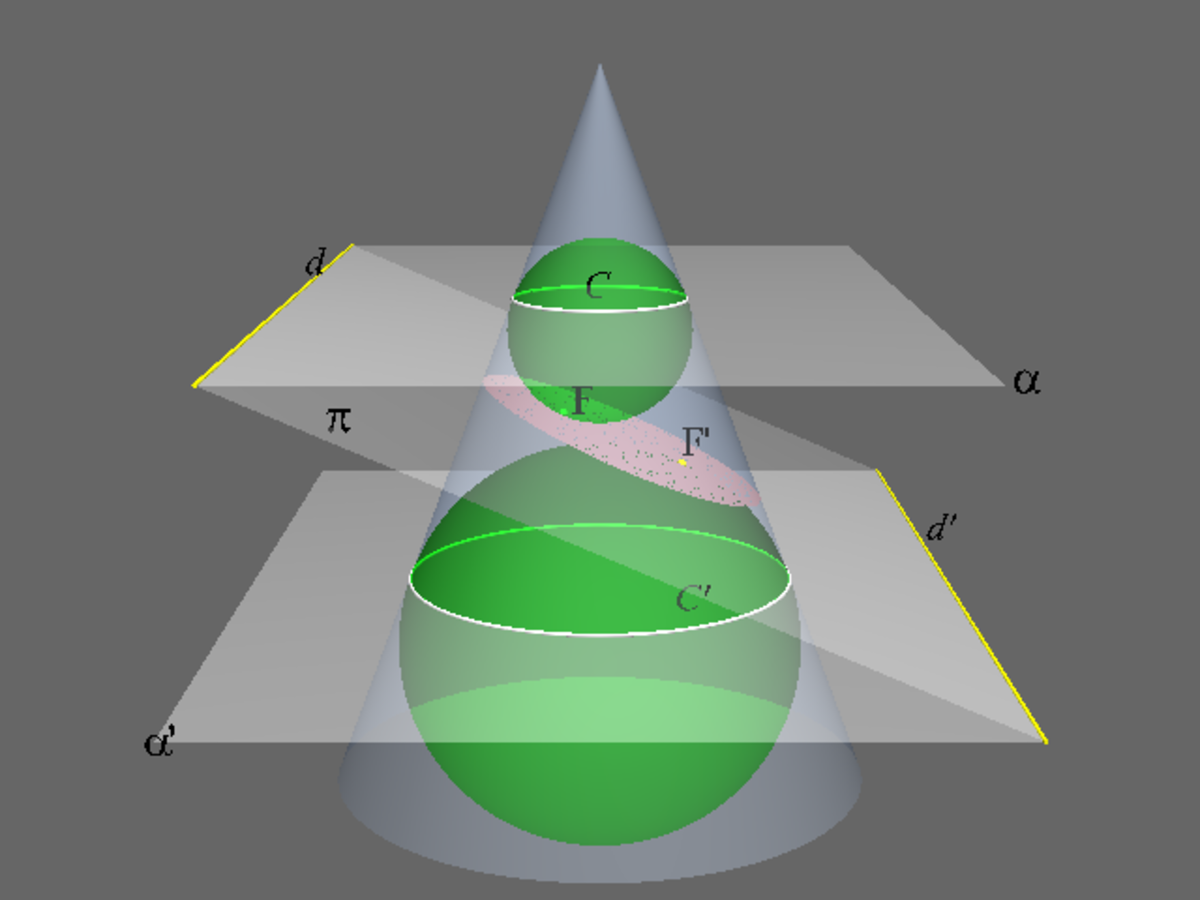
En mathématiques, une ellipse est, une courbe plane fermée obtenue par la projection d’un cercle sur un plan - à condition que la direction de la projection ne soit pas parallèle au plan du cercle - , ou par l’intersection d’un cône droit avec un plan. Il faut alors que le plan ne soit pas trop penché c'est-à-dire que l'angle entre la normale au plan et l'axe du cône soit inférieur au complémentaire de l'angle du cône (angle entre l'axe de cône et une directrice). Le cercle est considéré comme un cas particulier d’ellipse.

En géométrie, elle est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la est très simple).

Une ellipse est aussi une conique d'excentricité strictement comprise entre 0 et 1.

Définitions géométriques

Section d’un cône

L’ellipse est une courbe plane qui fait partie de la famille des coniques. Elle est obtenue par l’intersection d'un plan avec un cône de révolution lorsque ce plan traverse de part en part le cône. Le cercle est alors un cas particulier de l'ellipse (plan de coupe perpendiculaire).

Directrice et foyer

Construction d'une ellipse par foyer et directrice. Excentricité 1/2

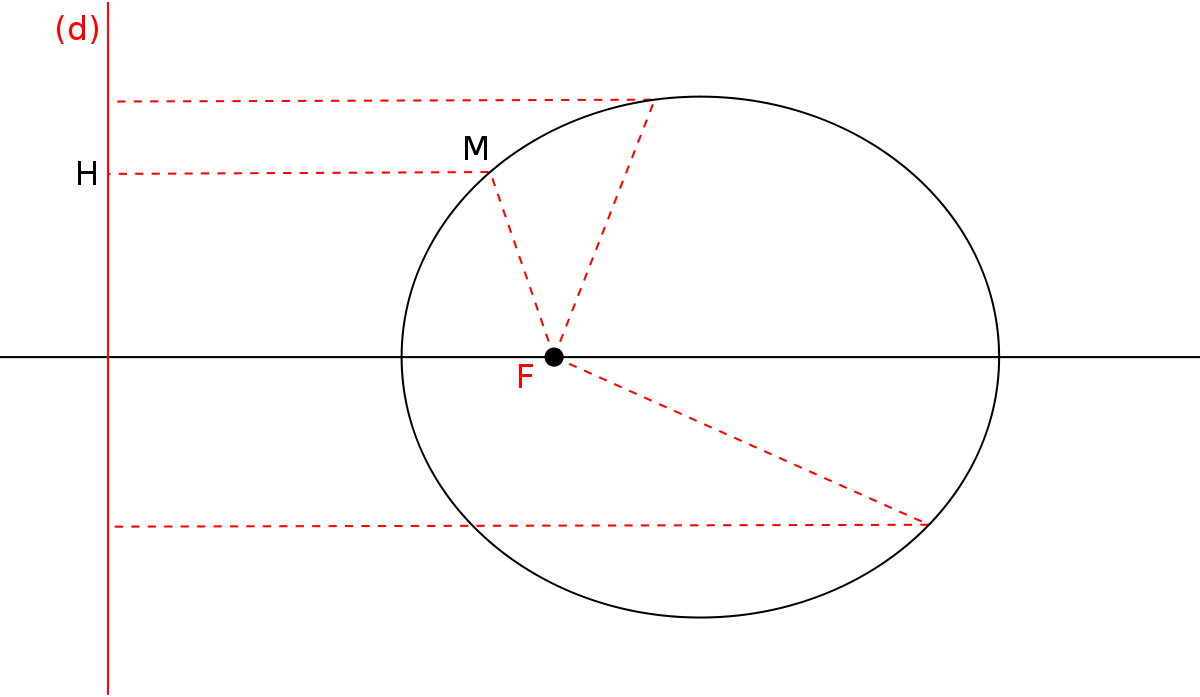
Le cadre est l'espace affine euclidien de dimension 2. Soient (d) une droite, F un point n'appartenant pas à (d), e un réel dans ]0,1[. Soit P le plan affine déterminé par (d) et F. On appelle ellipse de droite directrice (d), de foyer F d'excentricité e l'ensemble des points M du plan P vérifiant :

où d(M,F) mesure la distance du point M au point F et d(M,(d)) = d(M,H) celle de M à la droite (d).

Notons K le projeté orthogonal de F sur (d). (KF) est alors clairement un axe de symétrie de l'ellipse appelé axe focal.

Définition bifocale de l'ellipse

Construction de l'ellipse par deux foyers et une corde de longueur constante

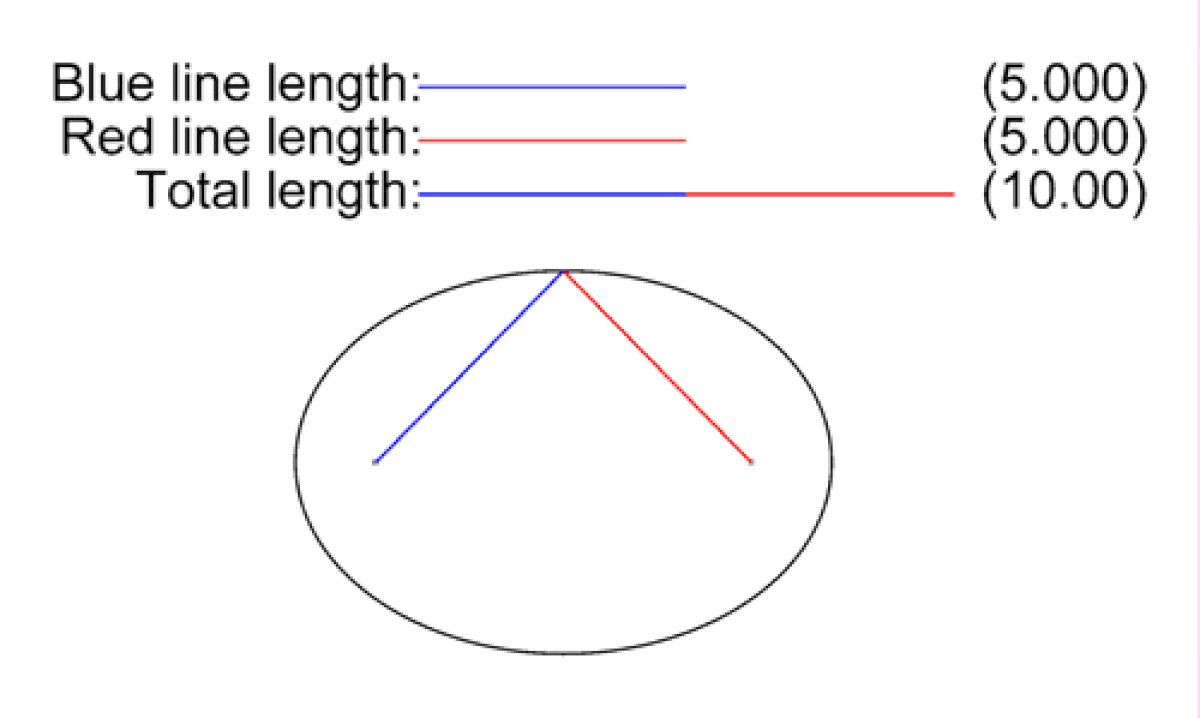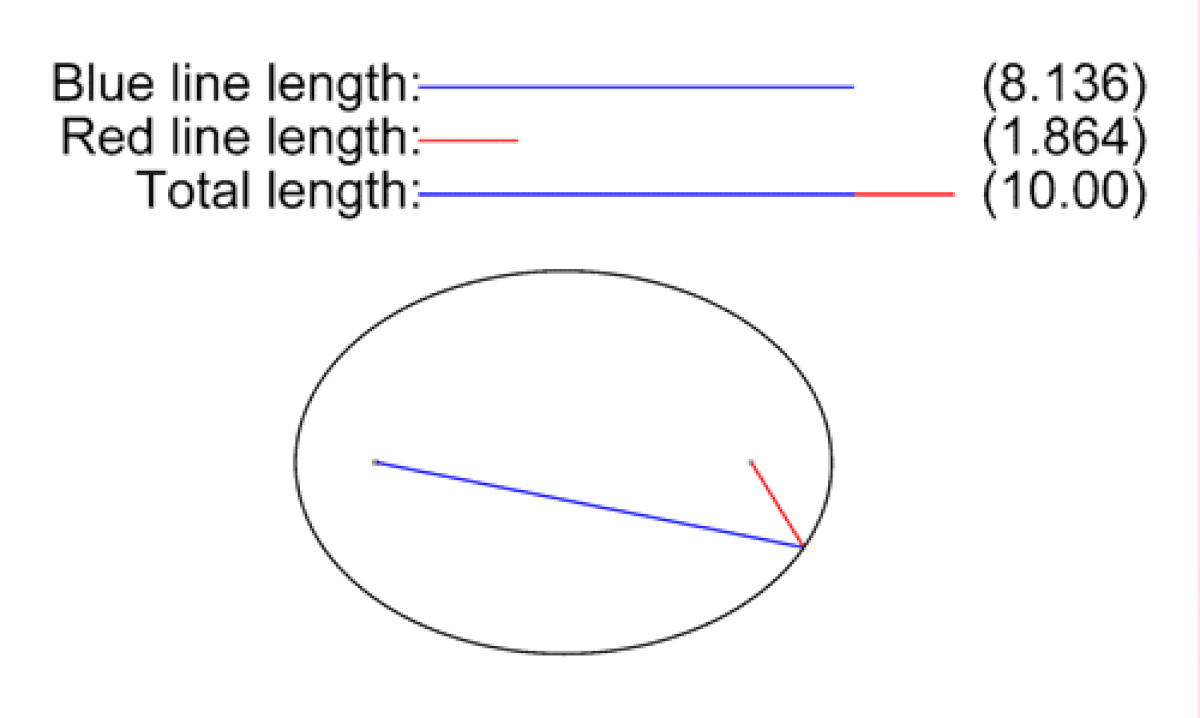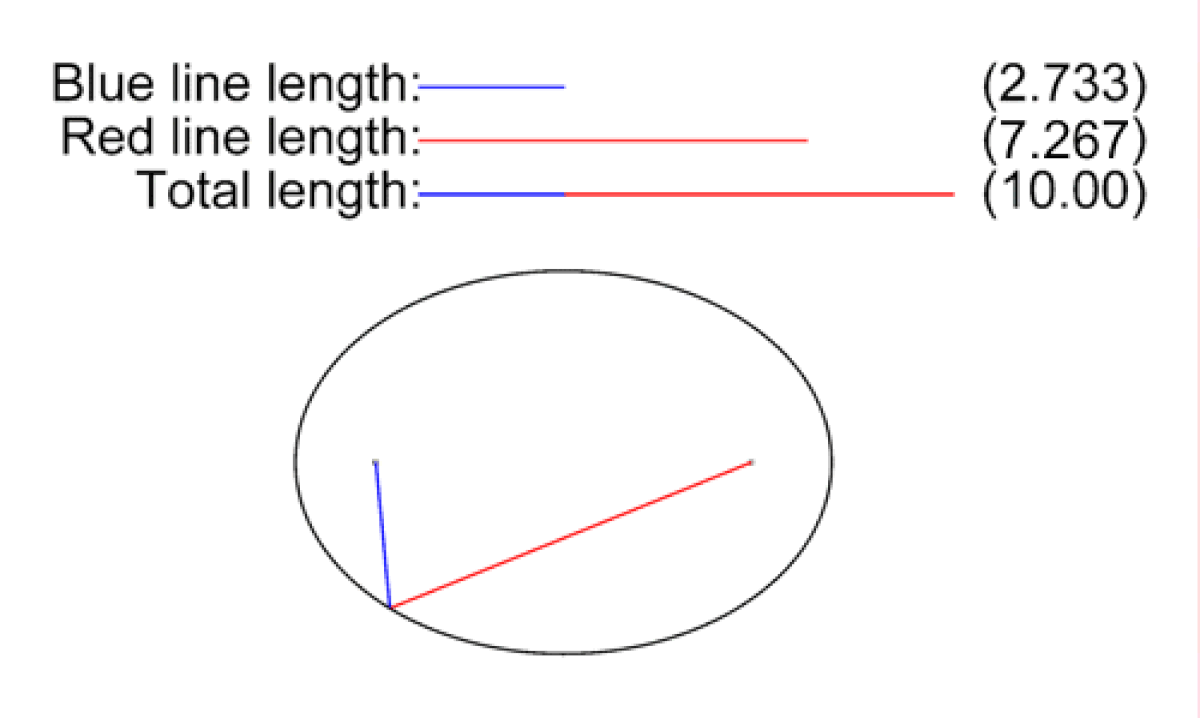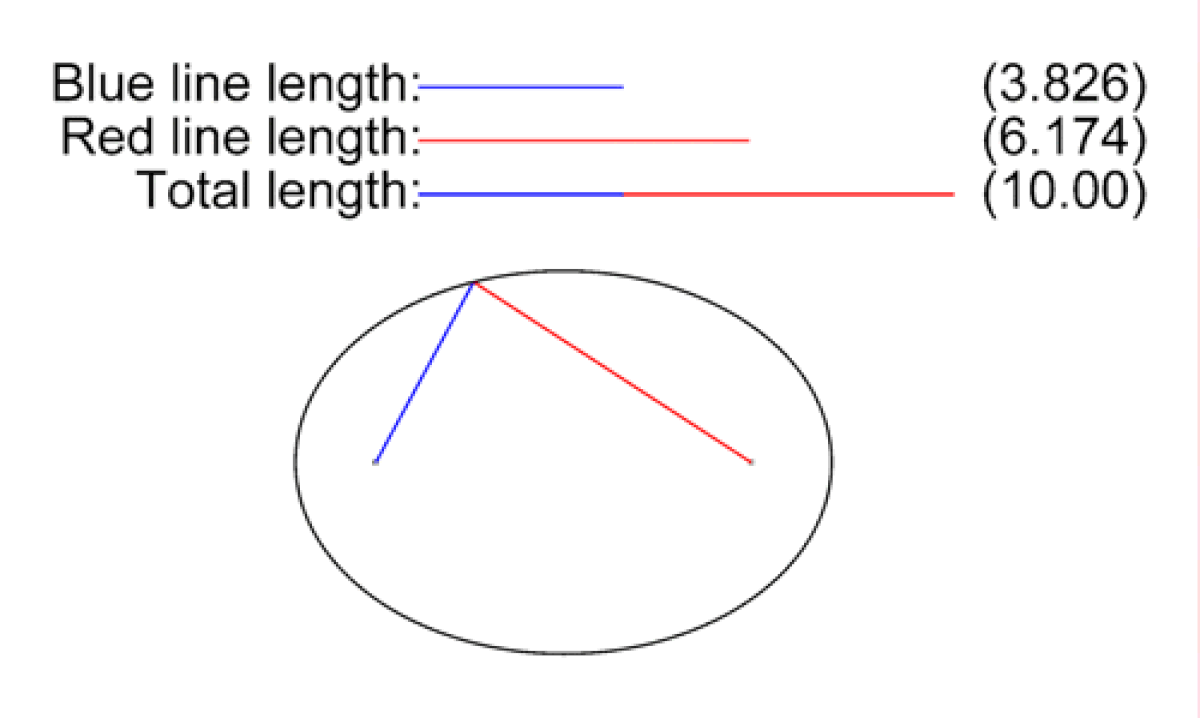
Soient F et F'' deux points distincts du plan. On appelle ellipse de foyers F et F'', l'ensemble des points M du plan vérifiant la propriété suivante :

où 2a est la longueur du grand axe, 2c = d(F,F'') et 2b est la longueur du petit axe (perpendiculaire au grand axe). Cette relation exprime que la somme des distances d'un point M aux foyers est constante et vaut la longueur du grand axe.

Image d'un cercle par une affinité

L'ellipse et les deux cercles de l'affinité

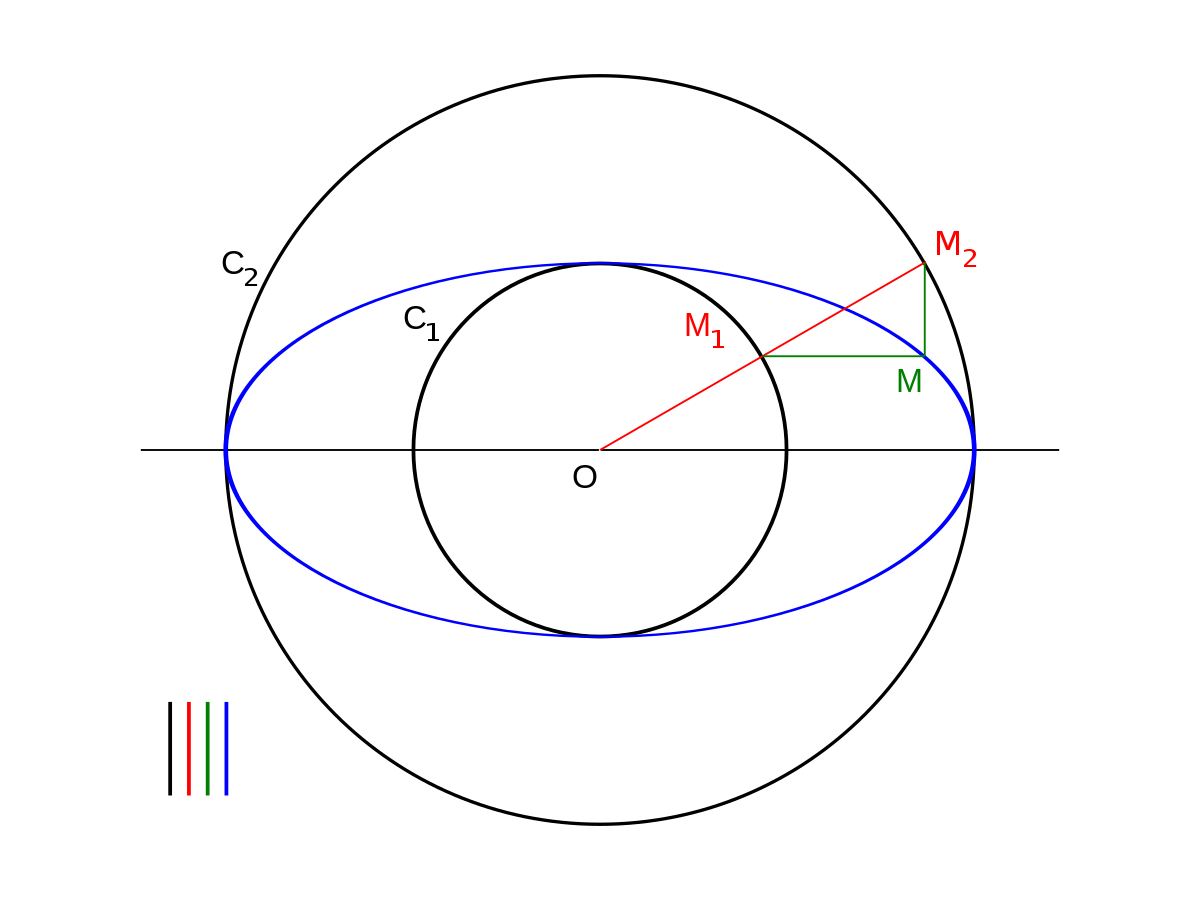
Soient (C1) un cercle de centre O et de rayon a, (C2) un cercle de centre O et de rayon b (b < a) et (xx') une droite passant par O. On appelle ellipse de centre O, de demi-grand axe a et de demi-petit axe b l'image du cercle (C1) par l'affinité d'axe (xx'), de direction perpendiculaire à (xx') et de rapport b /a.

Pour construire le point M de l'ellipse, image du point m₁ du grand cercle, on construit le point m₂ du cercle (C2) situé sur [Om₁]. On mène par m₁ une perpendiculaire à (xx') et par m₂ une parallèle à (xx'). Les droites se coupent en M. En effet, si m' est le projeté orthogonal de m₁ sur (xx'), on a, d'après le théorème de Thalès,

Construction par le cercle directeur

Ellipse et une portion de son cercle directeur

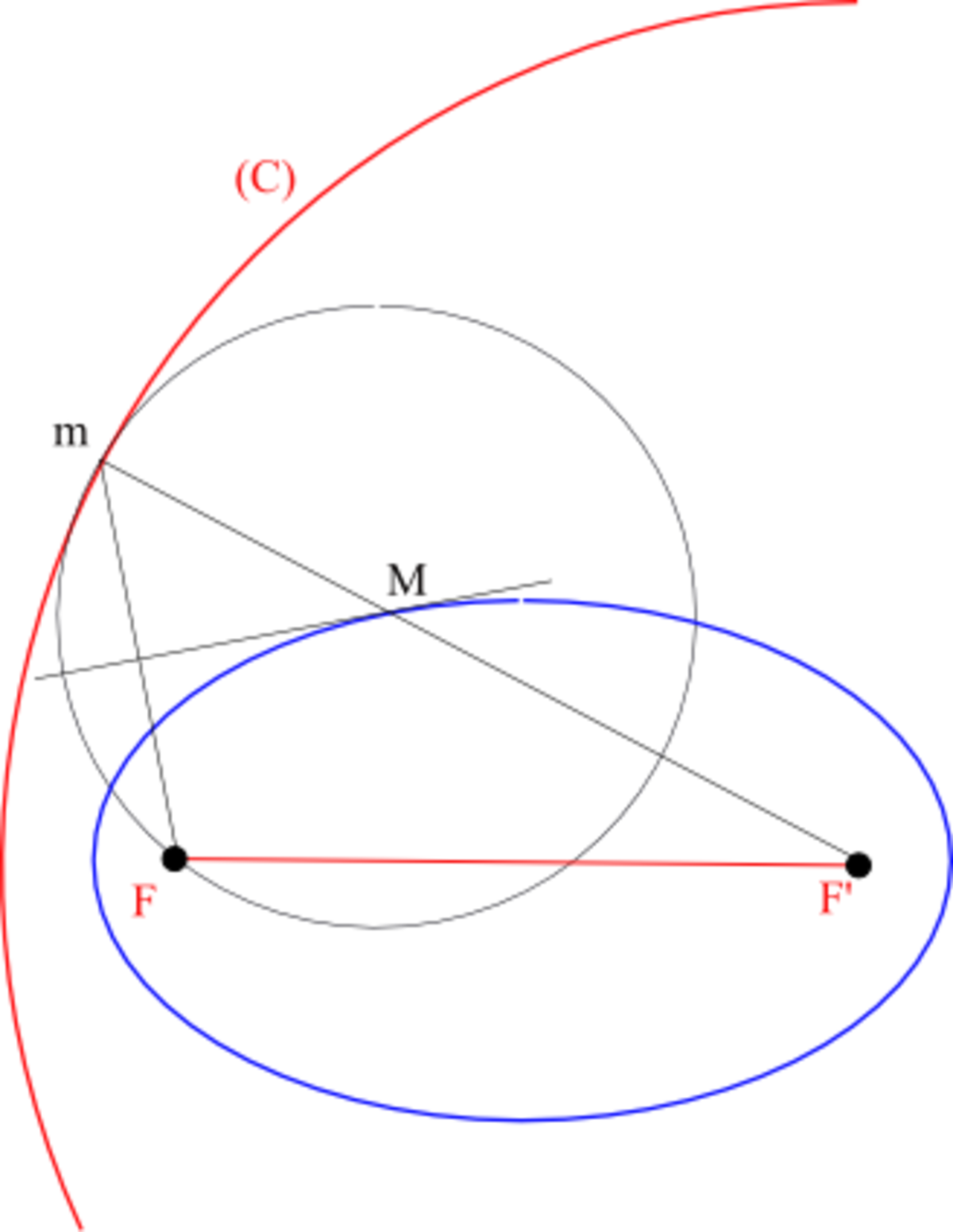
Soient F et F' deux points distincts, (C) un cercle de centre F' et de rayon 2a (2a > FF').

On appelle ellipse de cercle directeur (C) et de foyer F, l'ensemble des centres des cercles tangents à (C) et passant par F.

Pour construire le point M, centre du cercle tangent à (C) en m, on trace la médiatrice du segment [Fm], elle rencontre le rayon [F'm] en M.