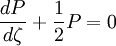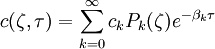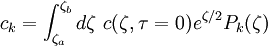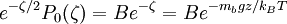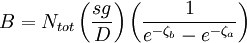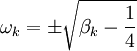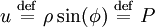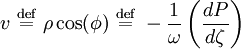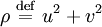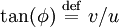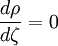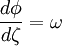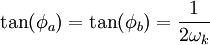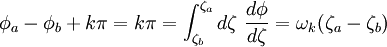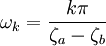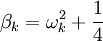Équation de Mason-Weaver - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'équation de Mason-Weaver est une équation décrivant la sédimentation et la diffusion de solutés sous l'action d'une force uniforme, typiquement un champ de pesanteur.
Expression mathématique
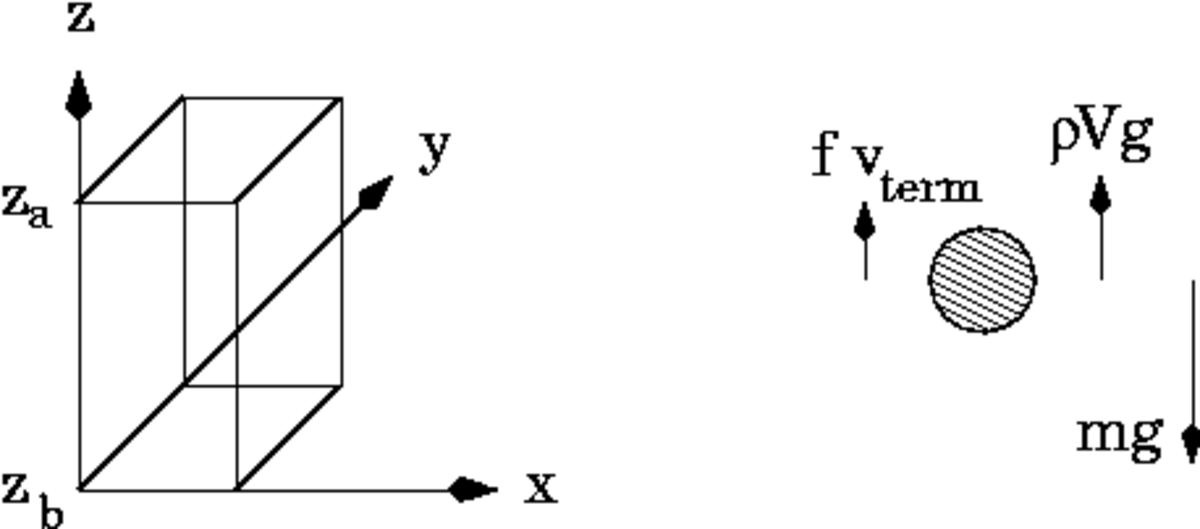
En supposant que la pesanteur est un champ orienté dans la direction z (Fig. 1), l'équation de Mason-Weaver peut s'écrire
où t est le temps, c est la concentration linéaire du soluté (moles par unité de longueur dans la direction z) et les paramètres D, s et g représentent respectivement le coefficient de diffusion du soluté, le coefficient de sédimentation et l'accélération de la pesanteur (supposée constante).
L'équation de Mason-Weaver est complétée par des conditions aux limites. Si la cellule est supposée rectangulaire et aligné sur un syustème de coordonnées cartésiennes (Figure 1) on a
au sommet et au fond de la cellule notée respectivement za and zb (Fig. 1). Ces conditions aux limites correspondent au fait que physiquement il est impossible à un soluté de passer à travers les parois de la cellule et que le flux doit donc y être nul. De même le flux sur les parois latérales doit être nul. En conséquence la quantité totale de solutés contenus dans la cellule
est conservée, i.e. dNtot / dt = 0.
L'équation de Mason-Weaver sans dimension
Les paramètres D, s et g déterminent une longueur caractéristique z0
et un temps caractéristique t0
En définissant les grandeurs sans dimension
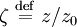
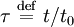
soumise aux conditions aux limites
au sommet et au fond de la cellule, respectivement ζa et ζb.
Obtention de l'équation de Mason-Weaver
Une particule de masse m se déplaçant à la vitesse verticale v est soumise à trois forces (Fig. 1) : la force de traînée fv, son poids mg et la poussée d'Archimède ρVg, où g est l'accélération de la pesanteur, V est le volume de la particule de soluté et ρ est la masse volumique du solvant. À l'équilibre mécanique (typiquement atteint en 10 ns pour des solutés moléculaires), les particules atteignent une vitesse limite vterm pour laquelle les trois forcent se compensent.
Étant donné que le volume V est égal à la masse m de la particule multipliée par son volume massique
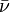
où mb est la masse apparente du soluté compte tenu de la poussée d'Archimède.
On peut définir le coefficient de sédimentation de Mason-Weaver
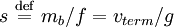
-
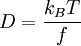
la rapport s sur D est égal à
où kB est la constante de Boltzmann et T est la température temperature en kelvin.
Le flux J en un point quelconque est donné par
le premier terme décrit le flux dû à la diffusion de la matière sous l'effet d'un gradient de concentration, tandis que le second terme décrit le flux convectif dû à la vitesse moyenne vterm des particules. Un flux net positif en dehors d'un petit volume produit une diminution locale de la concentration dans ce volume :
En remplaçant J par son expression dans l'équation précédente on obtient l'équation de Mason-Weaver
Solution de l'équation de Mason-Weaver
Cette équation peut être résolue par une méthode de séparation des variables. En posant
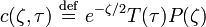
où les valeurs possibles de β sont définies par les conditions aux limites
aux frontières supérieure et inférieure ζa et ζb respectivement. Puisque l'équation en T admet les solutions T(τ) = T0e − βτ où T0 est une constante la résolution de l'équation de Mason-Weaver se réduit à trouver la fonction P(ζ).
Les équations différentielles ordinaires pour P et ses conditions satisfont les critères de la théorie de Sturm-Liouville ce qui amène à plusieurs conclusions. Tout d'abord il existe un ensemble orthonormé de fonctions propres Pk(ζ) qui est solution des équations différentielles et satisfait les condition aux limites. De plus les valeurs propres correspondantes βk sont réelles, limitées inférieurement par la valeur propre β0 et croissent asymptotiquement comme k2 où l'entier naturel k est le rang de la fonction propre. Dans le cas présent la plus petite valeur propre est zéro, correspondant à l'équilibre. Enfin, les fonctions propres forment un ensemble complet ; toute solution pour c(ζ,τ) peut être exprimée comme une combinaison linéaire des fonctions propres
où ck sont des coefficients constants déterminés à partir de la distribution initiale c(ζ,τ = 0)
À l'équilibre par définition β = 0 et la distribution de concentration à l'équilibre est :
ce qui est en accord avec la distribution de Boltzmann.
Les fonctions P0(ζ) sont solutions des équations différentielles et satisfont aux conditions aux limites pour toutes les valeurs de ζ (ce que l'on peut vérifier par substitution) et la constante B peut-être déterminée à partir de la quantité totale de soluté.
Pour trouver les valeurs propres hors équilibre βk, nous procédons comme suit. L'équation en P équation a la forme d'un oscillateur harmonique simple de solutions
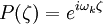
Suivant la valeur de βk, ωk est soit purement réel (
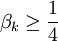
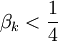
- P(ζ) = Acosωkζ + Bsinωkζ
où A et B sont des constantes et ω est un réel strictement positif.
En introduisant l'amplitude de l'oscillateur ρ et la phase φ comme nouvelles variables,
l'équation du second degré en P est factorisée en deux équations du premier degré
De façon remarquable les conditions aux limites obtenues sont indépendantes de ρ ainsi que des points extrêmes ζa et ζb
En conséquence on obtient l'équation
donnant une solution exacte pour les fréquences ωk
Les fréquences propres ωk sont positives puisque ζa > ζb et consistent en un jeu d'harmoniques e la fréquence fondamentale
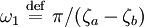
Prises ensembles les composantes de la solution hors équilibre correspondent à une décomposition en séries de Fourier de la distribution de concentration initiale c(ζ,τ = 0) pondérée par les eζ / 2. Chaque composante de Fourier décroît comme indépendamment comme
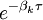
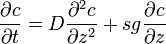
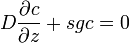
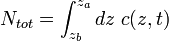
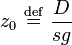
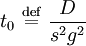
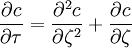
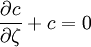
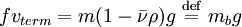
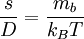

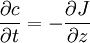
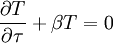
![\frac{\partial^{2} P}{\partial \zeta^{2}} + \left[ \beta - \frac{1}{4} \right] P = 0](https://static.techno-science.net/illustration/Definitions/autres/7/7362c04dd9333370d3b69af7b4106b8c_1fdfae1e75fef3740119157f9a7bd878.png)