Espace euclidien - Définition

Construction d'espaces euclidiens

Comme fréquemment en algèbre, la donnée d'espaces euclidiens permet d'en construire de nouveaux.

Sous-espace, espace produit

Si F est un sous-espace vectoriel d'un espace euclidien, alors la restriction du produit scalaire induit une structure d'espace vectoriel euclidien sur F.

Si E₁ et E₂ sont deux espaces euclidiens, alors leur produit dispose d'une structure euclidienne. Le produit scalaire est donné par la formule :

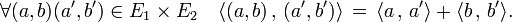
Espace quotient

La nature des projecteurs orthogonaux permet d'attribuer un produit scalaire à un quotient d'un espace euclidien. La norme d'une classe de x de l'ensemble E/F correspond à la distance entre un représentant de la classe et F. Si représente la classe de x, alors le produit scalaire <. , . >_E/F sur E/F est défini par :

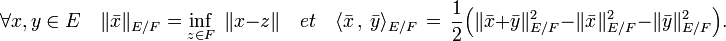
Il existe une isométrie canonique entre le supplémentaire orthogonal de F (muni de la structure d'espace euclidien en tant que sous-espace vectoriel), et le quotient E/F, muni de la structure d'espace euclidien décrite précédemment, qui à tout élément de ce supplémentaire orthogonal associe sa classe dans E/F. Ceci provient de l'identité, suivante, où p est le projecteur orthogonal de direction F :

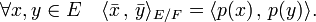
Produit tensoriel

Soient E₁ et E₂ deux espaces euclidiens de dimensions respectives n₁ et n₂, s'ils sont identifiés à leurs duaux à l'aide de l'isomorphisme canonique φ, l' espace tensoriel E₁E₂ s'identifie à l'ensemble des formes bilinéaires de E₁xE₂. Le produit tensoriel est une application bilinéaire de E₁xE₂ dans E₁E₂ définie par :

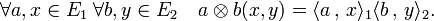
L'image de E₁xE₂ par le produit tensoriel est une partie génératrice de E₁E₂, il suffit donc de définir le produit scalaire sur cette image pour le définir sur tout l'espace. Le produit scalaire est alors défini par l'égalité suivante :

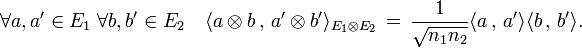
Endomorphisme

Si E₁ et E₂ sont confondus, le produit scalaire précédent est celui de L₂(E). L'isomorphisme canonique ψ₁ de L(E) dans L₂(E) permet de munir L(E) d'une structure d'espace euclidien :

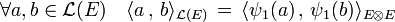
Le choix de l'isomorphisme ψ₁ ou ψ₂, définis dans le paragraphe Espace dual et forme bilinéaire, est arbitraire, ils amènent tous deux au même produit scalaire. Ce produit scalaire de L(E) confère aux deux isomorphismes le caractère d'isométrie.

L'adjoint permet une expression plus simple du produit scalaire sur L(E). le produit scalaire de deux endomorphismes a et b correspond à la trace de l'endomorphisme adjoint de b composée avec a :

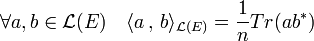
Pour ce produit scalaire, les endomorphismes autoadjoints et antisymétriques forment deux sous-espaces orthogonaux en somme directe et le groupe orthogonal est inclus dans la sphère unité.

Généralisations

Il existe plusieurs généralisations des espaces euclidiens. En choisissant comme corps de base le corps des nombres complexes, on obtient la notion d'espace hermitien. De tels espaces admettent une théorie analogue, au prix d'adaptations naturelles : les résultats présentés dans cet article restent intégralement vérifiés pour ces espaces.

En dimension infinie, une définition analogue (existence d'un produit scalaire ou hermitien) amène d'abord à la notion de préhilbertien, dans le cas réel et dans le cas complexe. Le caractère complet n'est pas vérifié en général. Un espace préhilbertien, complet pour la topologie d'espace métrique induite par la norme préhilbertienne, est appelé espace de Hilbert. Les espaces de Hilbert font l'objet d'une riche théorie, et sont des objets de base en analyse fonctionnelle.

Une géométrie euclidienne est définie par un espace vectoriel et une forme bilinéaire particulière (définie positive). Travailler avec certaines autres formes bilinéaires permet d'obtenir d'autres géométries, par exemple la géométrie symplectique.

Pour d'autres corps de base que les réels ou les complexes, la notion de forme bilinéaire définie positive n'est en général pas pertinente, car le corps n'est pas ordonné. On remplace généralement cette hypothèse par le fait que la forme est non dégénérée, c'est-à-dire qu'il n'existe pas de vecteur non nul orthogonal à tout l'espace. Une telle structure est utilisée, par exemple pour la géométrie sur les groupes finis. Les groupes orthogonaux sur des espaces vectoriels de dimension finie sur les corps finis fournissent notamment des familles infinies de groupes simples.

La Wikiversité possède des cours sur « Espace euclidien ».