Figure de la Terre - Définition
La liste des auteurs de cet article est disponible ici.
Figure géodésique de référence : ellipsoïde normal, ou « sphéroïde »
Pour servir de base aux mesures géodésiques la surface topographique n'est pas appropriée, car elle n'est pas de niveau ; or, la plupart des appareils géodésiques doivent être mis en station, c'est–à-dire se repèrent par rapport à la verticale de l'endroit où l'on effectue les mesures. Or, la verticale du lieu est normale à la surface de niveau en ce point. Comme standard de référence pour étudier la figure de la Terre et le champ de pesanteur on adopte donc un ellipsoïde de révolution auquel on attache la propriété physique d'être une surface équipotentielle pour la pesanteur. Une telle surface de niveau ellipsoïdale est souvent appelée « sphéroïde normal ». Dans cette appellation, on emploie le mot « sphéroïde » au sens restreint d'un ellipsoïde à symétrie axiale ; dans son acception générale, ce mot désigne une figure géométrique vaguement sphérique, et peut s'appliquer tout aussi bien au géoïde envisagé plus bas.
D'un point de vue géométrique, un ellipsoïde de référence est complètement défini si nous fixons, outre son orientation dans l'espace, deux quelconques parmi les trois éléments suivants :
- a, le demi-grand axe de la section elliptique dans un plan passant par l'axe polaire : a désigne, en pratique, le rayon équatorial de la Terre ;
- c, le demi-petit axe, qui est, en pratique, équivalent au rayon polaire de la Terre ;
- f, l'aplatissement géométrique, défini par f = a−c⁄a.
Lorsqu'on peut se limiter à une précision de l'ordre de 100 à 150 mètres sur la détermination des altitudes rapportées au niveau moyen de la mer, une telle surface de niveau en forme d'ellipsoïde de révolution fait bien l'affaire, à condition de bien ajuster les paramètres représentant le rayon équatorial et l'aplatissement géométrique. Même si un ellipsoïde de référence est une surface de niveau par définition, il convient de ne pas lui attacher de signification physique. En particulier, dans sa définition on ne spécifie pas la distribution des masses en son intérieur, même si l'on stipule que sa masse totale M doit être celle de la Terre. Par conséquent, le potentiel gravifique n'est pas défini à l'intérieur de l'ellipsoïde. Néanmoins, pour que l'ellipsoïde de référence puisse se prêter à des calculs gravimétriques, sa propriété d'être une surface équipotentielle pour la pesanteur est essentielle.
Potentiel de pesanteur du sphéroïde normal
Une surface de niveau est une surface sur laquelle la somme du potentiel gravifique V et du potentiel axifuge Z reste constante. On appelle cette somme V + Z le potentiel de pesanteur et on le désigne par U. Ainsi, l'équation d'une surface de niveau s'écrit
En considérant la « constante » Uo comme un paramètre, toute une famille de telles surfaces de niveau est ainsi définie. Ces surfaces s'emboîtent sans se recouper. Dans la suite, partout où c'est nécessaire, un astérisque distinguera les quantités relatives à l'ellipsoïde. Ainsi, V* est le potentiel de gravité normale, et U* = V* + Z est le « potentiel de pesanteur normale », ou simplement le potentiel normal. Le potentiel de pesanteur actuel de la Terre, U = V + Z, est appelé « géopotentiel ». Les constantes particulières définissant le géoïde et l'ellipsoïde de référence sont dénotées Uo et Uo*, respectivement.
Potentiel axifuge
Pour un point matériel quelconque attaché à la Terre, la rotation de celle-ci produit une accélération axifuge perpendiculaire à l'axe de rotation. En effet, si (x1,x2,x3) sont les coordonnées cartésiennes du point matériel par rapport à des axes fixes dont l'origine O est le centre de la Terre, Ox3 étant orienté le long de l'axe polaire, les composantes de l'accélération axifuge du point sont ( − ω2x1, − ω2x2,0). La lettre grecque ω est utilisée conventionnellement pour désigner la vitesse angulaire de rotation de la Terre. Dans le système géodésique de référence international utilisé actuellement elle possède la valeur
(plus précisément, 7,292 115 146 706 4 « nominal »)
Or, les composantes de l'accélération d'un point matériel se mouvant librement dans un champ de force gravifique sont égales aux composantes du champ de force gravifique par unité de masse, c'est-à-dire égales à –∂V⁄∂xi, i∈{1,2,3}. Dans un repère tournant avec la Terre, les composantes de l'accélération sont égales aux différences entre celles d'une particule gravitant librement et celles d'une particule qui coïncide initialement avec elle, mais qui est attachée à la Terre. Ce sont les composantes gi de la pesanteur. On a :
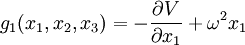
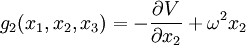
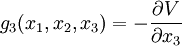
Dès lors, nous définissons le potentiel axifuge par l'expression
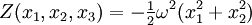
Potentiel de gravité extérieur d'un sphéroïde normal
Le problème consiste donc à déterminer V*, sur la surface de niveau U* = Uo* et à l'extérieur de l'ellipsoïde dans tout l'espace, en termes de l'aplatissement f, et de comparer ensuite l'expression obtenue ainsi avec l'expression du potentiel gravifique extérieur V déterminé par la géodésie spatiale au moyen de données satellitaires afin d'obtenir un ajustement pour f. Une solution pour la première partie de ce problème, à savoir l'obtention d'une expression pour le champ gravifique externe d'un sphéroïde normal, fut donnée en 1894 par le géodésien italien Pizzetti
Ce dernier résolut l'équation de Laplace qui régit le potentiel newtonien extérieur dans un système de coordonnées ellipsoïdales qui est directement adapté à une surface-frontière sphéroïdale, et obtint une formule fermée qui peut être développée en série de puissances de f. La précision des mesures géodésiques globales est telle que les termes en f et f2 doivent être retenus, mais que les termes d'ordre f3 et plus petits peuvent être négligés en pratique ; cependant, la considération de termes d'ordre supérieur au second ne pose aucun problème. Ainsi, un développement de V* incluant les termes en f3 a été publié par Cook en 1959 et par Hirvonen en 1960. Des comptes-rendus concernant la théorie de Pizzetti se trouvent dans de nombreux ouvrages. Cependant, dans les applications pratiques il est en général plus approprié d'employer un système de coordonnées sphériques plutôt que de coordonnées ellipsoïdales et de procéder à un développement en série d'harmoniques sphériques, nonobstant le fait de la difficulté mathématique engendrée par des problèmes de convergence lorsqu'on utilise un système de coordonnées sphériques polaires pour traiter une situation de géométrie non-sphérique.
Dans le cas présent, on peut prouver que le développement en harmoniques sphériques du potentiel gravifique extérieur d'un ellipsoïde de niveau converge sur la surface de l'ellipsoïde, et même bien en dessous de cette surface jusqu'à la surface sphérique homocentrique passant par les foyers de l'ellipsoïde. Il devrait être clair, toutefois, que le prolongement analytique du potentiel extérieur à l'intérieur de l'ellipsoïde ne peut pas représenter de façon appropriée le potentiel interieur, parce que la solution pour le potentiel extérieur n'est pas une solution de l'équation de Poisson. La démonstration du théorème de Moritz peut être esquissée de la manière suivante : À cause de la symétrie de révolution du sphéroïde normal, le développement formel de V* en une série d'harmoniques sphériques contiendra seulement des termes zonaux, et à cause de la symétrie par rapport au plan équatorial (théorème de Lichtenstein), il y aura seulement des termes pairs. Dès lors, la série formelle peut se mettre sous la forme
![V^*(x,\theta) = - \frac{GM}{a} \left[\frac ax - \sum_{n=1}^\infty \left(\frac{a}{x}\right)^{2n+1} J_{2n}^* P_{2n}(\cos \theta)\right]](https://static.techno-science.net/illustration/Definitions/autres/6/695fec3104de95df2c2ca72564ee1bc5_8878383d29dd61c62f1c2dd6559fd5c1.png)