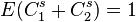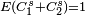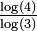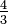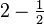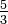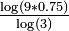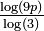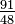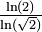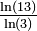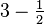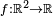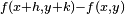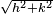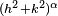Liste de fractales par dimension de Hausdorff - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Fractales aléatoires et naturelles
| δ (val. exacte) | δ (val. approchée) | Nom | Illustration | Remarques |
|---|---|---|---|---|
| 1/2 | 0.5 | Zeros du graphe d'une fonction brownienne (Processus de Wiener) |
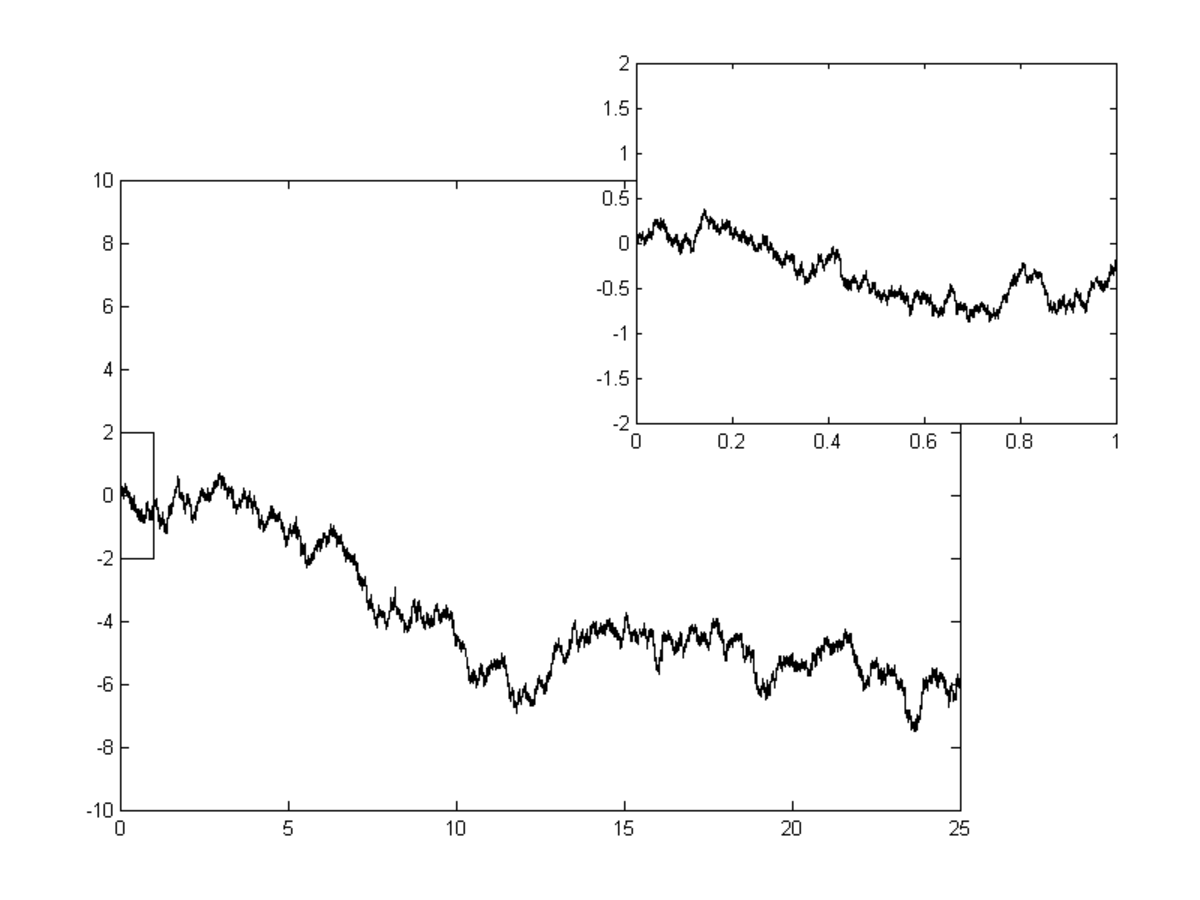
| Les zéros du graphe d'une fonction brownienne constituent un ensemble nulle part dense, de mesure de Lebesgue 0, avec une structure fractale. |
| Solution de
| 0.7499 | Ensemble de Cantor aléatoire 50% / 30% |
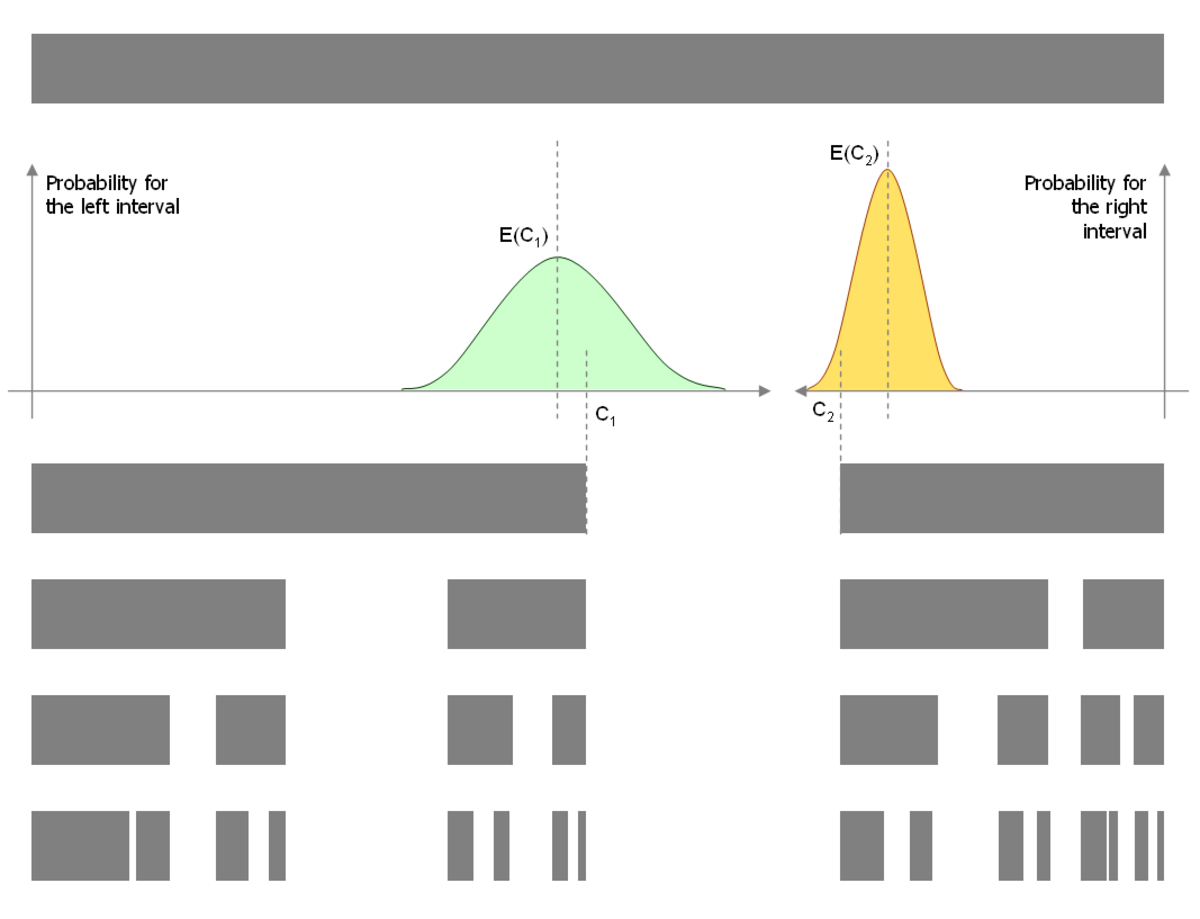
| A chaque itération, la longueur de l'intervalle de gauche est définie par une variable aléatoire C1: un pourcentage variable de la longueur du segment d'origine. Idem pour l'intervalle de droite, avec pour autre variable aléatoire C2. Sa dimension de Hausdorff s satisfait alors l'équation :
|
| Mesuré | 1,05 | Chromosome humain no 22 |
| Voir référence pour les détails de la méthode de calcul. |
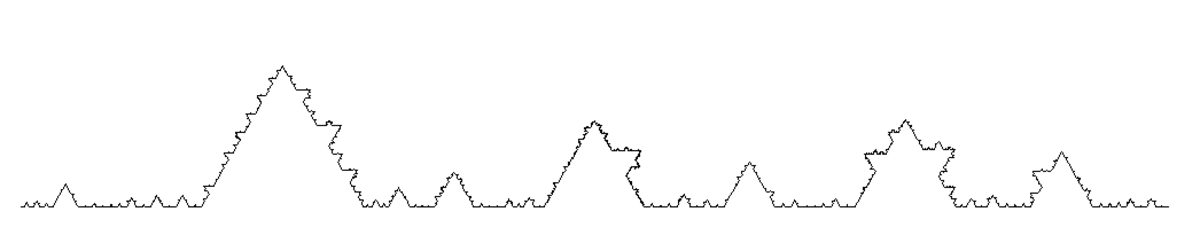
| Solution de s + 1 = 12 * 2 − (s + 1) − 6 * 3 − (s + 1) | 1.144… | Courbe de Koch avec intervalle aléatoire |
| La longueur de l'intervalle médian est une variable aléatoire à distribution uniforme dans (0;1/3). |
| mesuré | 1,24 | Côte de Grande-Bretagne |
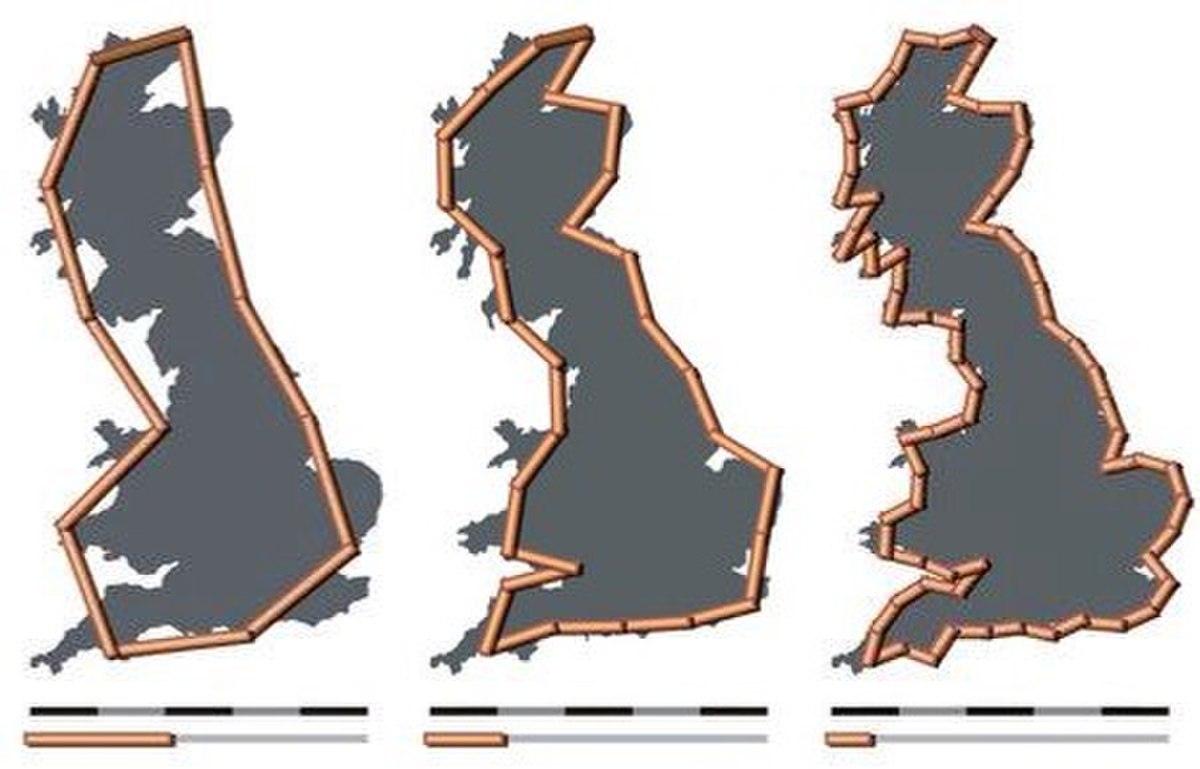
| Dimension fractale de la côte ouest de Grande-Bretagne, mesurée par Lewis Fry Richardson et cité par Benoît Mandelbrot. |
|
| 1.2619 | Courbe de Koch avec orientation aléatoire |

| On introduit ici un élément de hasard qui n'affecte pas la dimension en choisissant aléatoirement, à chaque itération, de placer le triangle équilatéral au-dessus ou en dessous de la courbe. |
|
| 1,33 | Frontière du mouvement brownien |
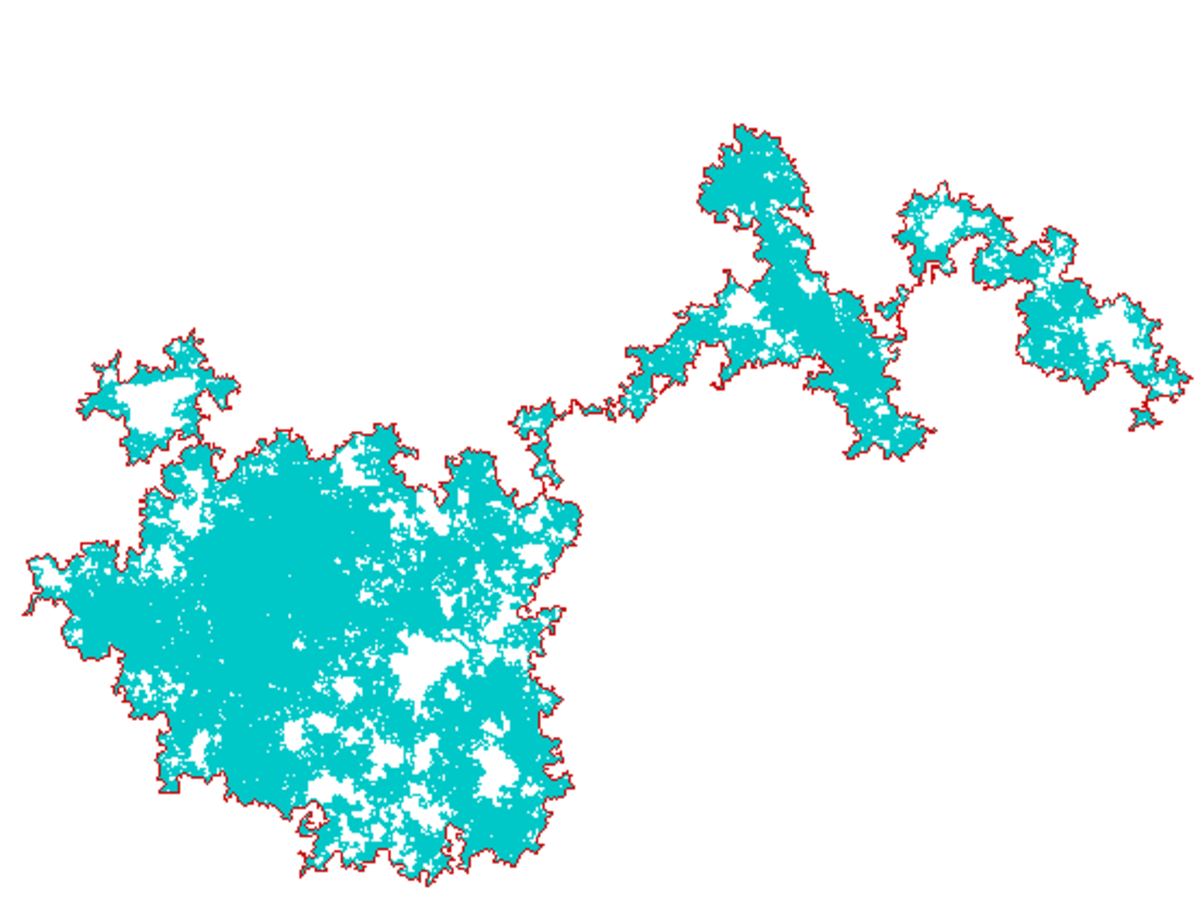
| |
|
| 1,33 | Polymère en deux dimensions | Similaire au mouvement brownien sans auto-intersection. | |
|
| 1,33 | Front de percolation, front de corrosion en deux dimensions |

| Dimension fractale du front de percolation par invasion au seuil de percolation (59,3%). C'est également la dimension fractale du front de corrosion. |
| 1,40 | Agrégat d'agrégats en deux dimensions | Des agrégats se combinent progressivement en un agrégat unique de dimension 1,4. | ||
|
| 1.5 | Graphe d'une fonction Brownienne (Processus de Wiener) |

| Graphe d'une fonction f telle que, pour tout couple de réels positifs x et x + h, la différence de leurs images f(x + h) − f(x) suit une distribution gaussienne centrée de variance = h. Généralisation : Une fonction fractionnelle Brownienne d'index α suit la même définition mais avec une variance = h2α, dans ce cas, la dimension de Hausdorff de son graphe = 2 − α. |
| Mesuré | 1,52 | Côte de Norvège |
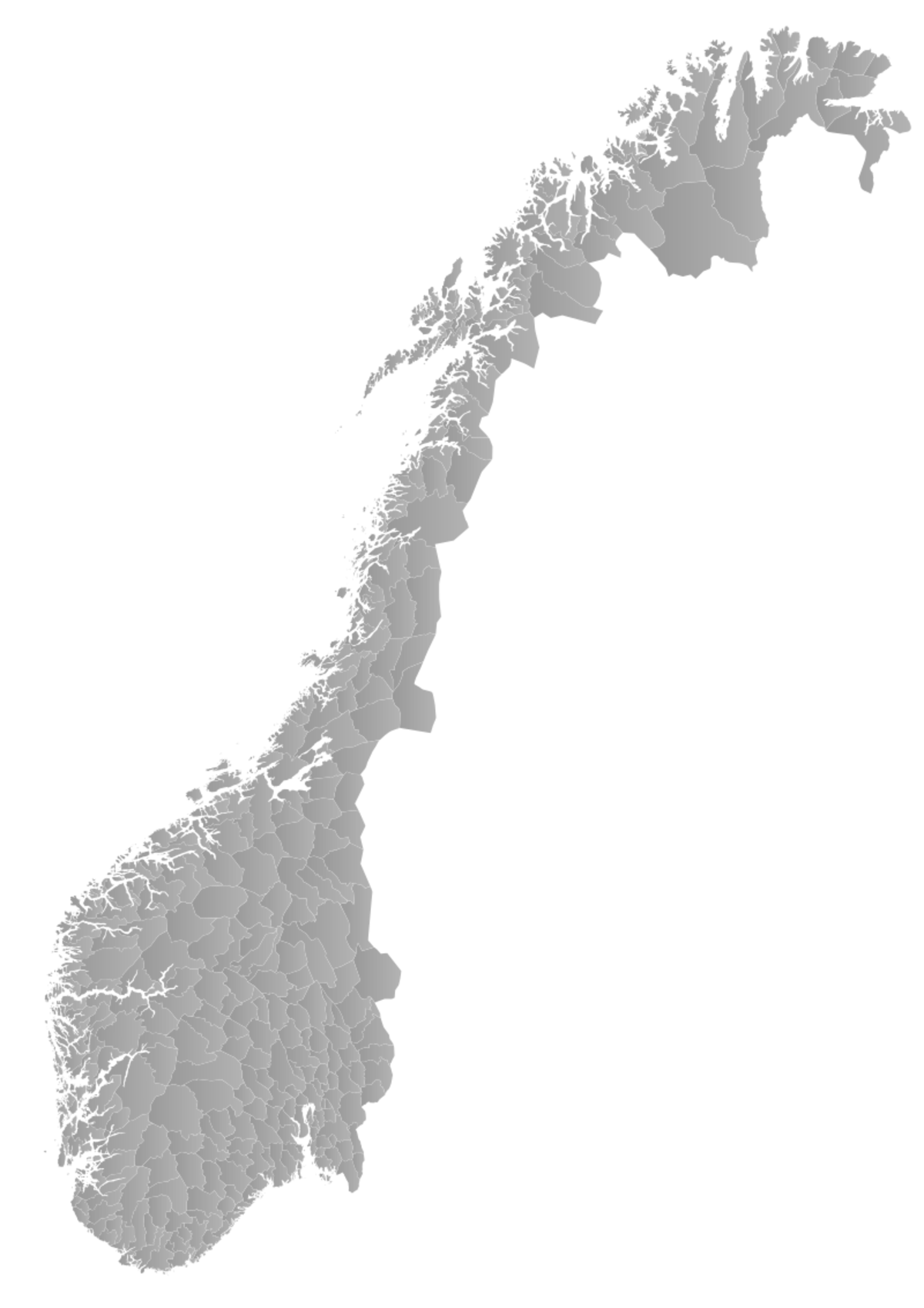
| Cf J. Feder. |
| Mesuré | 1,55 | Marche aléatoire sans intersection |

| Marche aléatoire dans un réseau carré sans auto-intersection, avec algorithme de retour arrière pour évitement des impasses. |
|
| 1,66 | Polymère en trois dimensions | Similaire au mouvement brownien dans un réseau cubique, mais sans auto-intersection. | |
| 1,70 | Agrégat par diffusion en deux dimensions | En deux dimensions, des particules forment progressivement par diffusion un agrégat de dimension 1,70. | ||
|
| 1.7381 | Percolation fractale à 75% de probabilité |

| Le modèle de percolation fractale est construit par le remplacement progressif de chaque carré par une grille de 3x3 dans laquelle est placée une collection aléatoire de sous-carrés, chaque sous-carré ayant une probabilité p d'être retenu. La dimension de Hausdorff "presque certaine" égale
|
| 7/4 | 1,75 | Frontière d'un amas de percolation en deux dimensions |

| La frontière d'un amas de percolation peut également être simulée par une marche générant spécifiquement cette frontière ou en utilisant l'évolution de Schramm-Loewner. |
|
| 1,8958 | Amas de percolation en deux dimensions |

| Sous le seuil de percolation (59,3%), l'amas de percolation par invasion couvre une surface de dimension fractale 91/48,. Au-delà du seuil, l'amas est infini et 91/48 devient la dimension fractale des « clairières ». |
|
| 2 | Mouvement brownien |

| Modélisé par la marche aléatoire. La dimension de Hausdorff reste égale 2 dans toutes les dimensions supérieures ou égales à 2. |
| Mesuré | Environ 2 | Distribution des amas de galaxies |

| Mesuré à partir des résultats 2005 du Sloan Digital Sky Survey. Voir référence |
|
| 2,33 | Surface du chou-fleur |

| Chaque branche porte environ 13 branches 3 fois plus courtes. |
| 2,4 ± 0,2 | Boule de papier froissé |

| Le diamètre de la boule de papier froissé, élevé à une puissance non entière comprise entre 2 et 3 est approximativement proportionnel à la surface de papier utilisé. Les plis se forment à toutes les échelles. | |
| 2,50 | Agrégat par diffusion en trois dimensions | En trois dimensions, des particules forment progressivement par diffusion un agrégat de dimension 2,5. | ||
| 2.50 | Figure de Lichtenberg |

| Les décharges electriques arborescentes, dites figures de Lichtenberg, croissent à la manière d'une diffusion par agrégation. | |
|
| 2.5 | surface Brownienne |
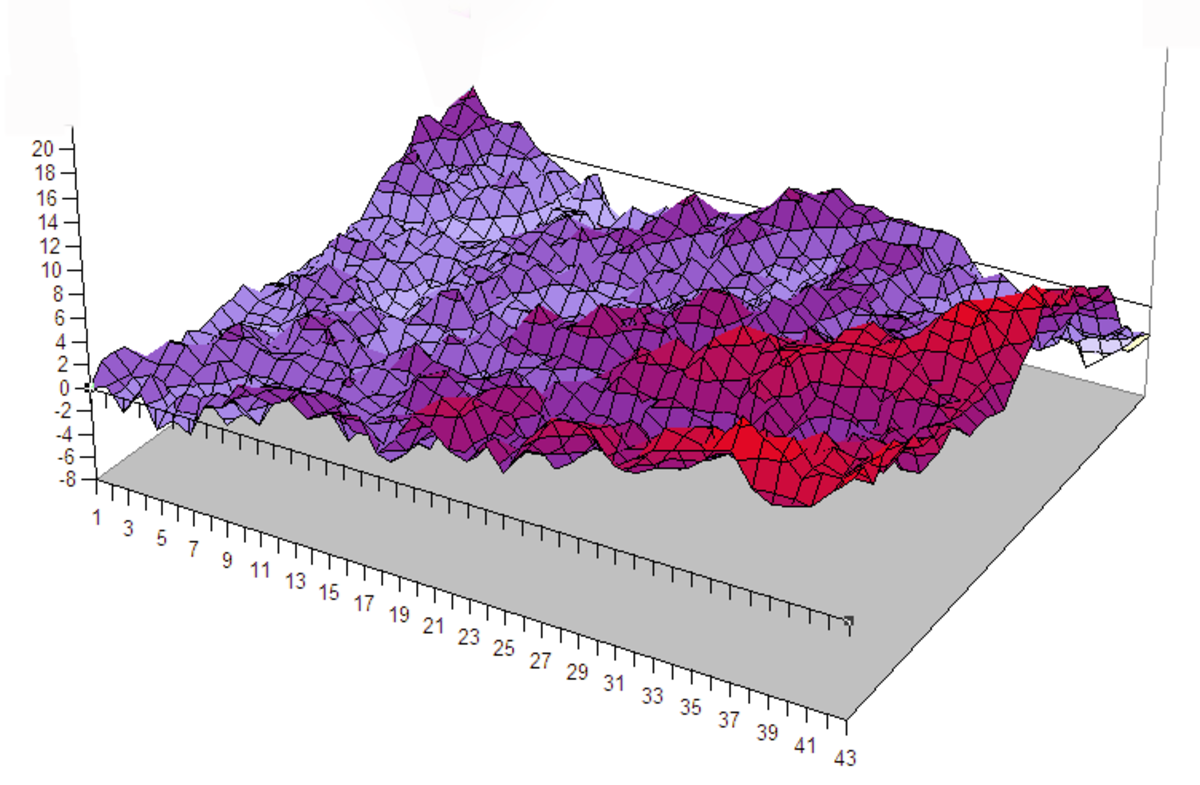
| Une fonction
|
| Mesuré | 2.52 | Amas de percolation en 3 dimensions |
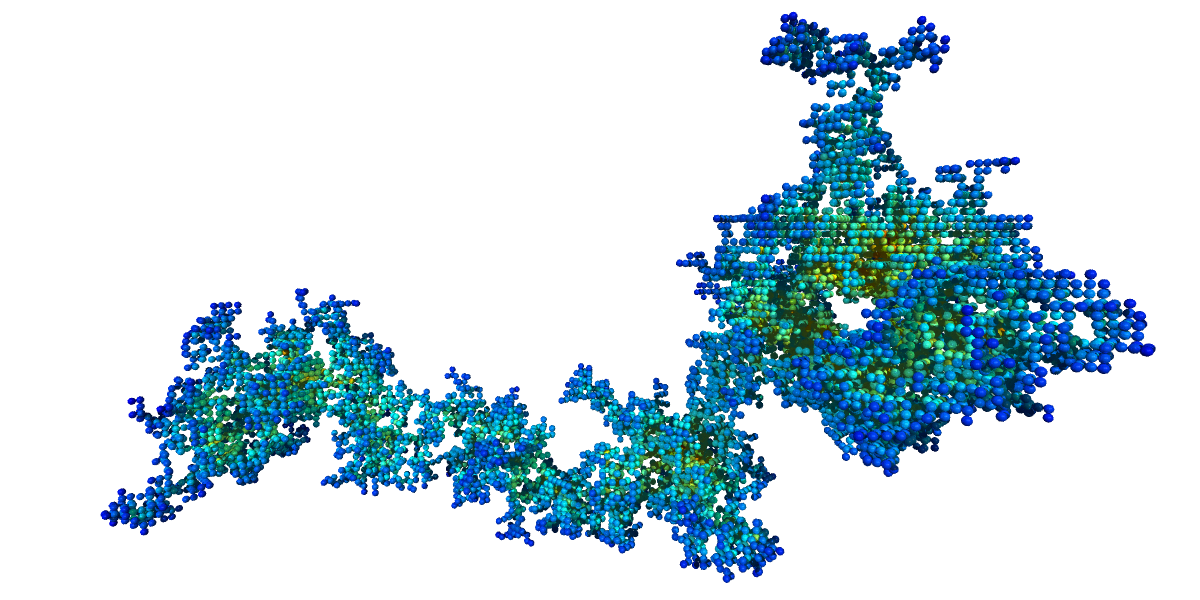
| Au seuil de percolation, l'amas 3D de percolation par invasion a une dimension fractale de 2,52 environ. |
| Mesuré | 2.66 | Brocoli |

| |
| 2.79 | Surface du cerveau humain |
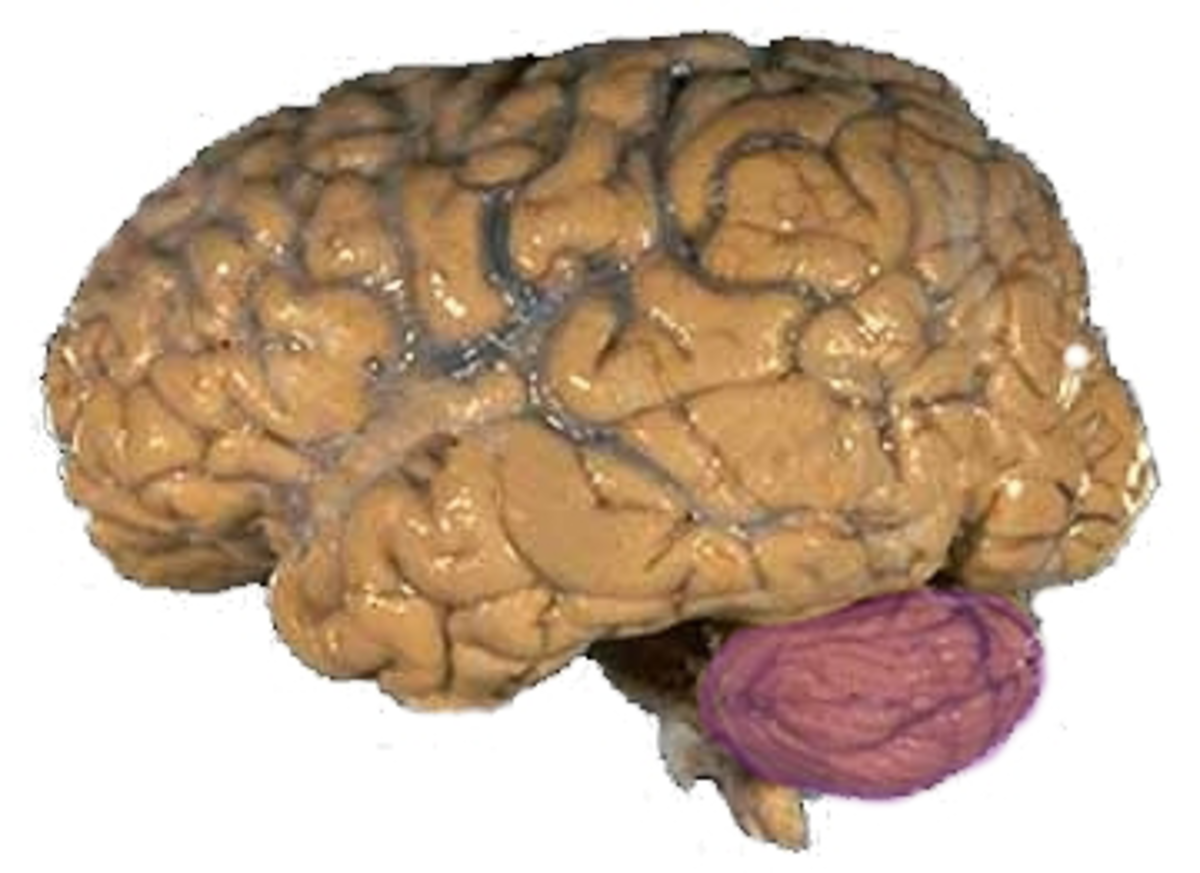
| ||
| 2,97 | Surface pulmonaire |
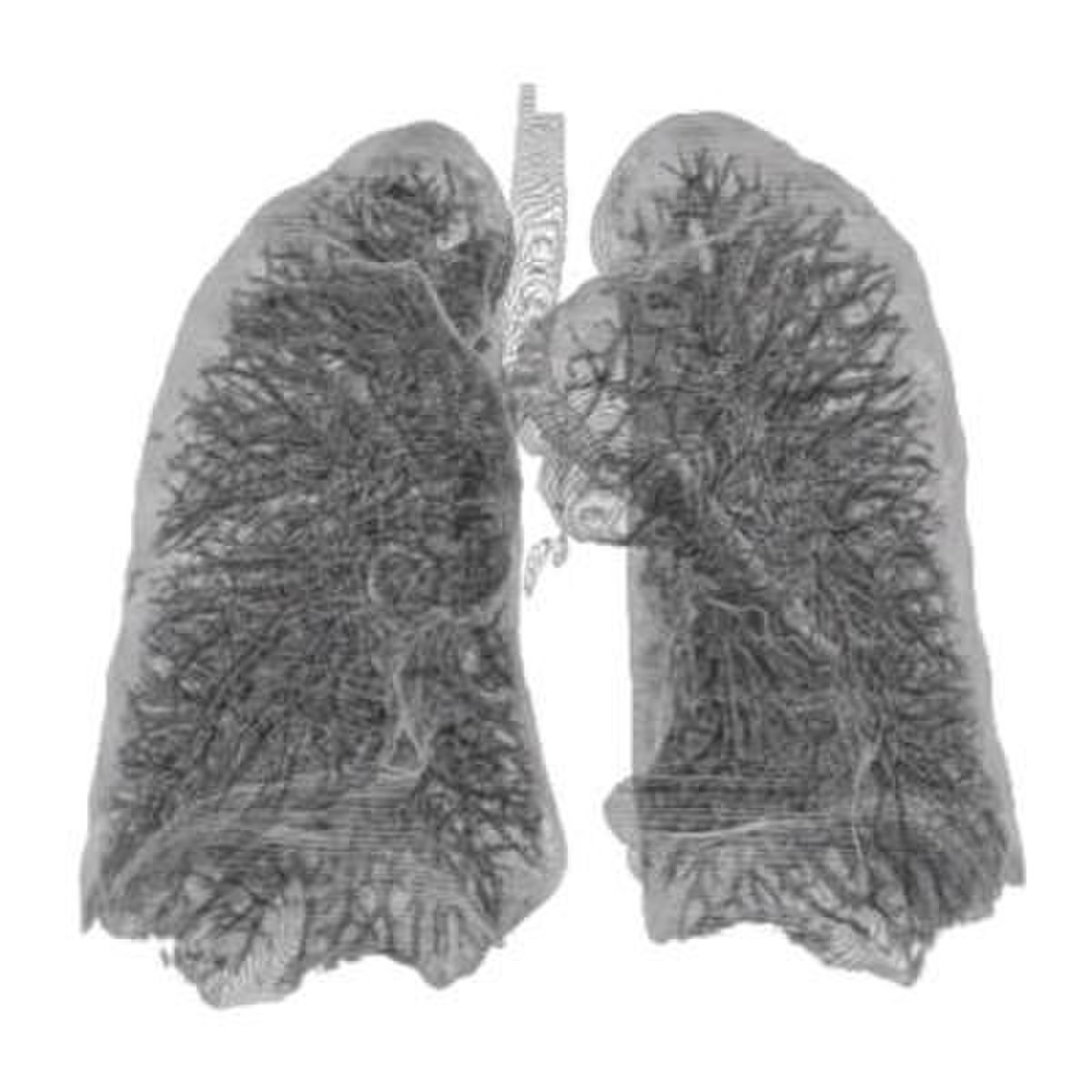
| Le réseau d'alvéoles pulmonaires forme une surface fractale proche de 3. | |
| Calculé | 3 | Corde quantique |
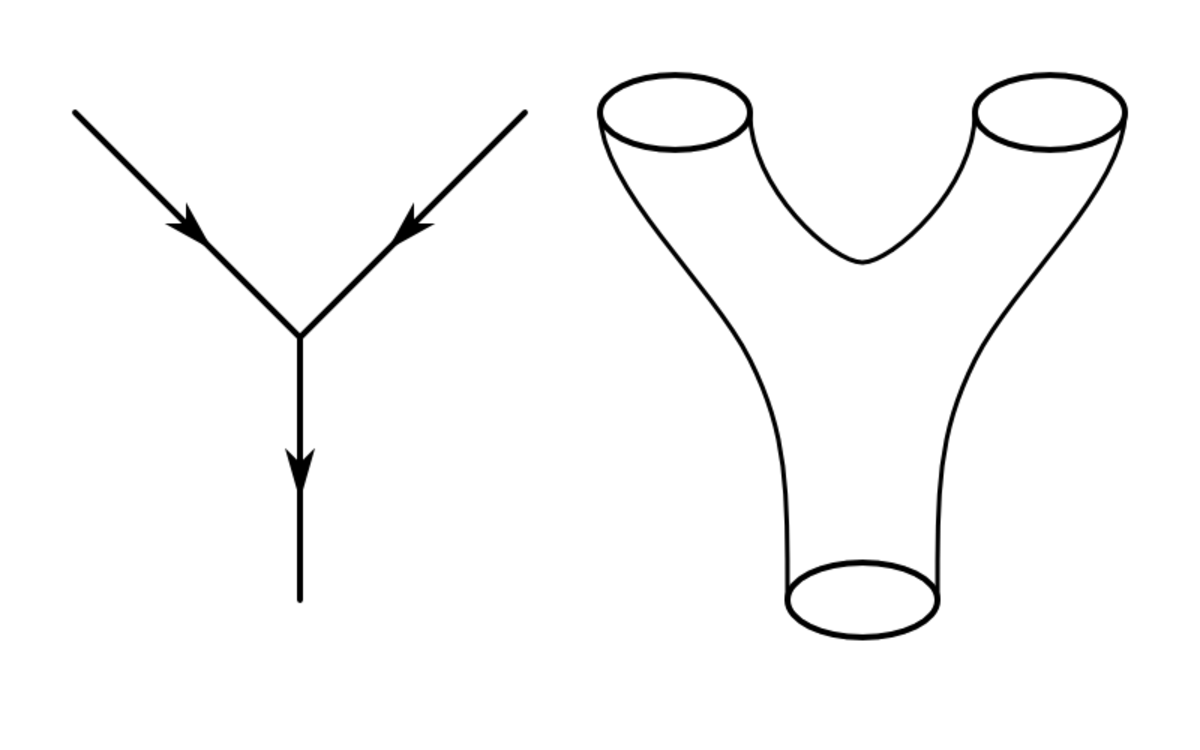
| Trajectoire d'une corde quantique dont le point représentatif dérive au hasard. |