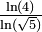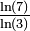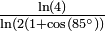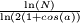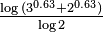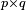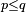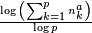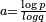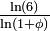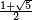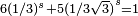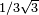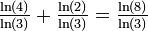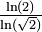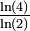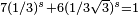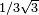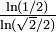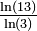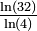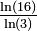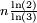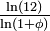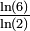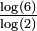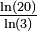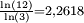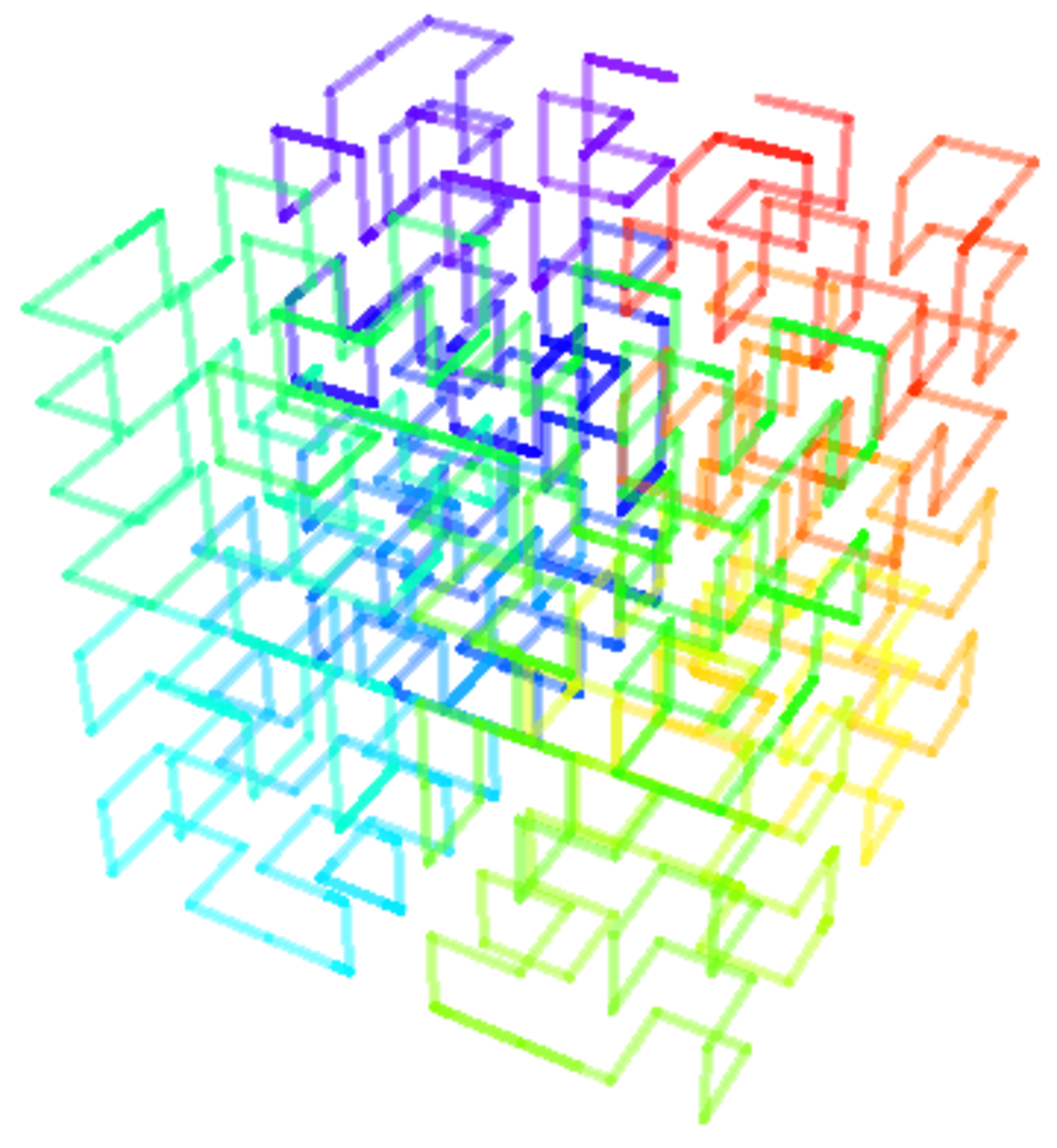Liste de fractales par dimension de Hausdorff - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
Cet article est une liste de fractales, ordonnées par dimension de Hausdorff croissante.
En mathématiques, une fractale est un ensemble dont la dimension de Hausdorff (notée δ) est strictement supérieure à la dimension topologique.
Fractales déterministes
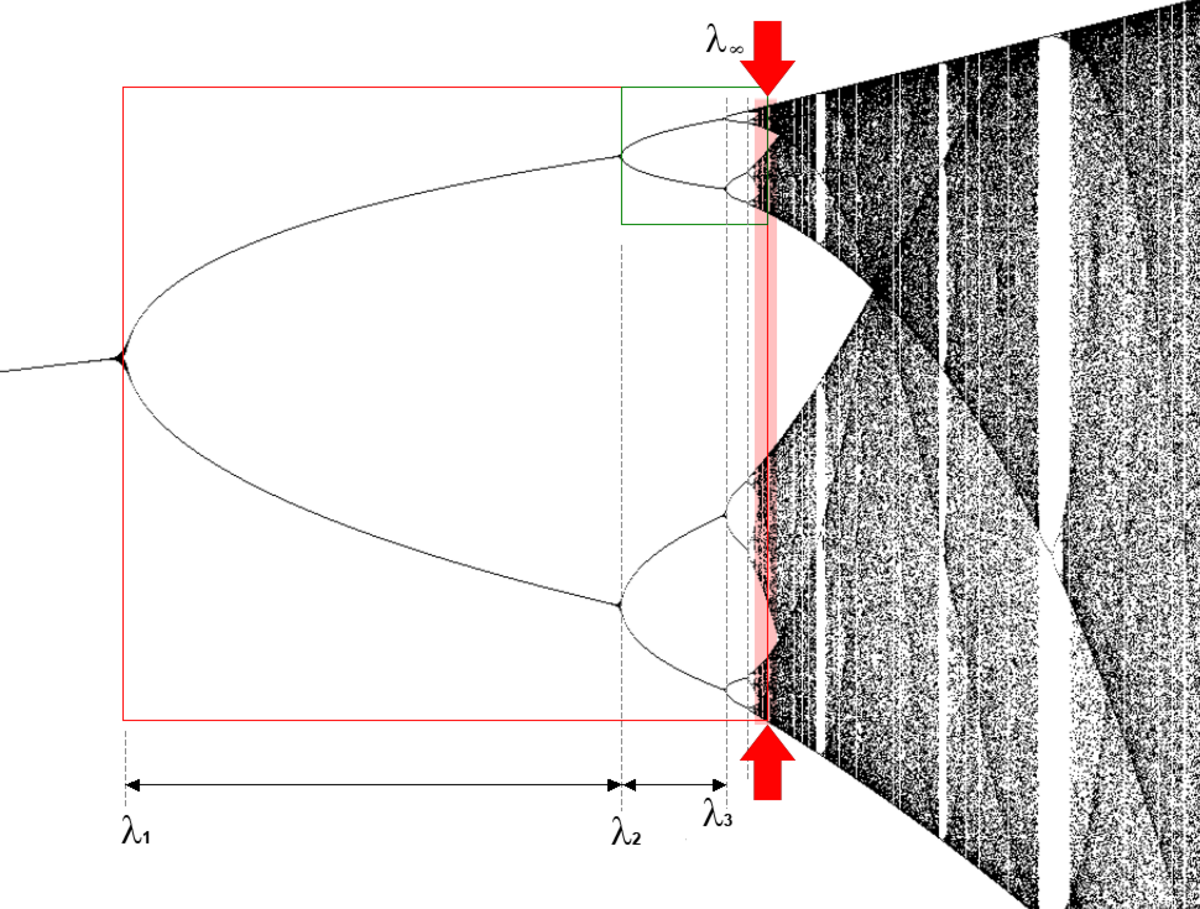
δ < 1
| δ (val. exacte) | δ (val. approchée) | Nom | Illustration | Remarques |
|---|---|---|---|---|
| 0 ⇒ donc pas une fractale mais dim box-counting = 1 | 0 | Nombres rationnels | La dimension de Hausdorff des ensembles dénombrables vaut toujours zéro. Ces ensembles ne peuvent être fractals. Ajoutons que la dimension "box counting" d'un tel ensemble peut être différent s'il s'agit d'un sous-ensemble dense d'une région ouverte de R. L'ensemble des nombres rationnels a ainsi une dimension box-counting de "1" car sa clôture est R. | |
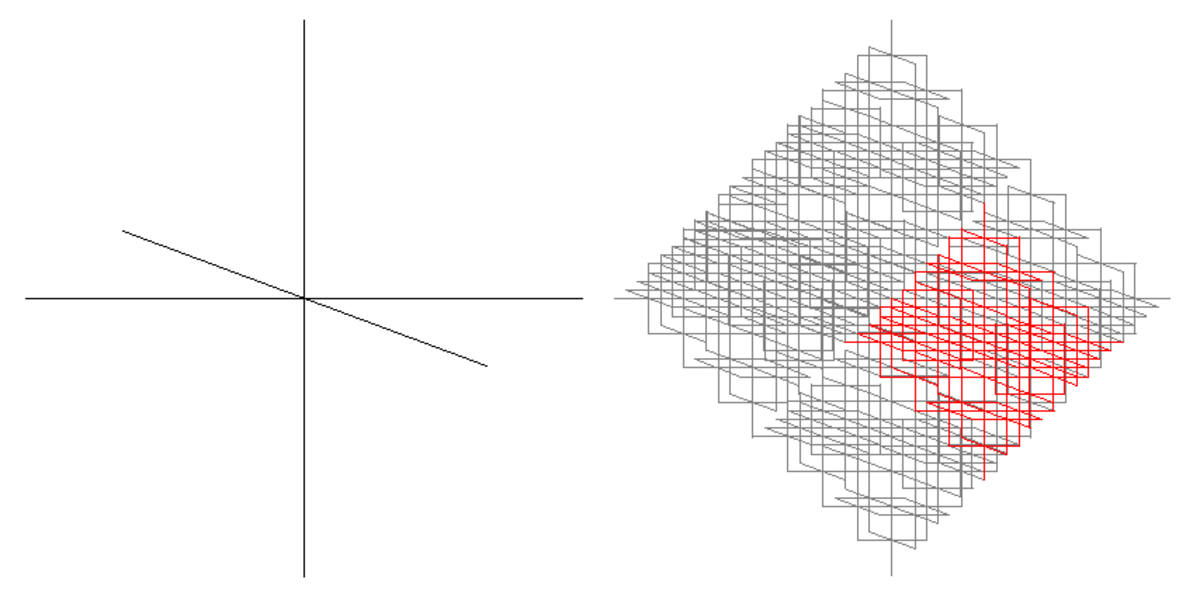
| Calculé | 0.538 | Attracteur de Feigenbaum |
| L'attracteur de Feigenbaum (entre les flèches) est l'ensemble des points générés par itérations successives de la fonction logistique pour le paramètre critique
|
|
| 0,6309 | Ensemble de Cantor | Construit en retirant le tiers central à chaque itération. Nulle part dense et de mesure nulle mais indénombrable. Généralisation : L'ensemble de Cantor généralisé se construit en retirant à chaque segment et à la neme itération, le segment central de longueur γm . Sa dimension fractale vaut alors
| |
|
| 0.6942 | Ensemble de Cantor asymétrique |

| Remarquer que la dimension n'est plus
|
|
| 0.69897 | Nombres réels avec décimales paires |
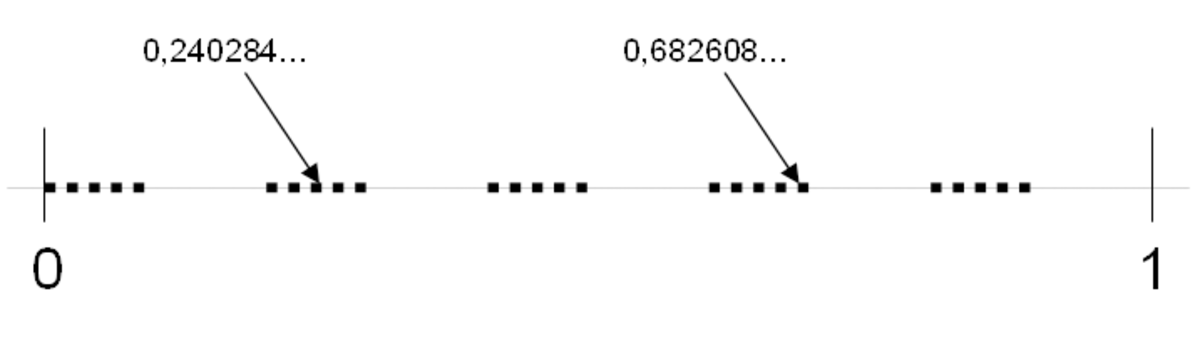
| Similaire à un ensemble de Cantor. |
|
| 0,7325 | Fractale UNU | Fractale auto-descriptive construite par itérations successives du schéma suivant : u → unu (un « u ») → unuunnunu (un « u », un « n », un « u ») → etc. |
1 ≤ δ < 2
| δ (val. exacte) | δ (val. approchée) | Nom | Illustration | Remarques |
|---|---|---|---|---|
| 1 | 1.0000 | Ensemble de Smith-Volterra-Cantor |

| Construit en retirant le quart, puis le seizième, le 64e… central à chaque itération. N'est nulle part dense mais est indénombrable et a pour mesure de Lebesgue 1/2. Il a donc pour dimension 1. |
|
| 1.0000 | Courbe de Takagi ou Blancmange |
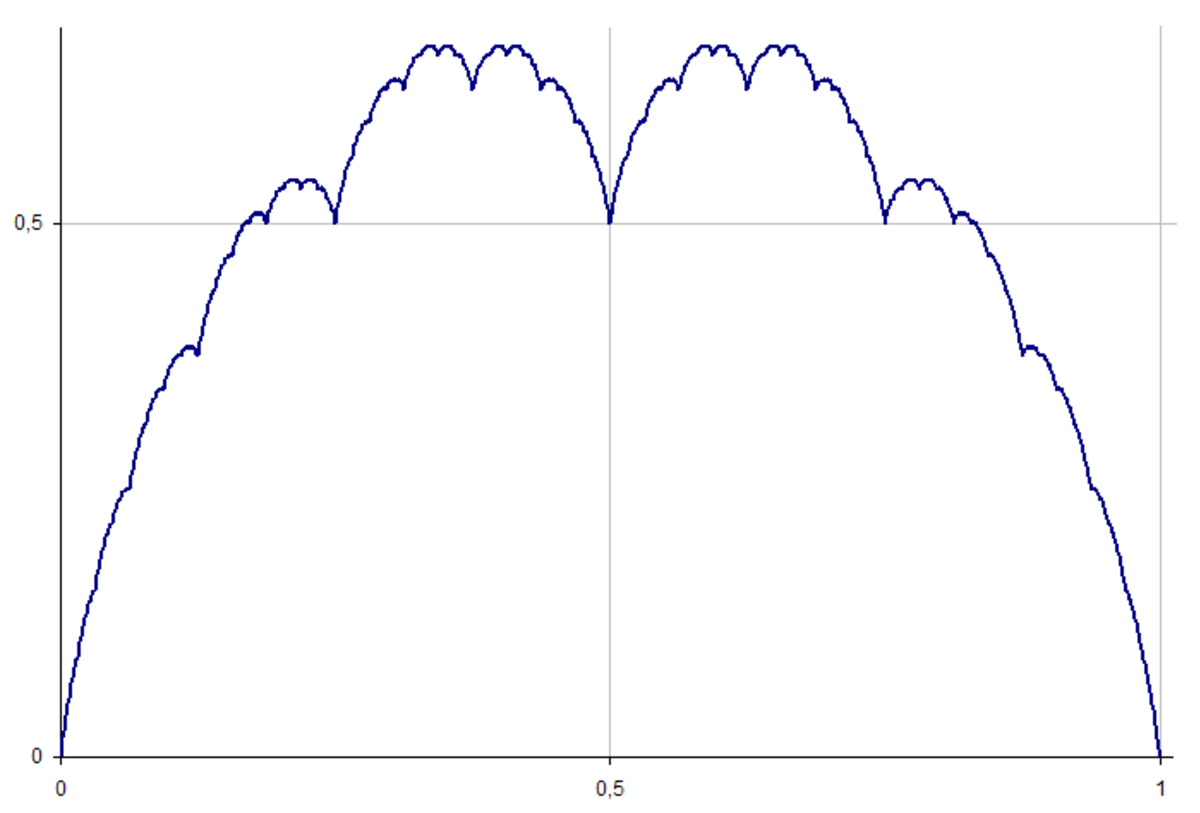
| Définie sur l'intervalle unité par
|
| calculé | 1.0812 | Ensemble de Julia z² + 1/4 |

| Ensemble de Julia pour c = 1/4. |
| Solution s de 2 | α | 3s + | α | 4s = 1 | 1.0933 | Frontière de la Fractale de Rauzy |

| Représentation géométrique du système dynamique associé à la substitution de Tribonacci:
|
| 1,12915 | Île de Gosper |

| Baptisée par Mandelbrot (1977). Frontière de la courbe de Gosper. | |
| Mesuré (Box counting) | 1.2 | Ensemble de Julia "Dendrite" |
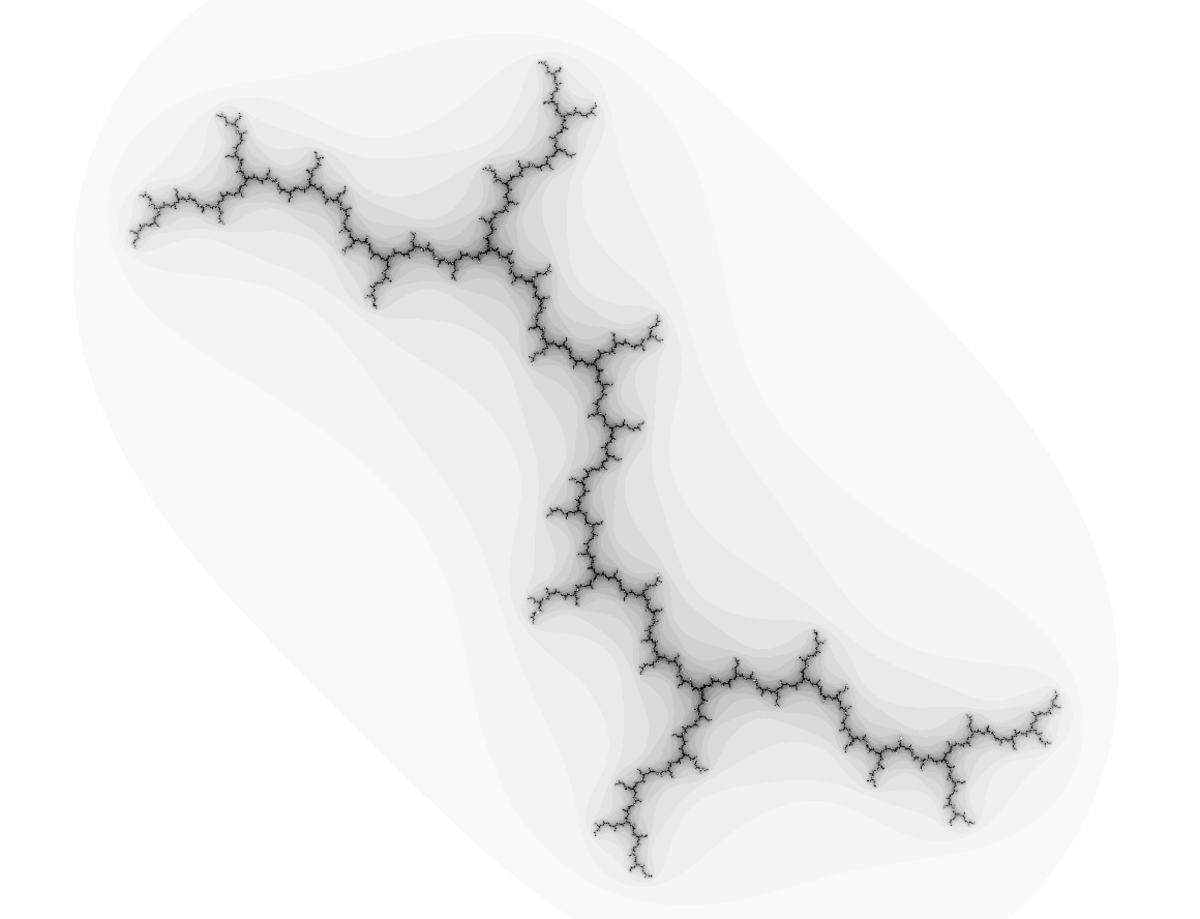
| Ensemble de Julia pour c=i |
|
| 1.2083 | Fractale du mot de Fibonacci à 60 ° |

| Construite à partir du Mot de Fibonacci, avec un angle à 60°. Voir aussi la fractale du mot de Fibonacci standard, ci-dessous. Avec
|
| 1.2107 | Frontière du tame twindragon |

| Un des six 2-autopavés réguliers (peut être pavé par deux copies de lui-même, de même taille). | |
|
| 1.2465 | Frontière de la fractale du mot de Fibonacci |
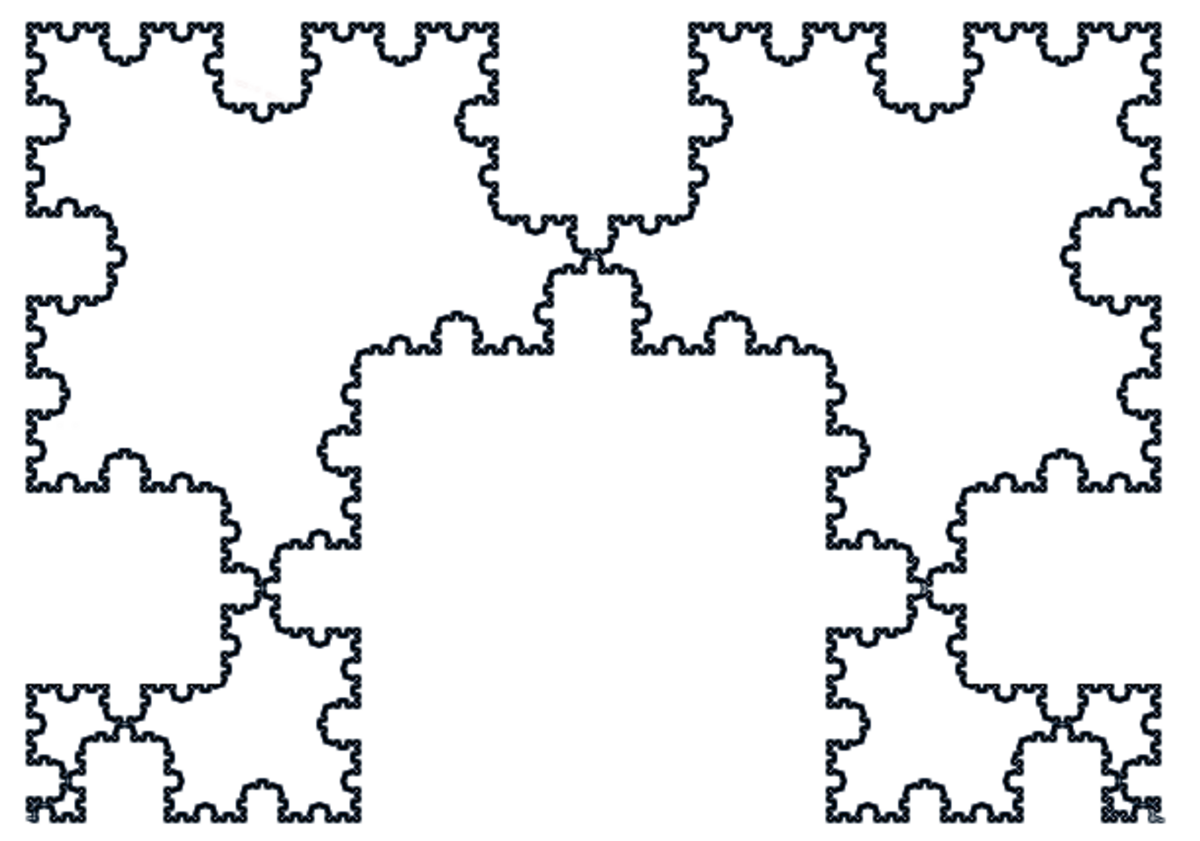
| Construite à partir du Mot de Fibonacci. Voir aussi la fractale du mot de Fibonacci standard, ci-dessous. Avec
|
| 1,26 | Attracteur de Hénon |

| La carte de Hénon canonique (a = 1,4 et b = 0.3) possède δ = 1,261 ± 0,003. Différents paramètres conduisent à différentes valeurs de δ | |
| 1,2619 | Courbe de Koch |
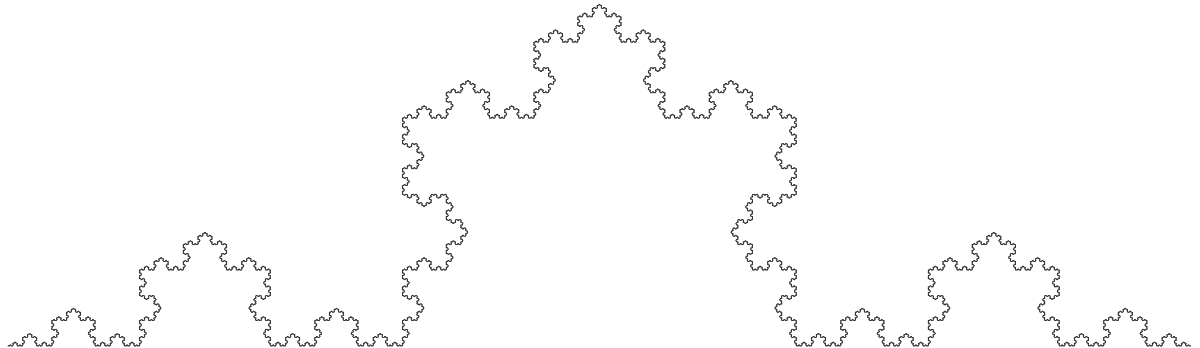
| En juxtaposant 3 fois cette courbe en triangle on obtient le flocon de Koch et l'anti-flocon de Koch si elle est inversée. | |
| 1,2619 | Frontière de la Courbe Terdragon, Fudgeflake |

| L-System : similaire à la courbe du dragon avec un angle de 30°. Le Fudgeflake est construit en juxtaposant 3 segments initiaux en triangle. | |
| 1,2619 | Carré de Cantor | Ensemble de Cantor en deux dimensions. | ||
| calculé | 1,2683 | Ensemble de Julia pour z²-1 |
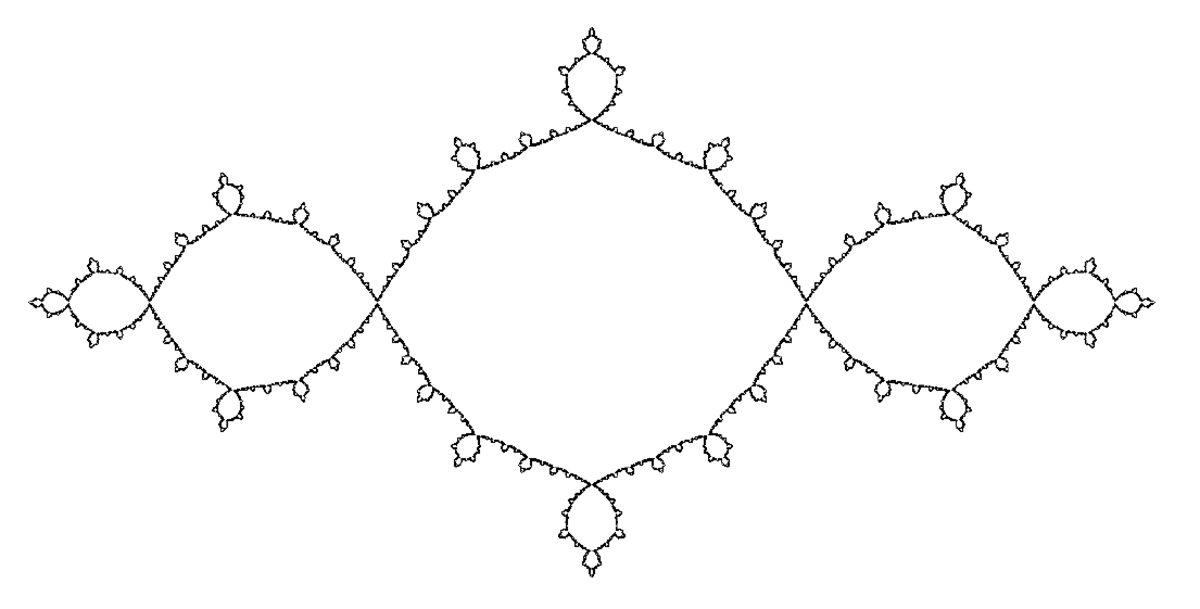
| Ensemble de Julia pour c=-1. |
| Mesuré (box-counting) | 1,3 | Fractale Beryl pour k=1 |

| Pour k=1. La fractale Béryl est définie par f(x, y)→(k(x+y), xy) avec x et y complexes et la coupe dans le plan ν0 = 1 |
| calculé | 1,3057 | Baderne d'Apollonius |
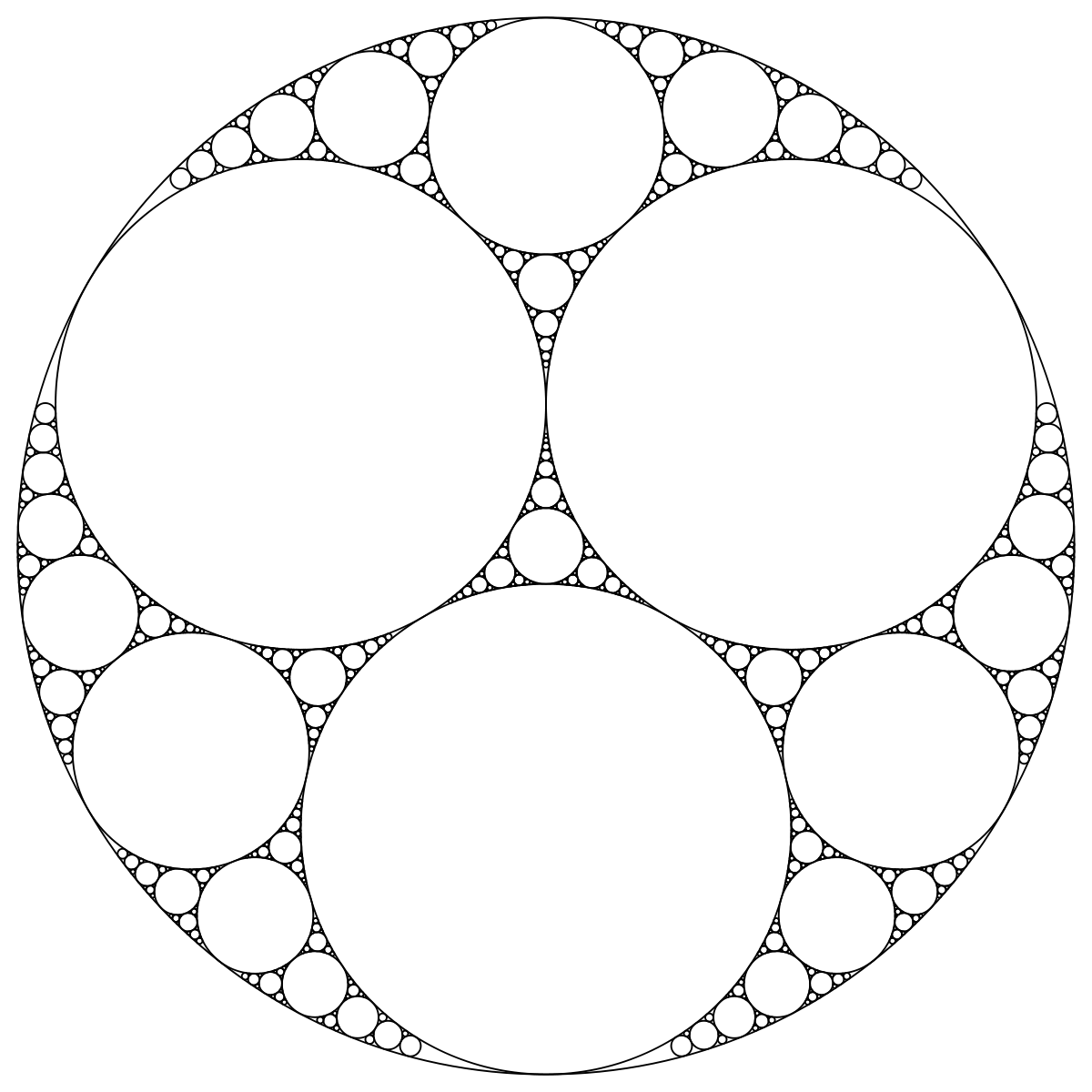
| Voir |
| calculé (box-counting) | 1.328 | Fractale d'inversion à 5 cercles |
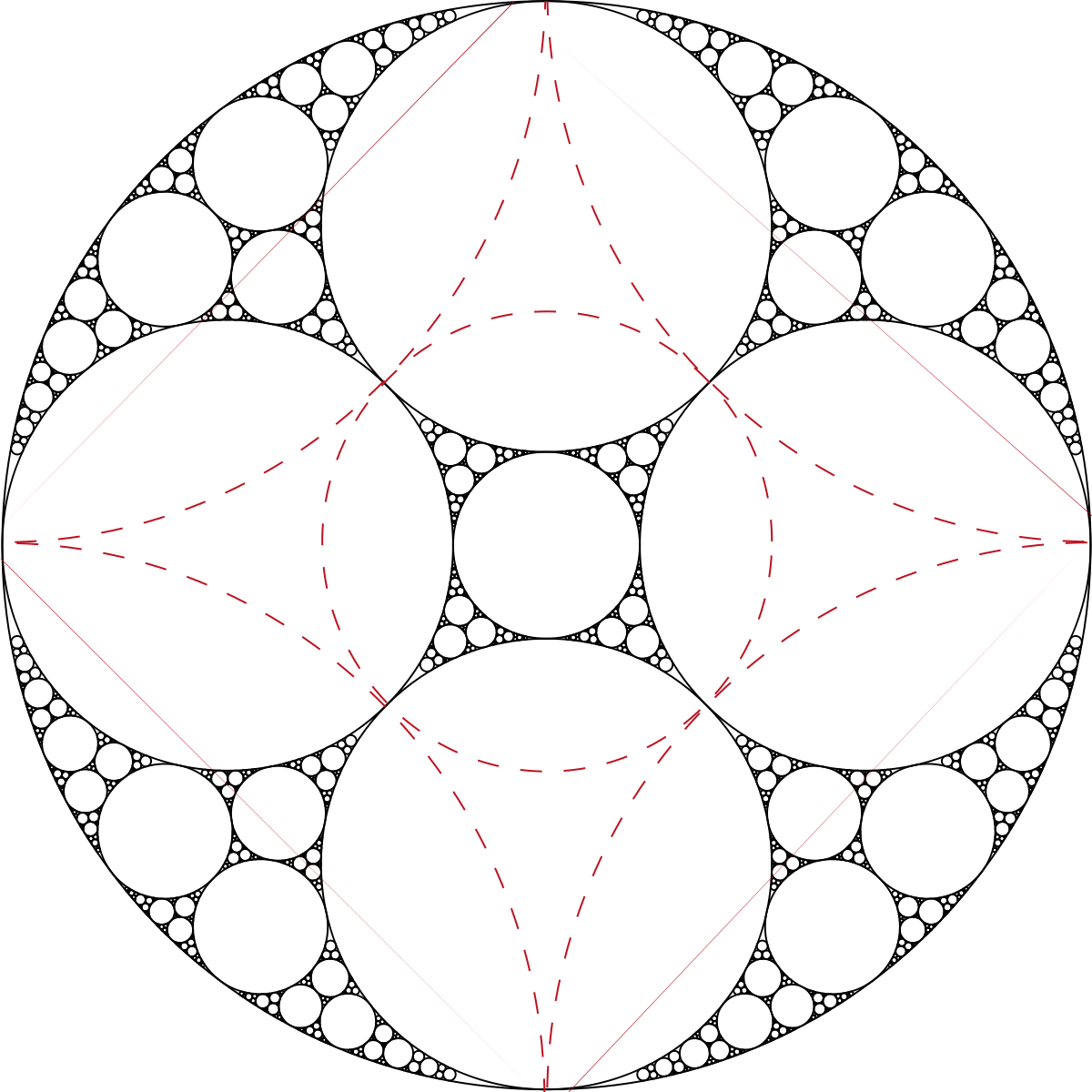
| L'ensemble limite généré itérativement via des inversions par rapport à 5 cercles tangents. Également une baderne d'Apollonius à 4 cercles de base. Voir |
| calculé | 1.3934 | Lapin de Douady |
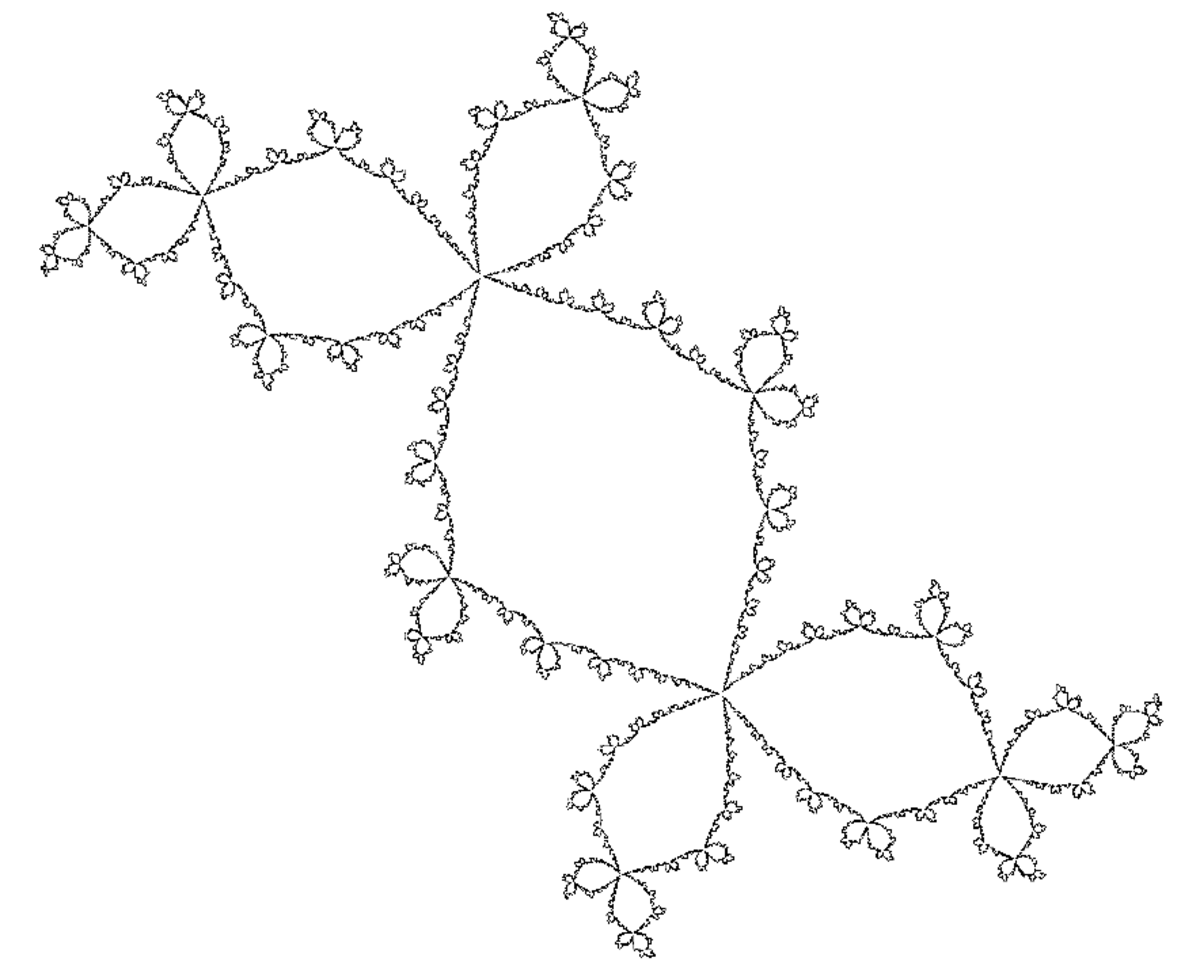
| Ensemble de Julia pour c=-0,123+0.745i. |
| Mesuré (box counting) | 1,42 +/- 0,02 | Fractale de Newton |
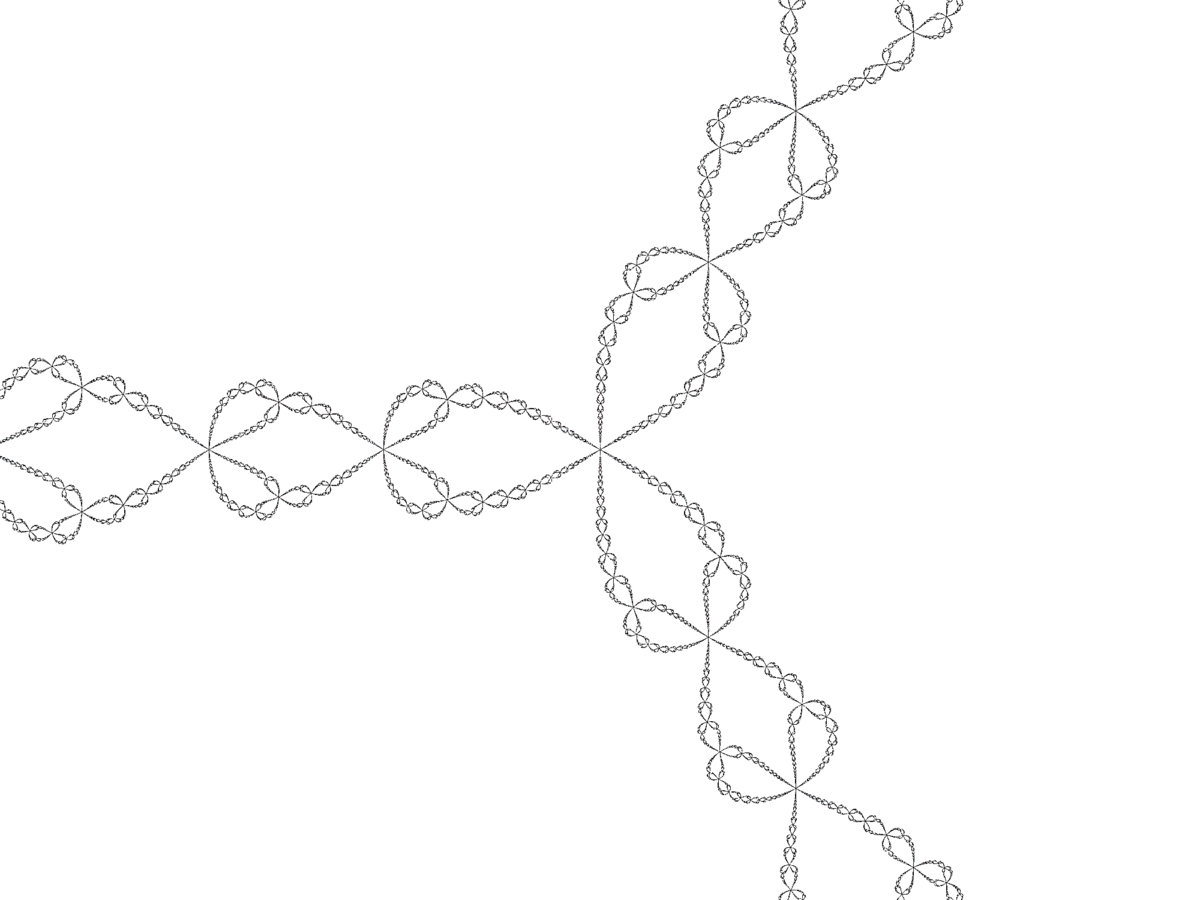
| Frontière triple des bassins d'attraction des 3 racines complexes de l'equation z3 − 1 = 0 par la méthode de Newton. |
|
| 1,4649 | Fractale de Vicsek |

| Construit en substituant itérativement chaque carré par une croix de 5 carrés. |
|
| 1,4649 | Courbe de Koch quadratique (type 1) |

| On y retrouve le motif de la fractale box (voir ci-dessus), construit différemment. |
|
| 1,5000 | Courbe de Koch quadratique (type 2) |

| Appelée également « saucisse de Minkowski ». |
|
| 1.5000 | une fonction de Weierstrass:
|
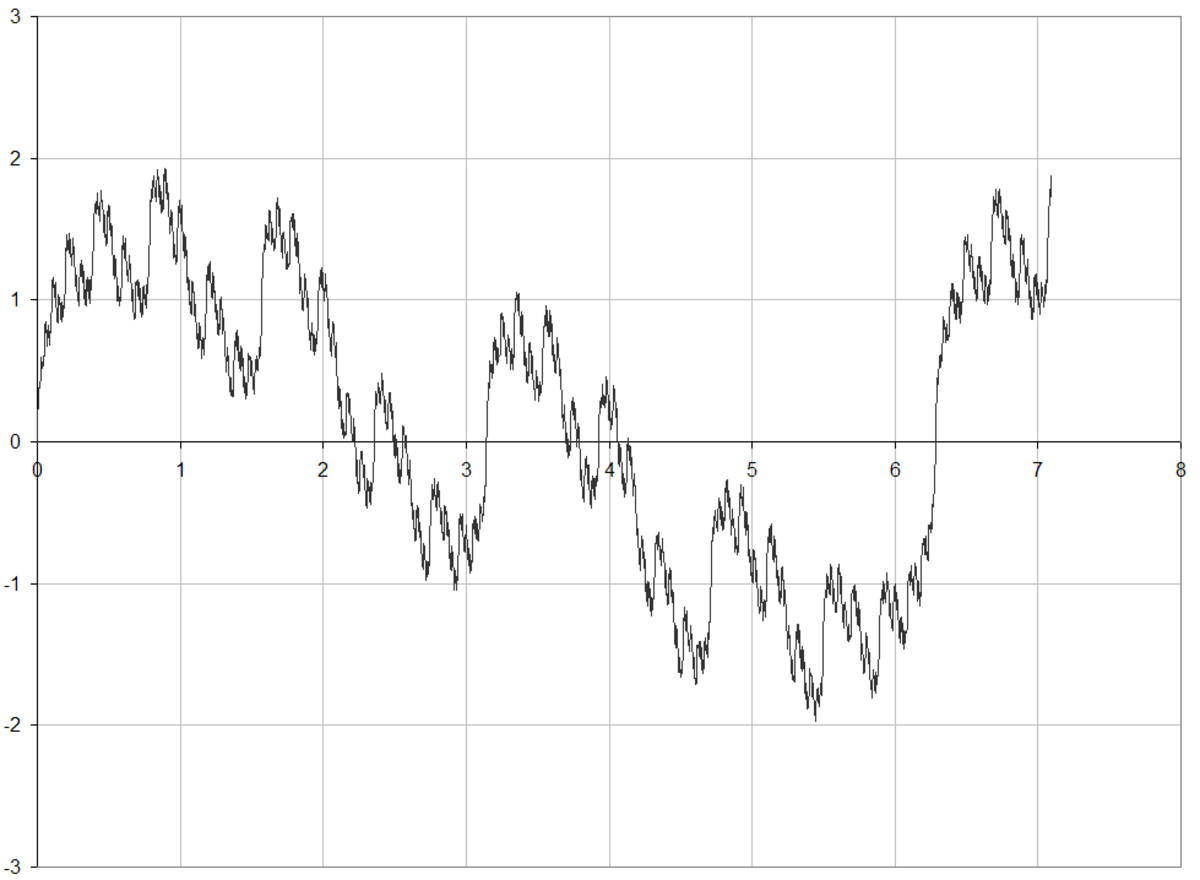
| La dimension de Hausdorff de la fonction de Weierstrass
|
|
| 1,5236 | Frontière courbe du dragon |

| Cf. Chang & Zhang. |
|
| 1.5236 | Frontière du twindragon |

| Un des six 2-autopavés réguliers (peut être pavé par deux copies de lui-même, de même taille). |
|
| 1,5850 | Arbre à trois branches |
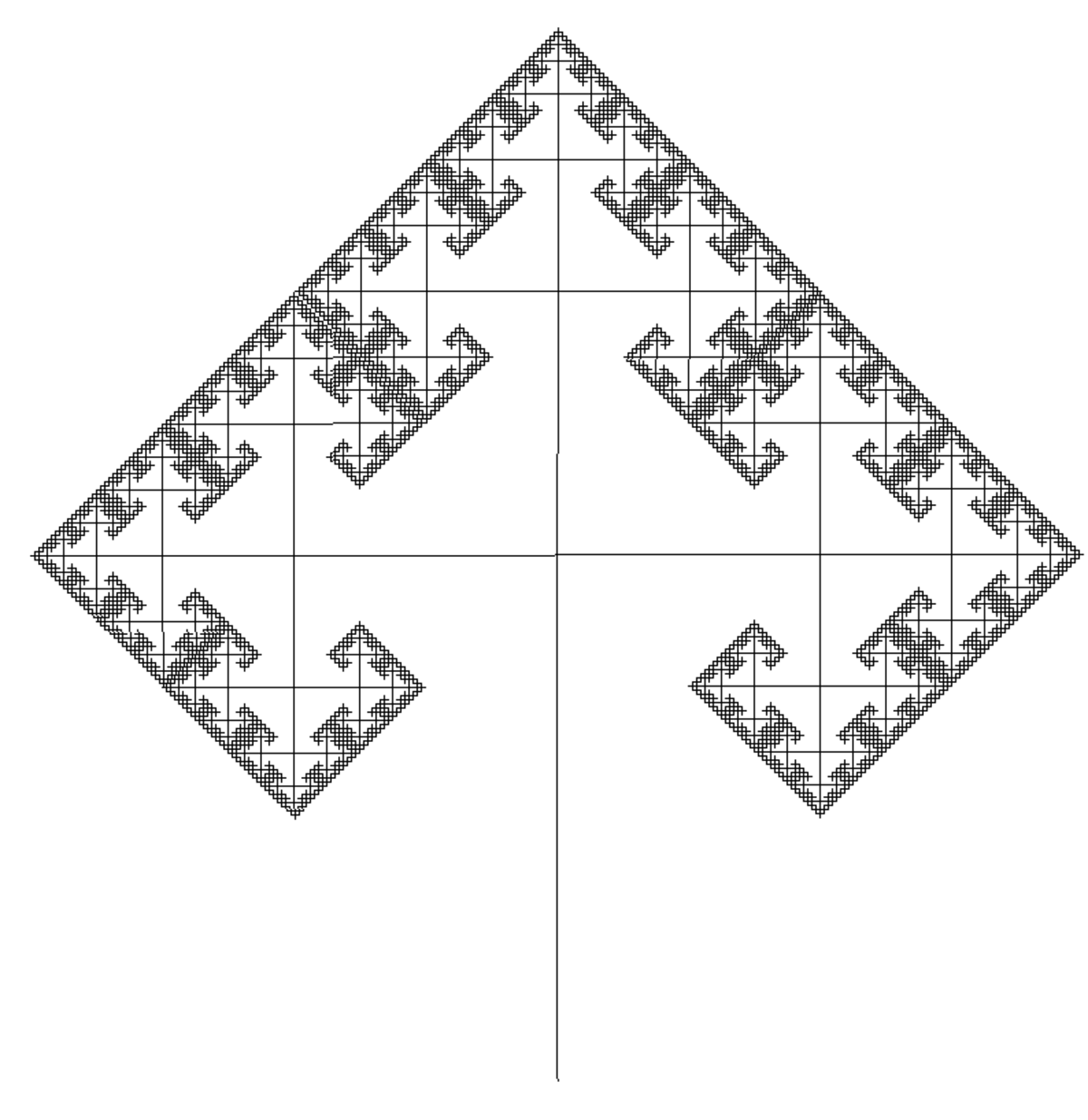
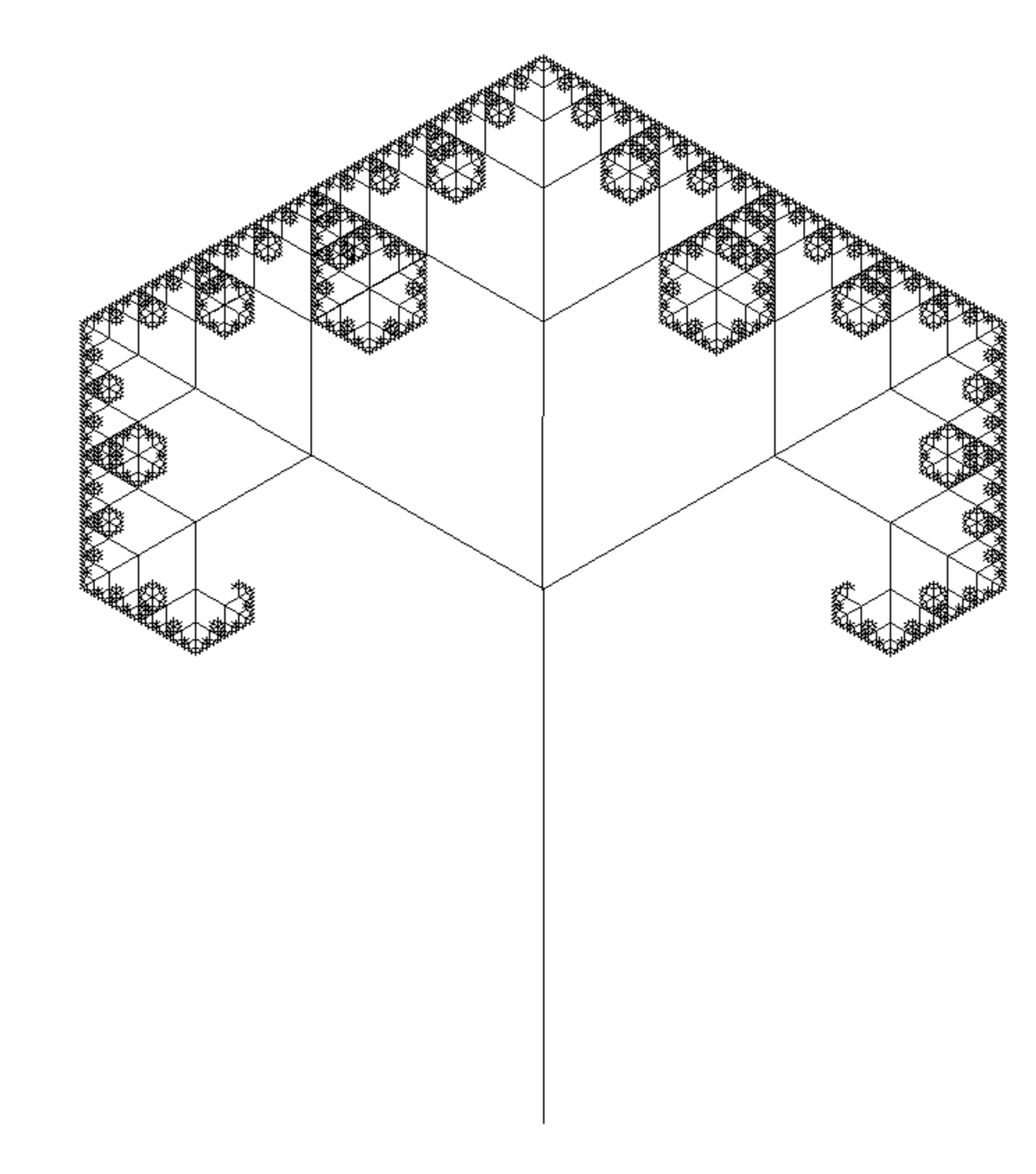
| Chaque branche porte trois branches (ici 90 ° et 60°). La dimension fractale de l'arbre est celle des branches terminales. |
|
| 1,5850 | Triangle de Sierpiński |

| C'est également le triangle de Pascal modulo 2. |
|
| 1,5850 | Courbe de Sierpiński en pointe de flèche |
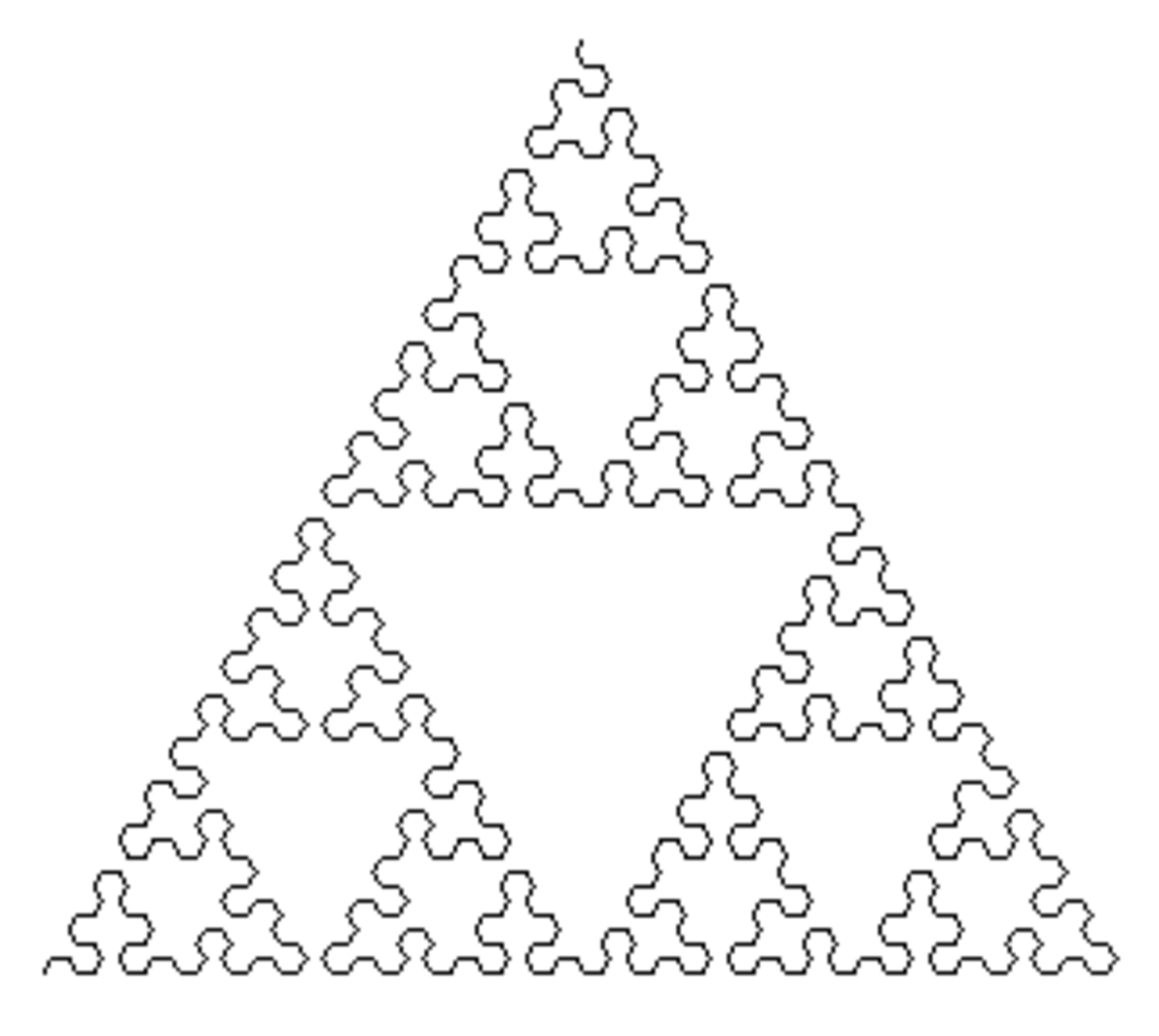
| Même limite que le triangle de Sierpiński (ci-dessus), mais obtenue par itérations d'une courbe unidimensionnelle. |
|
| 1,61803 =
| un dragon d'or |
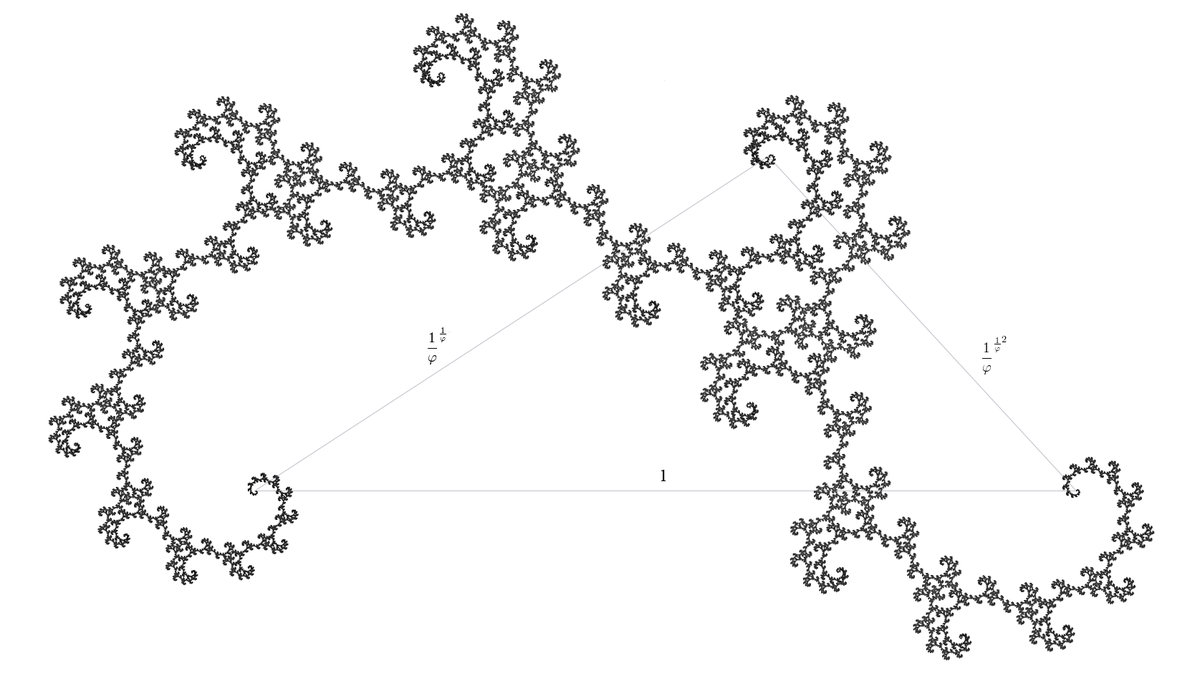
| Construit avec deux homothéties de rapport r et r2, avec
|
| 1 + log3(2) | 1,6309 | Triangle de Pascal modulo 3 |

| D'une manière générale pour un triangle modulo k, si k est premier, la dimension fractale est
|
|
| 1,6379 | Fractale du mot de Fibonacci |

| Fractale basée sur le mot de Fibonacci (ou séquence du Lapin) Sloane A005614. Illustration : Fractale après F23 = 28657 segments.. Avec
|
| Solution de
| 1.6402 | Attracteur d'un IFS avec 3 similitudes de ratios 1/3, 1/2 and 2/3 |
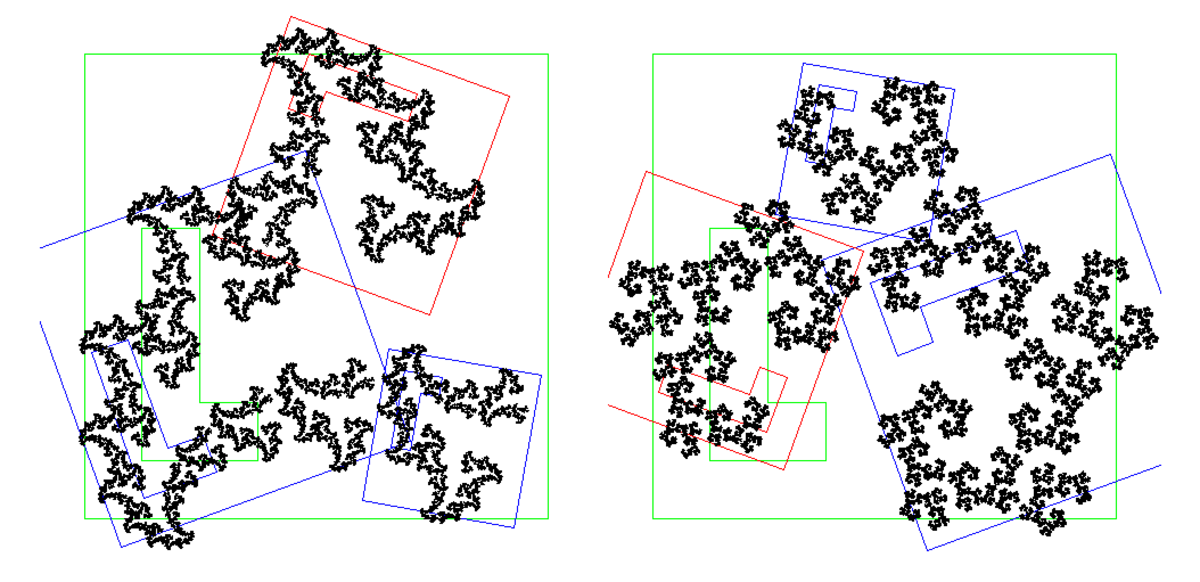
| Generalisation : Supposant la condition d'ensemble ouvert satisfaite, l'attracteur d'un système de fonctions itérées à n simulitudes de ratio cn, a pour dimension de Hausdorff s, solution de l'équation :
|
| 1 + log5(3) | 1,6826 | Triangle de Pascal modulo 5 |

| D'une manière générale pour un triangle modulo k, si k est premier, la dimension fractale est
|
| Mesuré (box-counting) | 1.7 | Attracteur d'Ikeda |

| Pour les valeurs de paramètres a=1, b=0.9, k=0.4 et p=6 dans le système itéré d'Ikeda
|
|
| 1,7227 | Fractale Pinwheel |
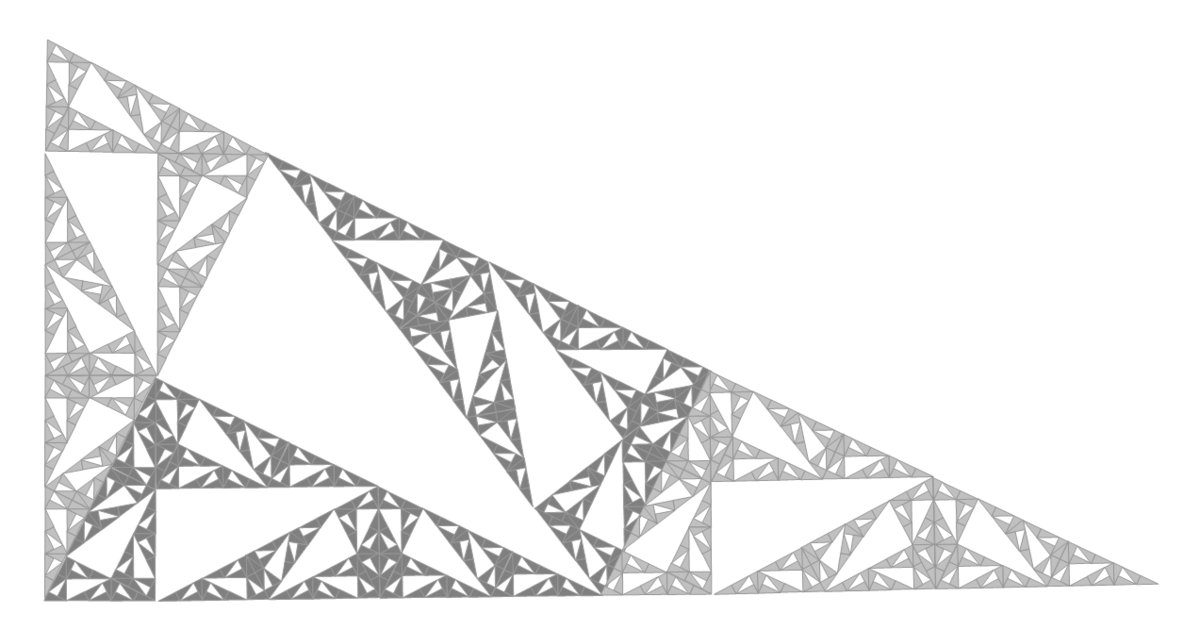
| Construite à partir du pavage "pinwheel" de John Conway. |
|
| 1,7712 | Flocon hexagonal |  | Construit en substituant itérativement chaque hexagone par un flocon de 7 hexagones. Sa frontière est le flocon de Koch. Contient une infinité de flocons de Koch (en positif comme en négatif). |
|
| 1,7848 | Courbe de Koch à 85 °, fractale de Cesàro |

| Généralisation de la courbe de Koch basée sur un angle a choisi entre 0 et 90°. La dimension fractale vaut alors
|
|
| 1.8272 | Une fractale auto-affine |

| Construite itérativement à partir d'une grille
|
|
| 1,8617 | Flocon pentagonal (pentaflake) |
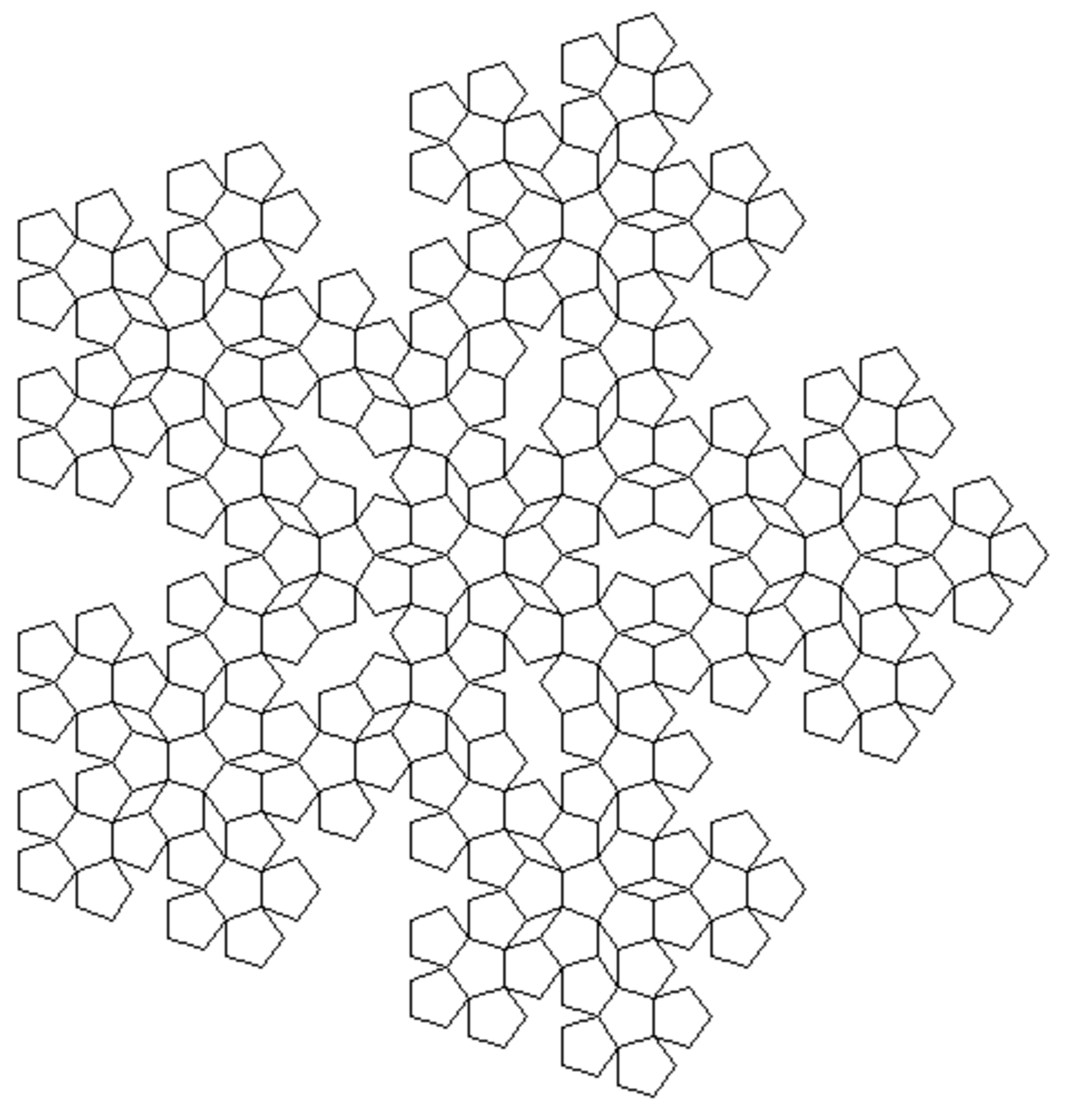
| Construit en substituant itérativement chaque pentagone par un flocon de 6 pentagones. Ici, φ est le nombre d'or et vaut
|
| solution de
| 1.8687 | L'"arbre des singes" |
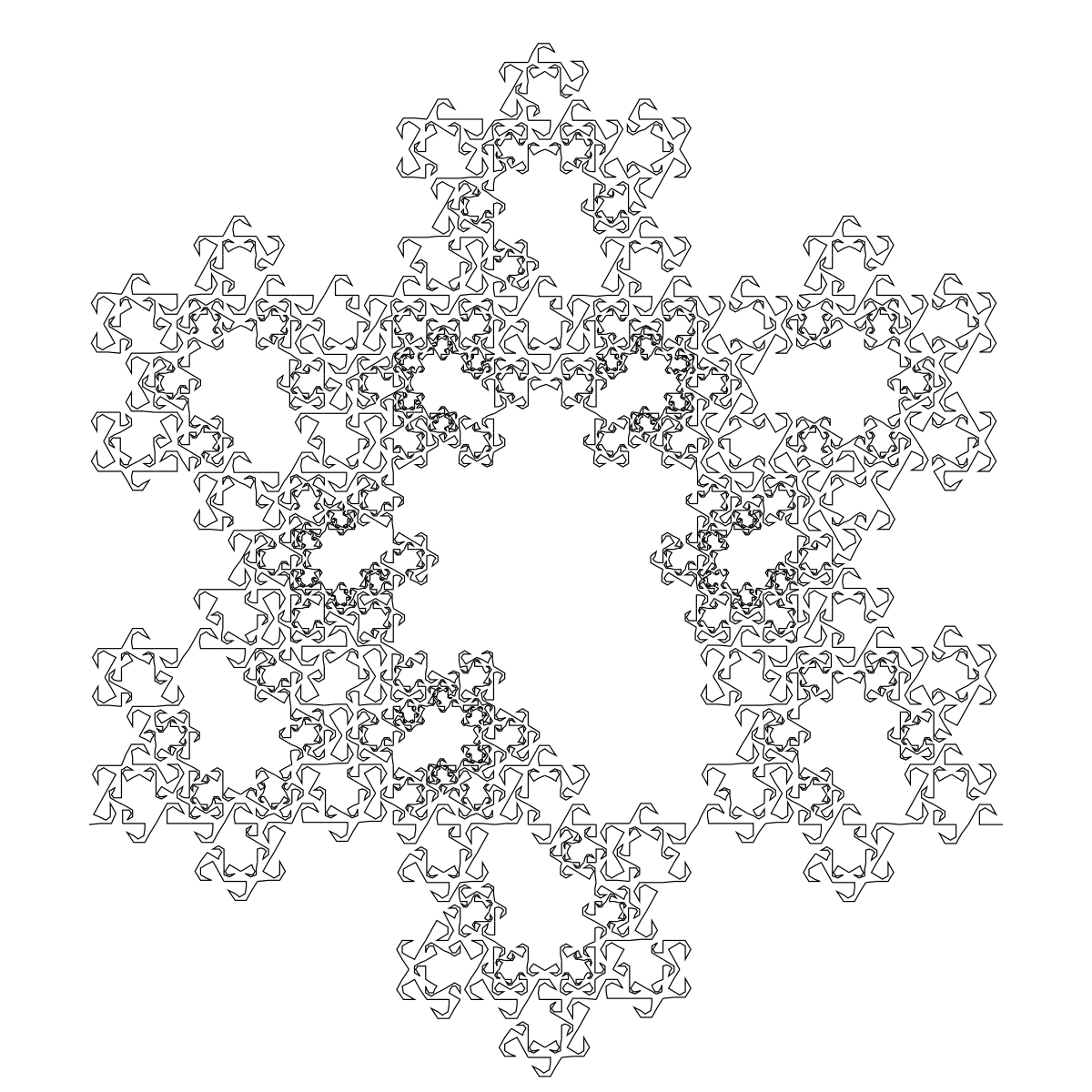
| Cette courbe apparaît sous ce nom dans "Fractal geometry of Nature" (1983) de Benoit Mandelbrot. Elle est basée sur 6 homothéties de rapport 1 / 3 et 5 homothéties de rapport
|
| 1,8928 | Tapis de Sierpiński |

| ||
| 1,8928 | Cube de Cantor |

| Ensemble de Cantor en trois dimensions. | |
|
| 1,8928 | Produit cartésien de la Courbe de von Koch et de l'ensemble de Cantor |

| Généralisation : Soit FxG, le produit cartésien de deux ensembles fractals F et G. Alors DimH(FxG) = DimH(F) + DimH(G). |
| Estimé | 1,9340 | Frontière de la fractale de Lévy |
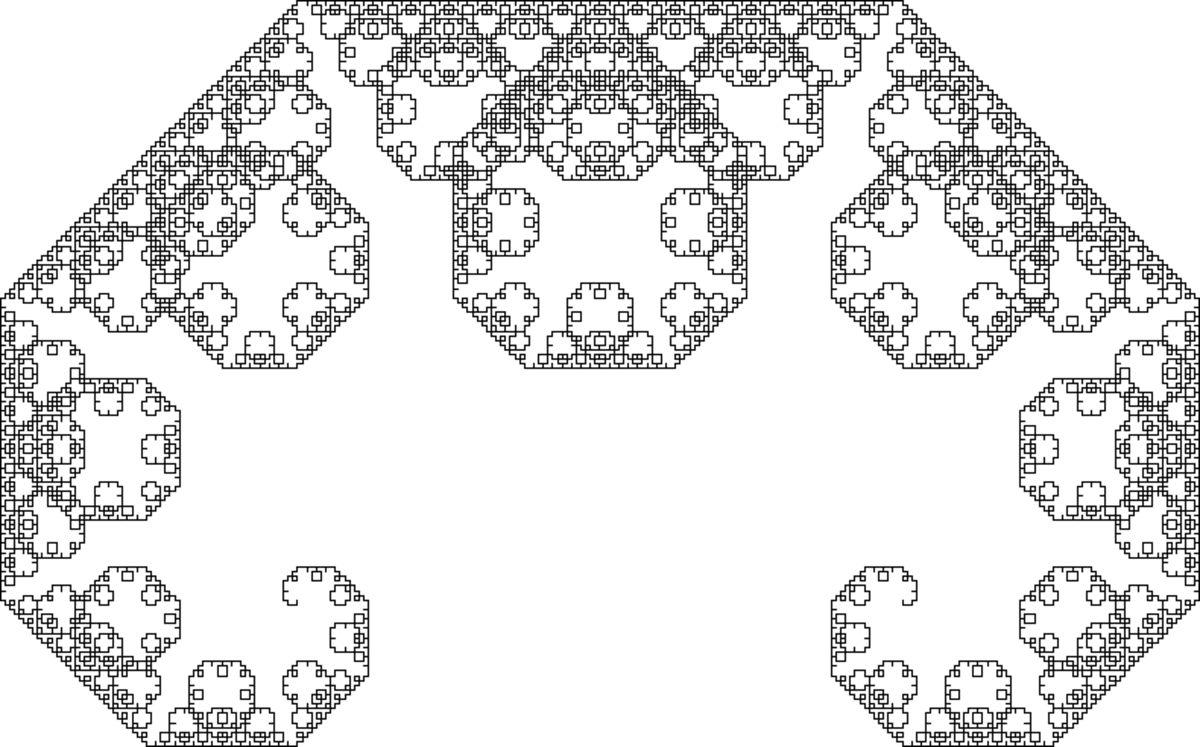
| Estimé par Duvall et Keesling (1999). La fractale de Lévy en elle-même a pour dimension de Hausdorff 2. |
| 1,974 | Pavage de Penrose | 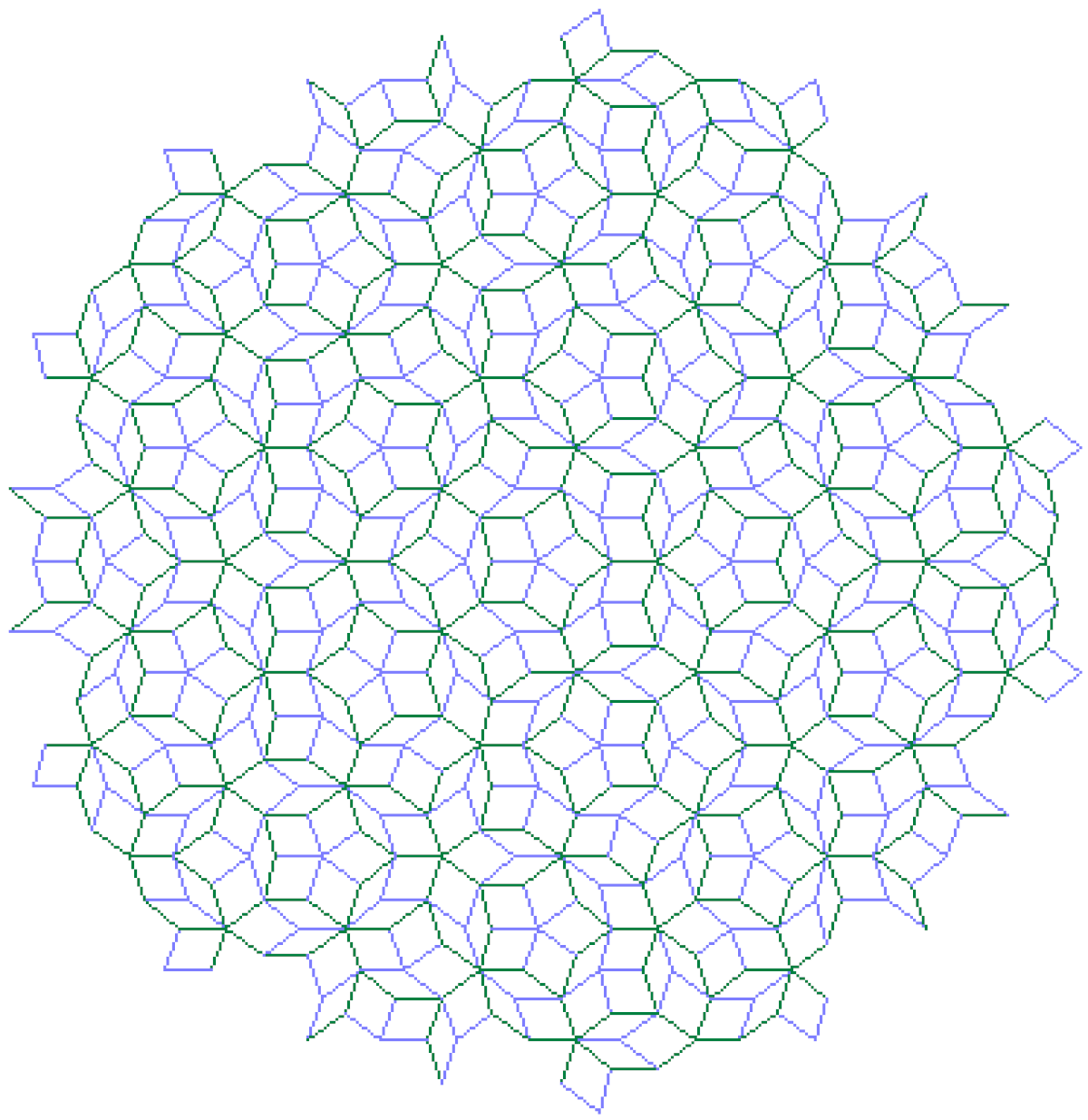 | Cf. Ramachandrarao, Sinha & Sanyal |
δ = 2
| δ (val. exacte) | δ (val. approchée) | Nom | Illustration | Remarques |
|---|---|---|---|---|
| 2 | 2 | Frontière de l'ensemble de Mandelbrot |
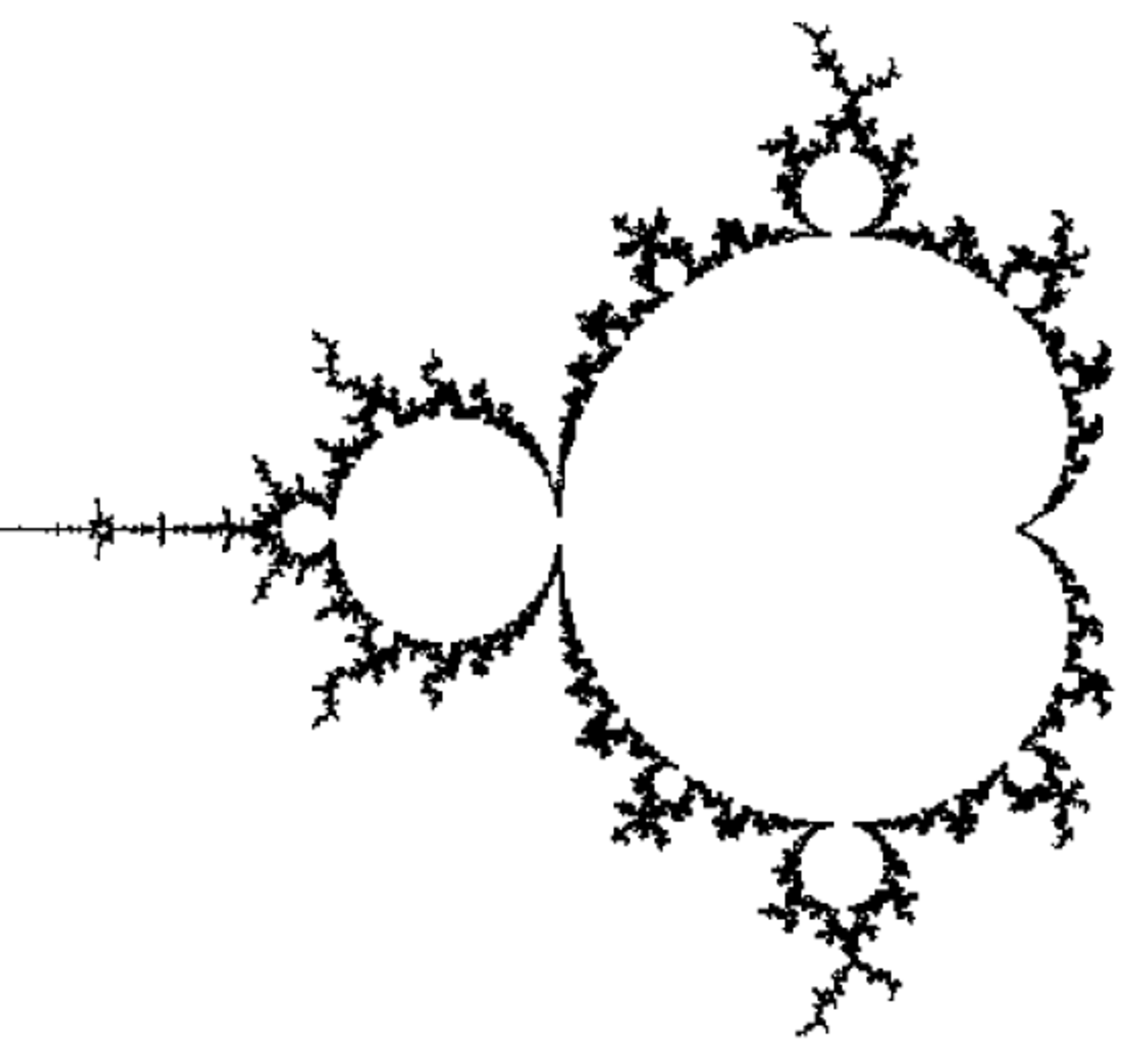
| La frontière a la même dimension que l'ensemble.. |
| 2 | 2 | certains ensembles de Julia |

| Pour des valeurs de c déterminées (sur la frontière de l'ensemble de Mandelbrot), l'ensemble de Julia a pour dimension 2.. |
| 2 | 2 | Courbe de Sierpiński |
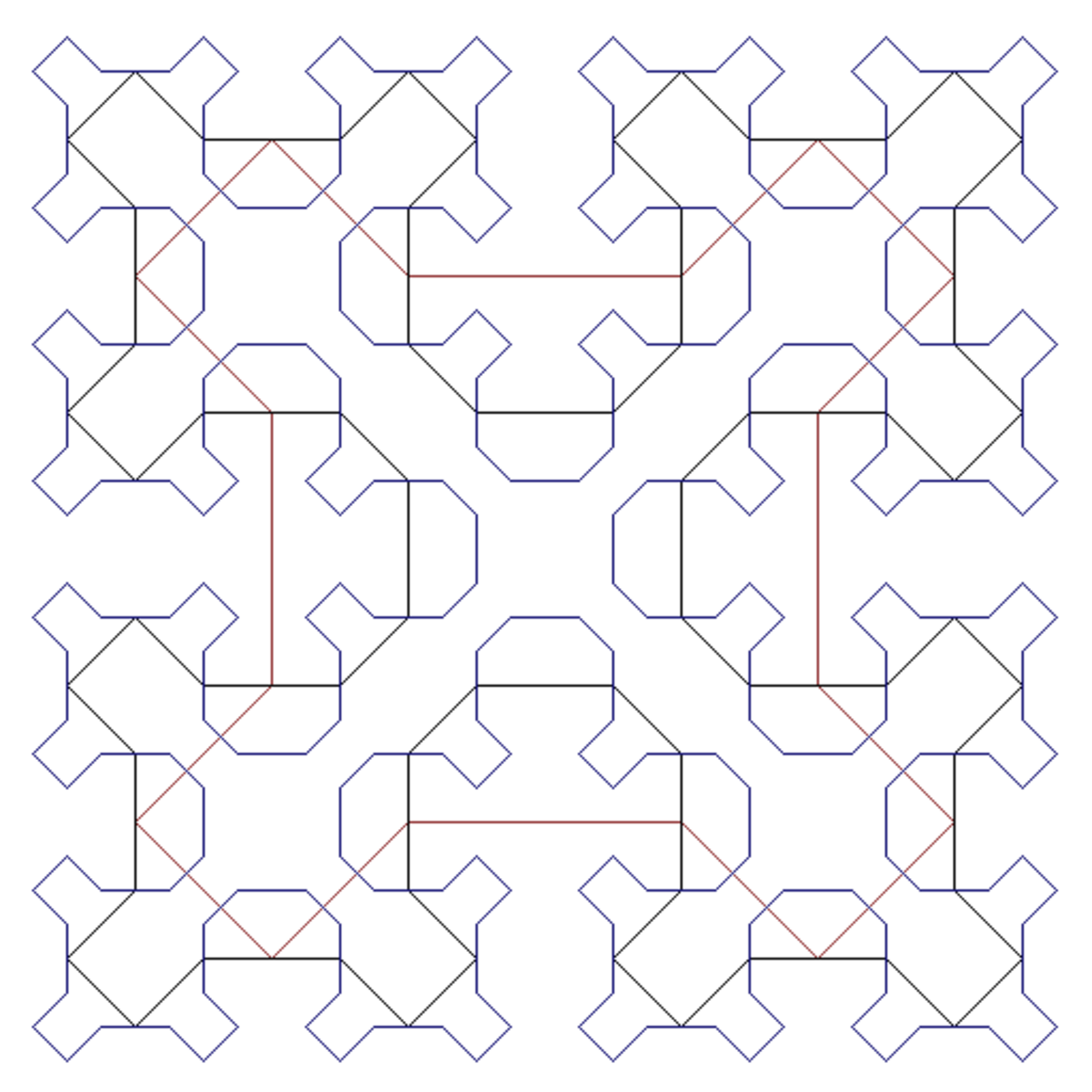
| Toute courbe remplissant l'espace possède une dimension de Hausdorff δ = 2. |
| 2 | 2 | Courbe de Hilbert |
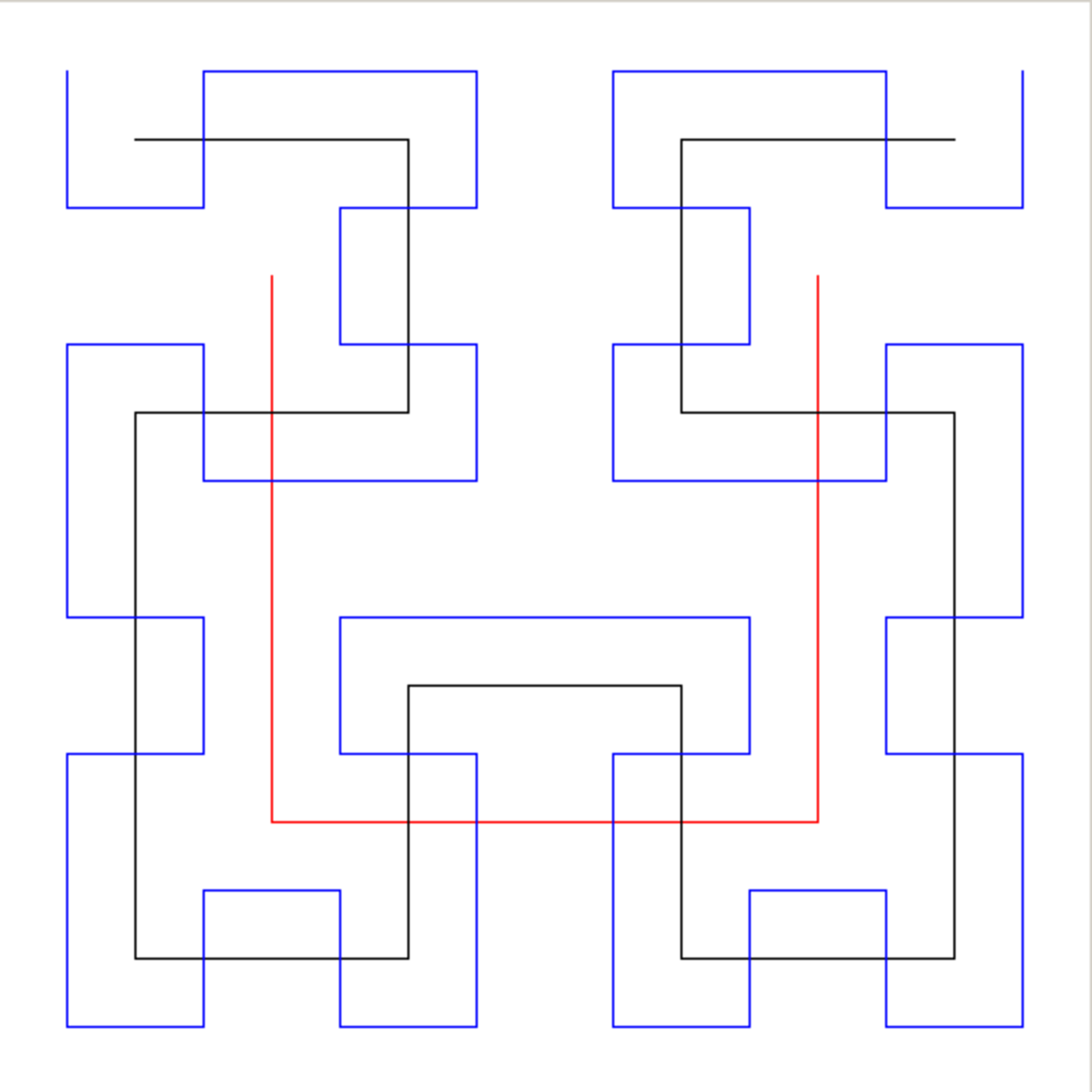
| Peut être étendue à trois dimensions. |
| 2 | 2 | Courbe de Peano |
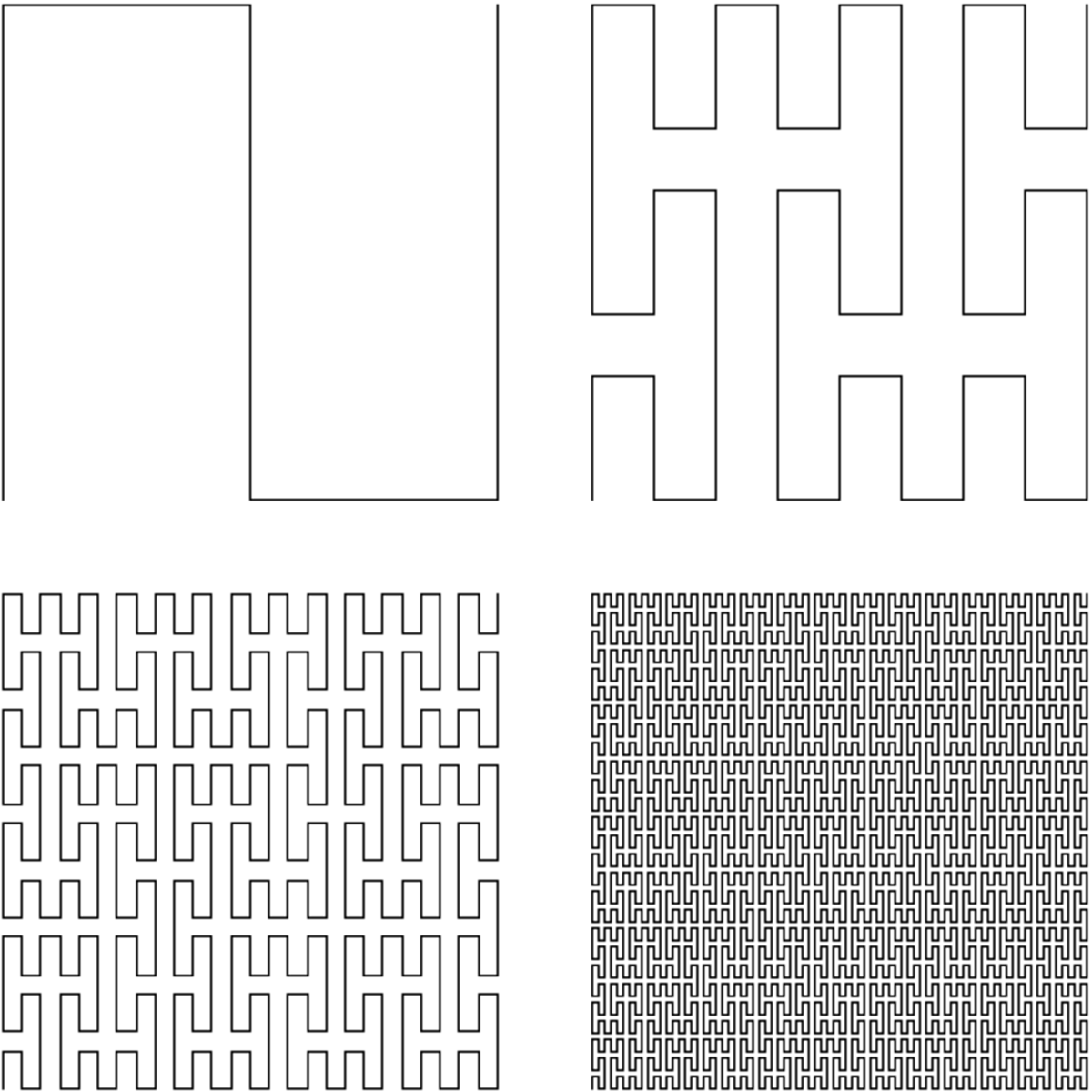
| et une famille de courbes de construction similaire, dont les courbes de Wunderlich. |
| 2 | 2 | Courbe de Moore |

| Peut être étendue à 3 dimensions. |
| 2 | 2 | Courbe de Lebesgue |

| Contrairement aux courbes ci-dessus, celle-ci est presque partout différentiable. Un deuxième type de courbe 2D a également été défini. Cette courbe peut être étendue en 3D avec une dimension fractale de 3.. |
|
| 2 | Courbe du dragon | Sa frontière a une dimension fractale de 1,5236 (Cf.Chang & Zhang) | |
| 2 | Courbe "Terdragon" |

| L-System : F→ F+F-F ; angle=120°. | |
|
| 2 | T-square |
| |
|
| 2 | Courbe de Peano-Gosper |

| Sa frontière est l'île de Gosper. |
| Solution de
| 2 | Courbe remplissant le flocon de Koch |
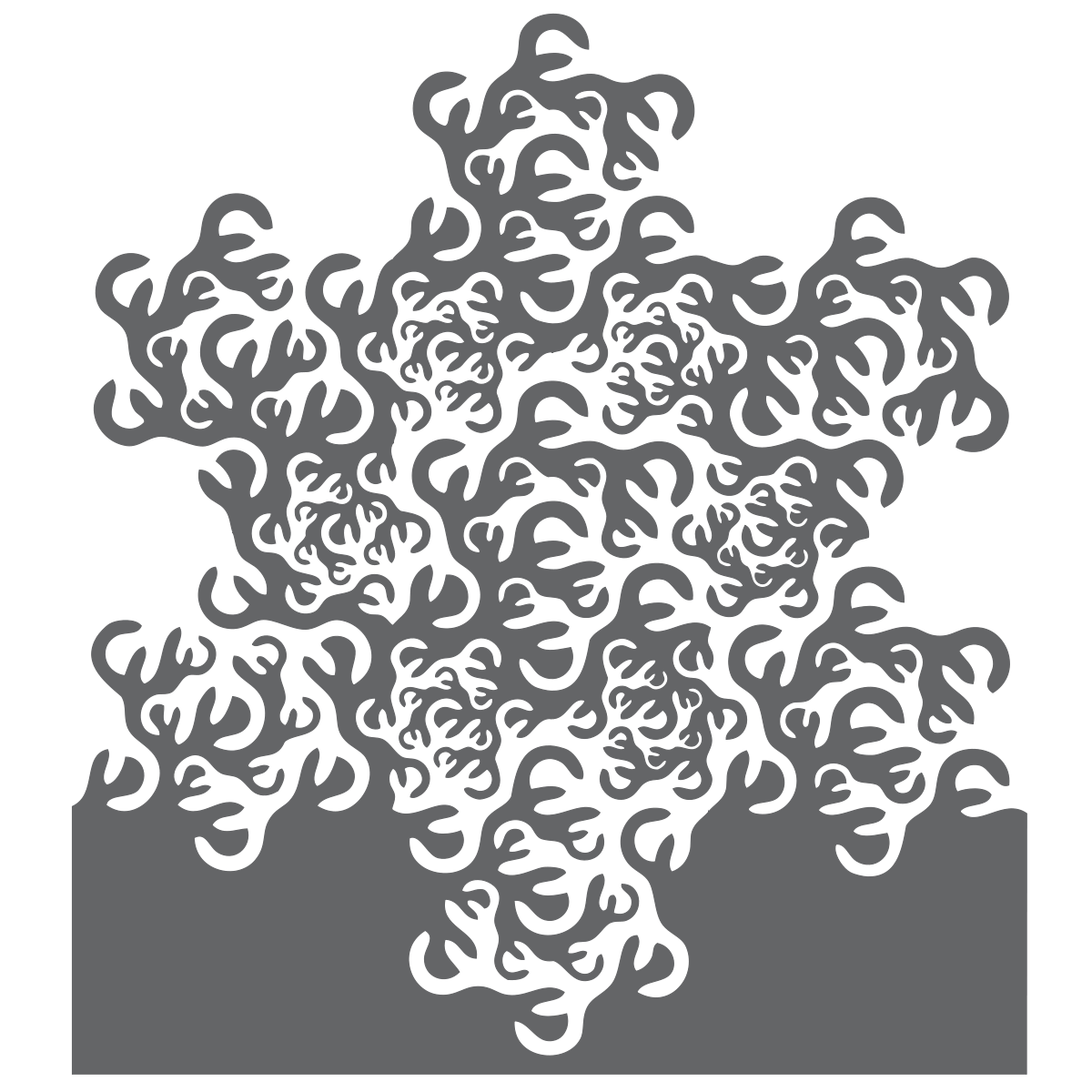
| Proposée par Mandelbrot en 1982, elle remplit le flocon de Koch. Elle est basée sur 7 similitudes de rapport 1/3 et 6 similitudes de rapport
|
|
| 2 | Tétraèdre de Sierpinski |
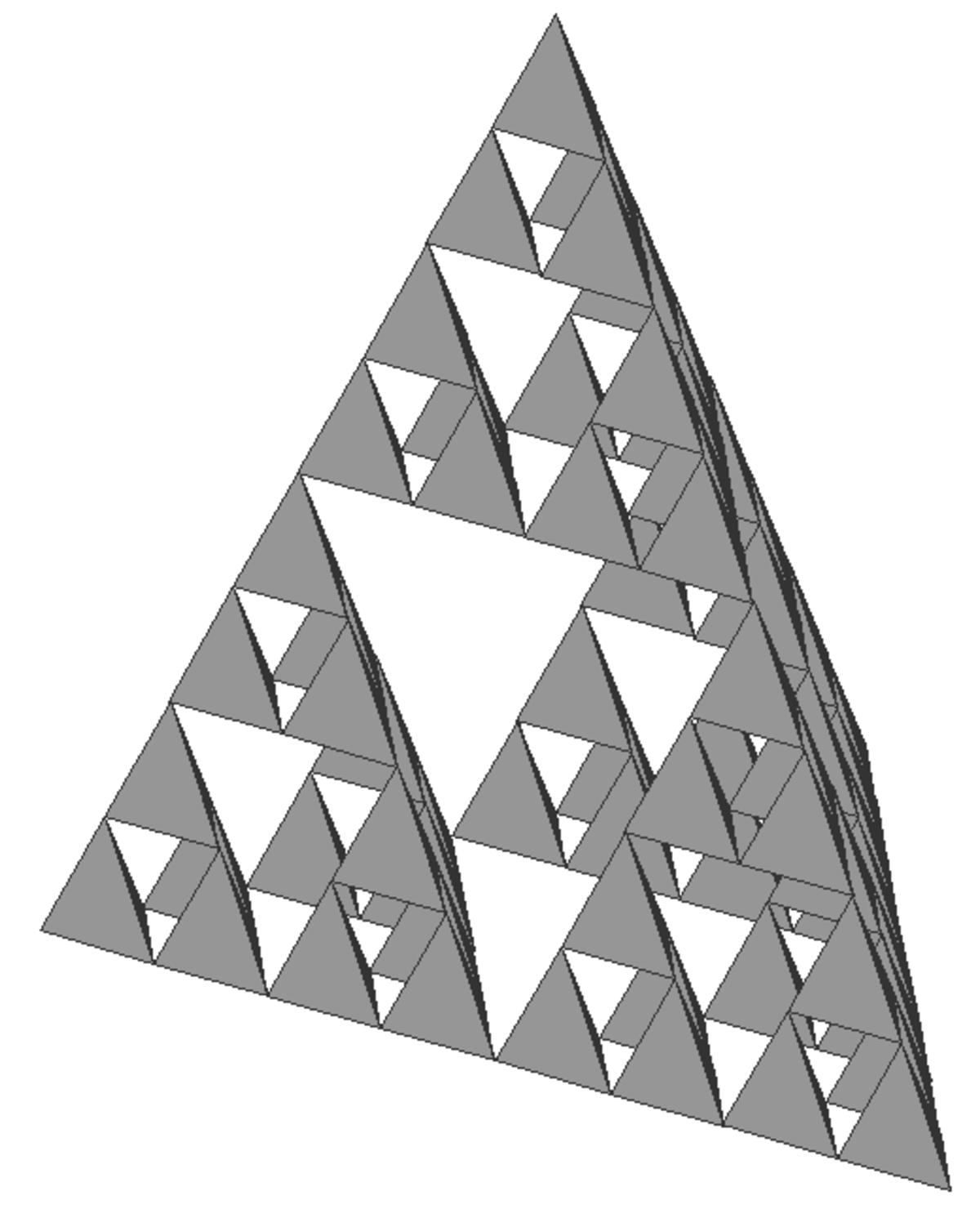
| Conséquence de sa dimension 2, sa surface reste inchangée d'itération en itération, et ce, jusqu'à l'infini. |
|
| 2 | Fractale H |
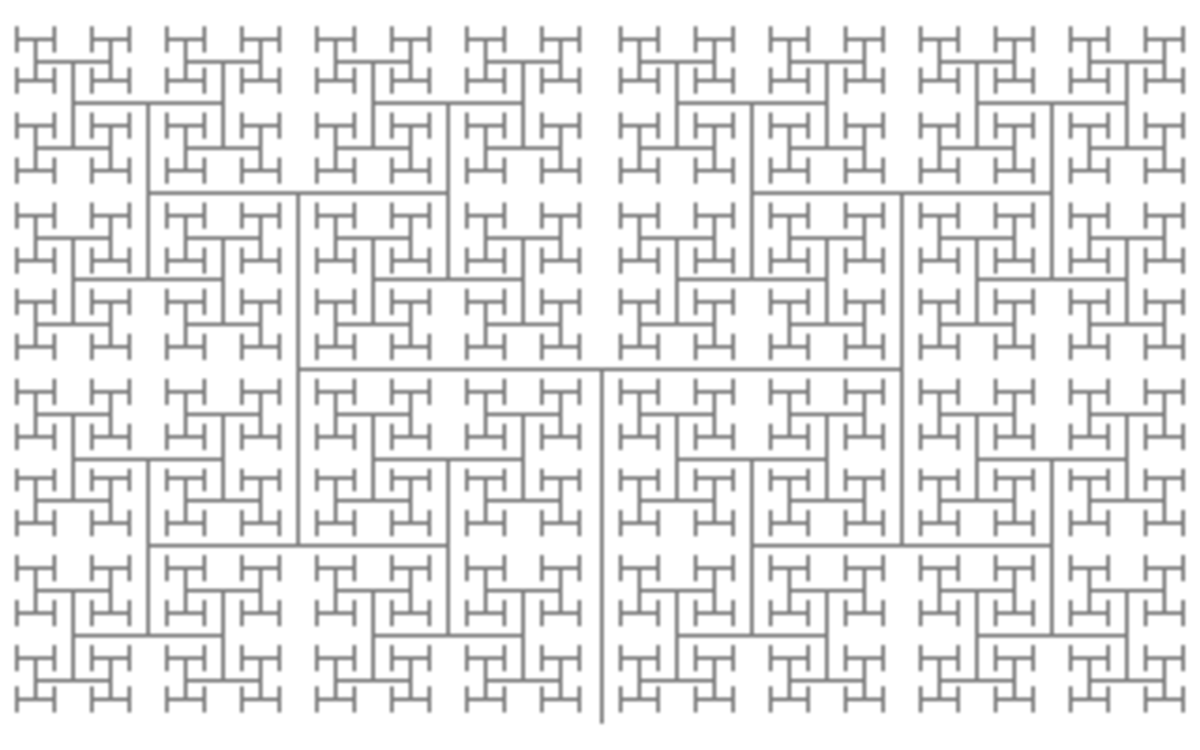
| Également, l'arbre de Mandelbrot, qui a une structure similaire. |
|
| 2 | Arbre de Pythagore |

| Chaque carré génère deux carrés de côté réduit de racine(2)/2. |
|
| 2 | Fractale en croix grecque |

| Chaque segment est substitué par une croix formée de quatre segments. |
2 < δ < 3
| δ (val. exacte) | δ (val. approchée) | Nom | Illustration | Remarques |
|---|---|---|---|---|
| Mesuré | 2.01 +-0.01 | Attracteur de Rössler |
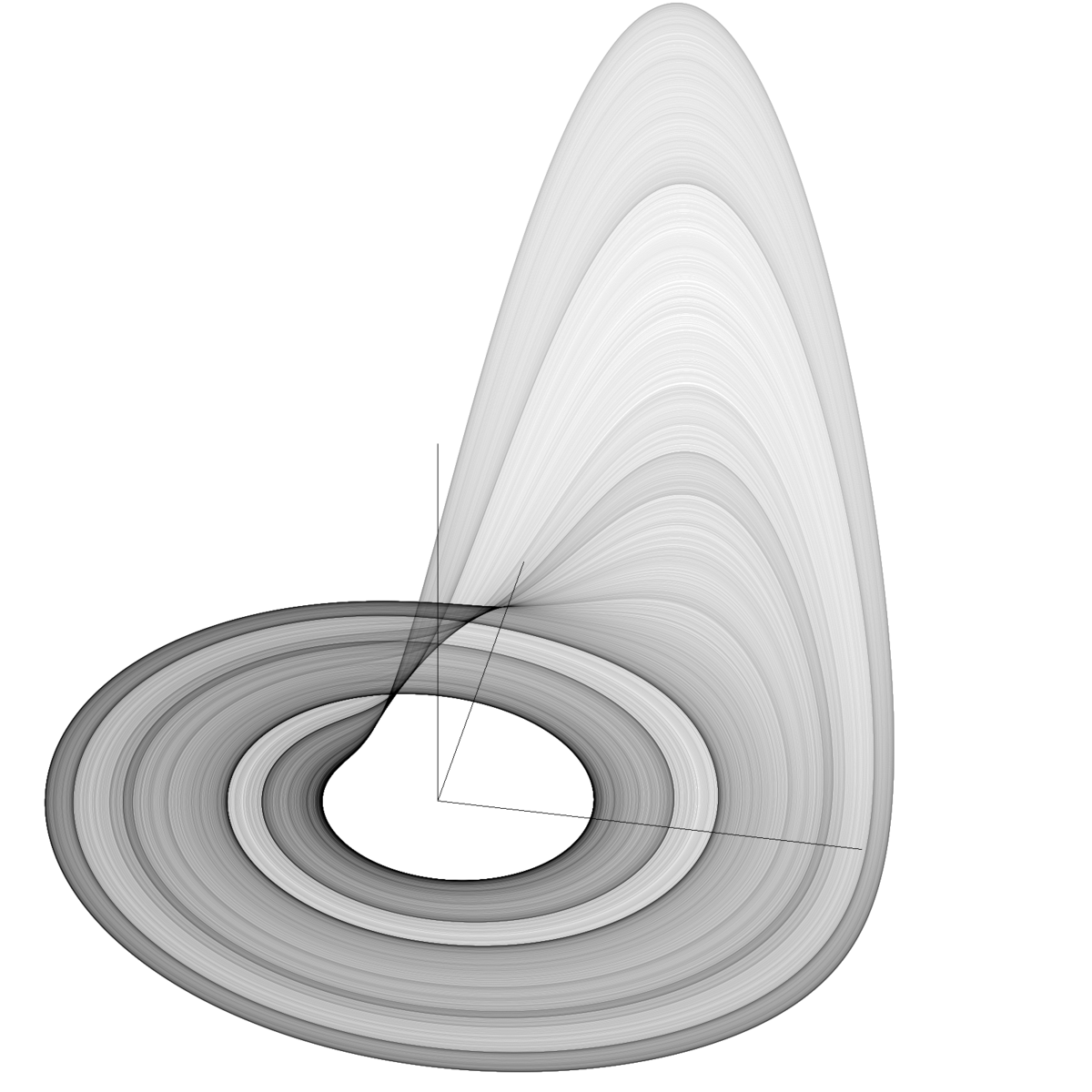
| La dimension fractale de l'attracteur de Rössler est légèrement supérieure à 2. Pour a=0,1, b=0,1, et c=14 elle est estimée entre 2,01 et 2,02.. |
| Mesuré | 2.06 +-0.01 | Attracteur étrange de Lorenz |

| Pour les paramètres de l'attracteur: v=40,σ=16 et b=4. |
| 2,3296 | Dodécaèdre fractal |

| Chaque dodécaèdre est substitué par 20 dodécaèdres. | |
|
| 2,33 | Surface quadratique de Koch en trois dimensions de type 1 |
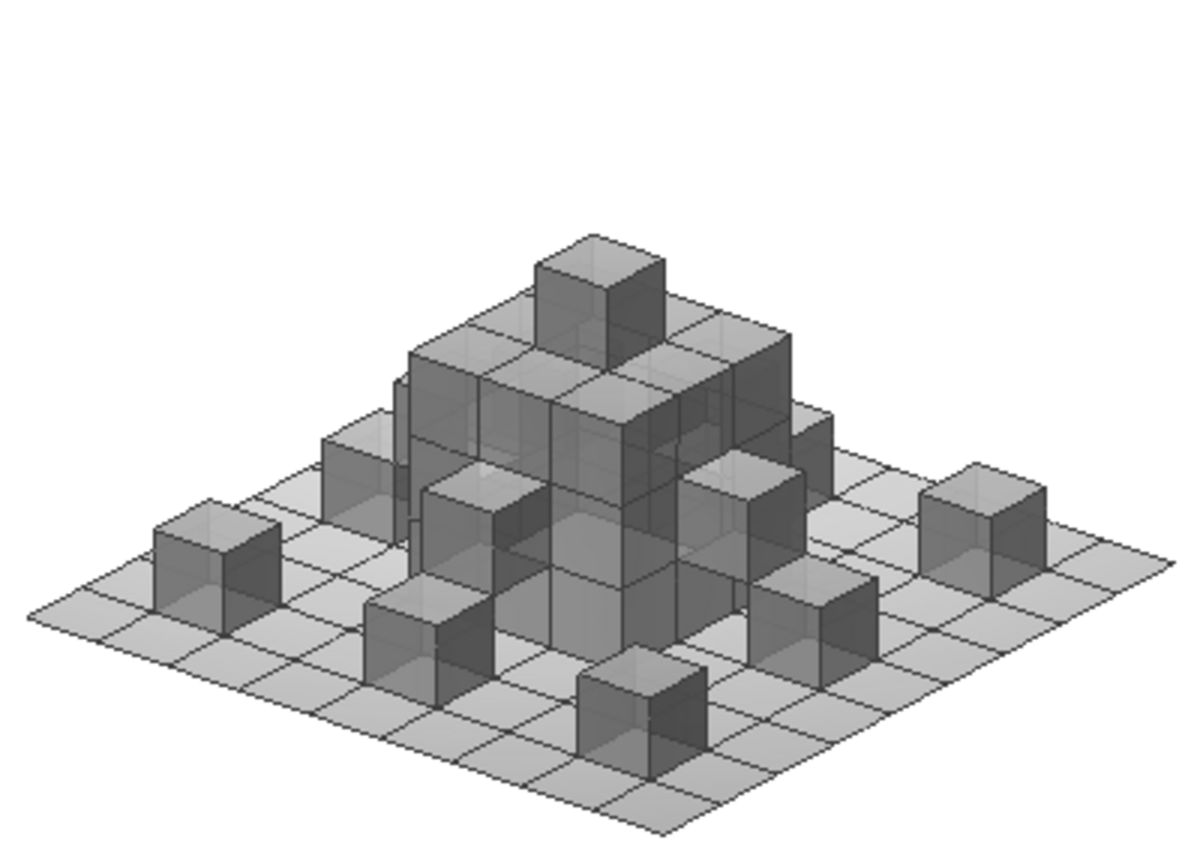
| Extension en trois dimensions de la courbe quadratique de Koch en deux dimensions de type 1 (la figure illustre la deuxième itération). |
| 2,47 | Interstices des sphères apolloniennes |

| Baderne d'Apollonius en trois dimensions. Modélise la mie de pain ou l'éponge. Dimension calculée par M. Borkovec, W. De Paris et R. Peikert. | |
|
| 2,50 | Surface quadratique de Koch en trois dimensions de type 2 |
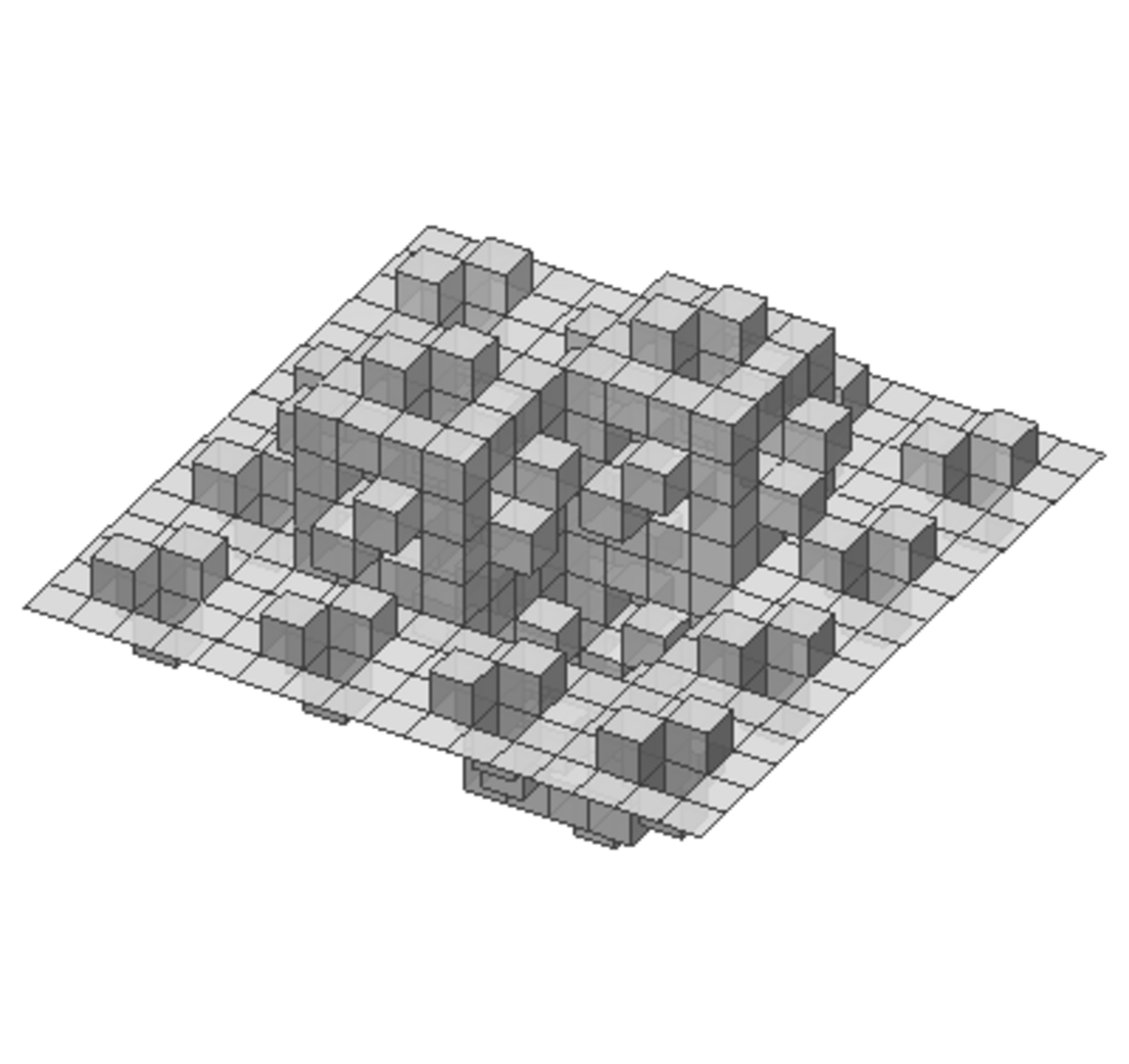
| Extension en trois dimensions de la courbe quadratique de Koch en deux dimensions de type 2 (la figure illustre la deuxième itération). |
|
| 2,5237 | Hypercube de Cantor | pas de représentation possible | Ensemble de Cantor en 4 dimensions. D'une manière générale, dans un espace de dimension n, l'ensemble de Cantor a une dimension fractale égale à
|
|
| 2,5819 | Icosaèdre fractal |
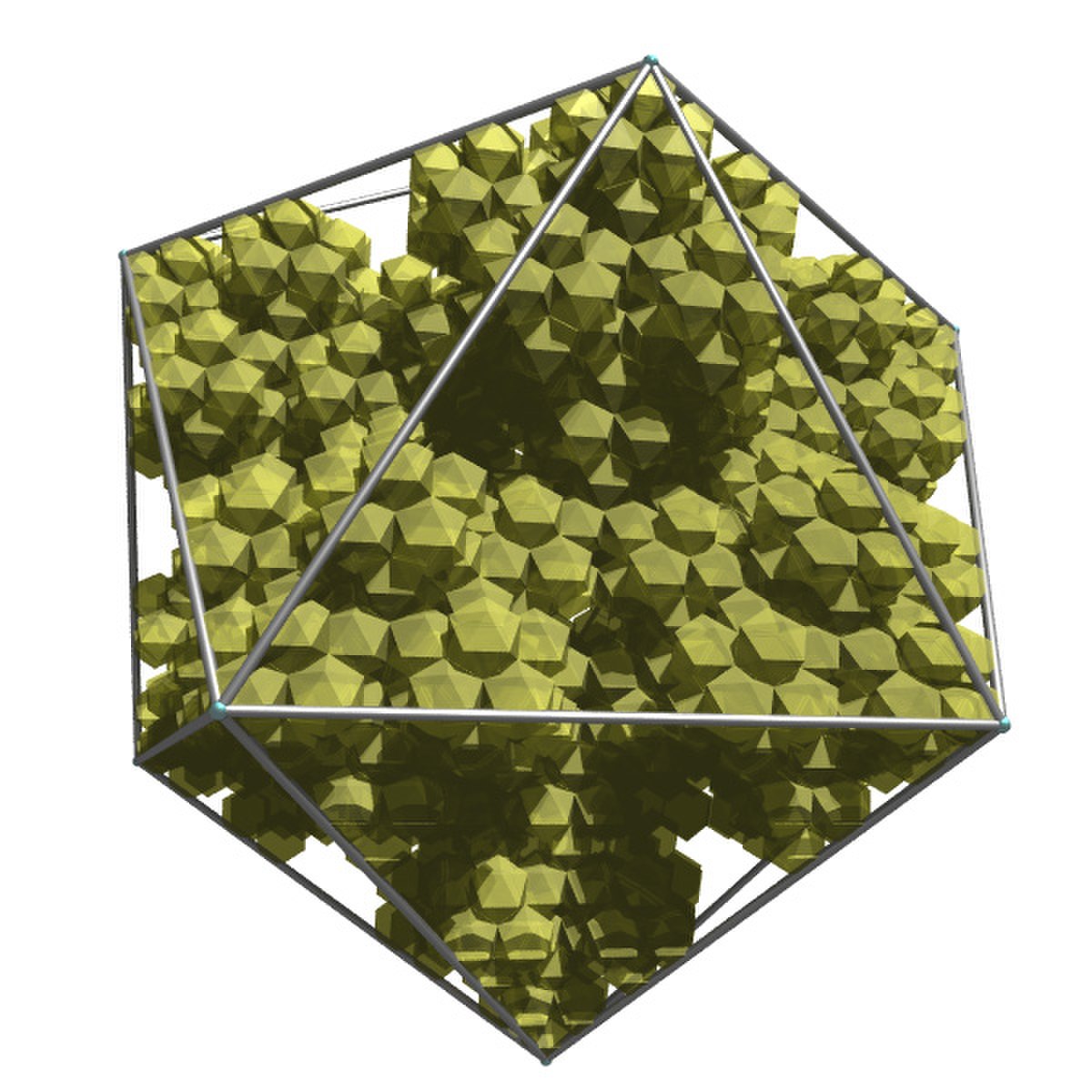
| Chaque icosaèdre est substitué par 12 icosaèdres. |
|
| 2,5849 | Octaèdre fractal |

| Chaque octaèdre est substitué par 6 octaèdres. |
|
| 2.5849 | Surface de Koch |
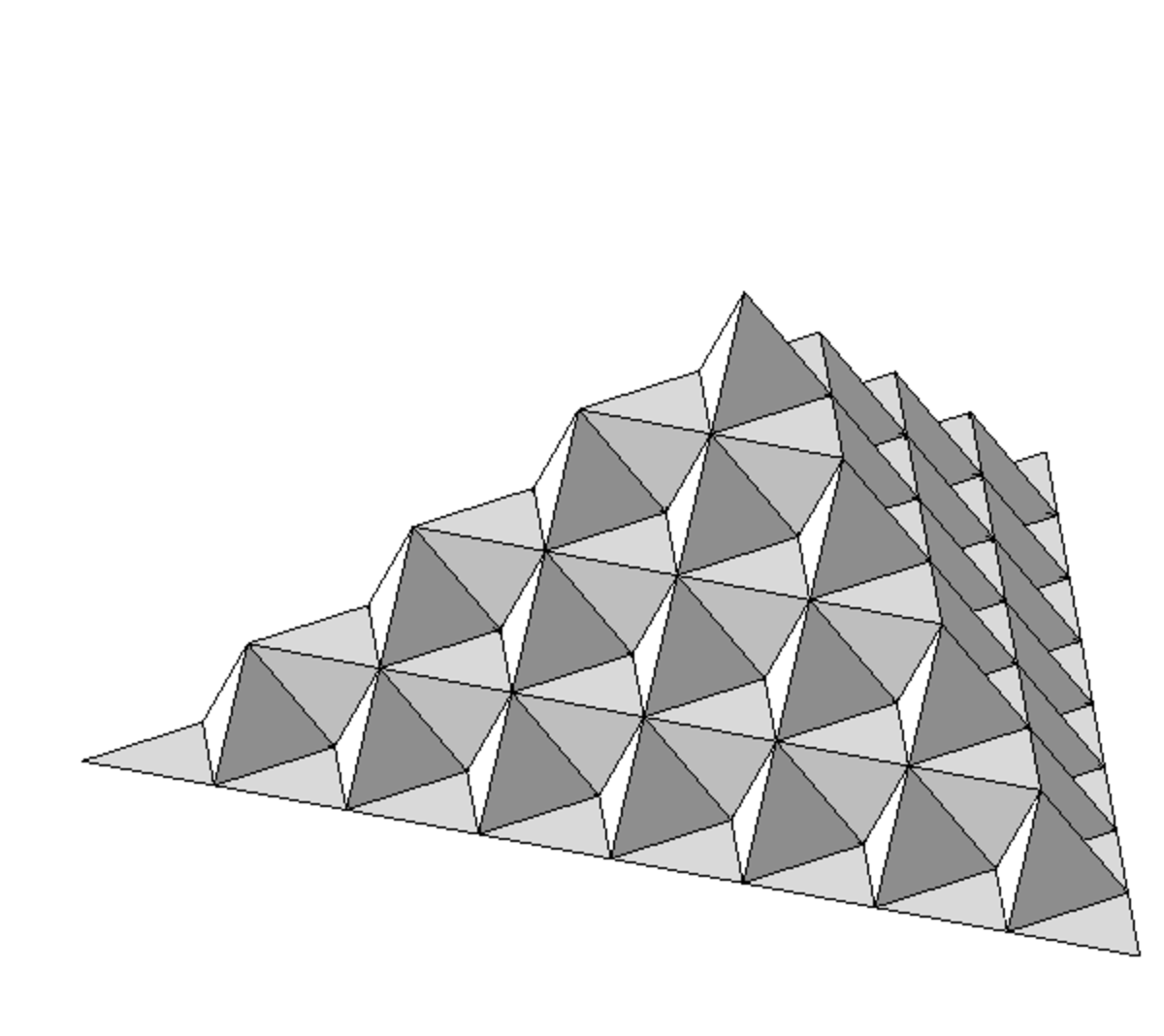
| Chaque triangle équilatéral est remplacé par 6 triangles deux fois plus petits. Extension en 2 dimensions de la courbe de Koch. |
|
| 2,59 | Fractale en croix grecque en trois dimensions |
| Chaque segment est substitué par une croix en trois dimensions formée de 6 segments. Extension en trois dimensions de la croix en deux dimensions. |
|
| 2,7268 | Éponge de Menger |

| Sa surface a une dimension fractale de
|
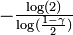
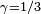
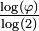
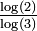
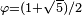
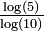
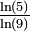
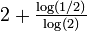
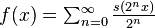
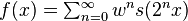
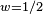
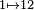
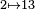
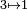
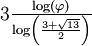
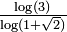
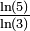
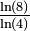
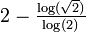
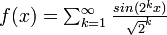
![\scriptstyle{f : [0,1] \to \mathbb{R}}](https://static.techno-science.net/illustration/Definitions/autres/0/0a248566ccd0c470073e1ce95e8f32e6_4903a7b62732c7734f025303b43c7cc3.png)
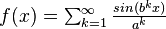
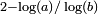
![\textstyle{\frac{\log\left(\frac{1+\sqrt[3]{73-6\sqrt{87}}+\sqrt[3]{73+6\sqrt{87}}}{3}\right)} {\log(2)}}](https://static.techno-science.net/illustration/Definitions/autres/b/b20412764066b5d7378580b90852dfd7_e93f4c58d30820910146788d477f0843.png)
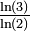
![\textstyle{\frac{\log{\varphi}}{log{\sqrt[\varphi]{\varphi}}}}](https://static.techno-science.net/illustration/Definitions/autres/d/d47514827f777a573813603117501196_62576c4234c0ffedfdf8d66dd9964401.png)

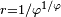

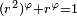
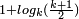
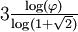
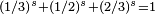
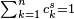
![\scriptstyle {z_{n+1} = a + bz_n exp[i[k - p/(1 + \lfloor z_n \rfloor^2)]]}](https://static.techno-science.net/illustration/Definitions/autres/7/777e0d20cd1bfa44a5965504a196e761_c2f435d07d9dbef332b341bdff0f532f.png)