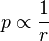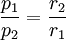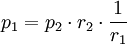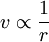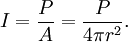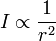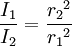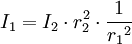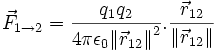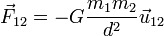Loi en carré inverse - Définition

Introduction

Ce diagramme montre le fonctionnement de la loi en carré inverse. Les lignes représentent le flux émanant de la source. Le nombre total de lignes de flux dépend de l'intensité de la source et est constant avec l'accroissement de la distance. Une densité plus importante de lignes de flux (lignes par unité de surface) est la traduction d'un champ plus intense. La densité de flux est inversement proportionnelle au carré de la distance à la source car l'aire d'un secteur de disque s'accroit avec le carré de son rayon. L'intensité du champ est donc inversement proportionnelle au carré de la distance à la source.

En physique, une loi en carré inverse est une loi physique postulant qu'une quantité physique (énergie, force, ou autre) est inversement proportionnelle au carré de la distance de l'origine de cette quantité physique.

Cette loi fut d'abord suggérée par l'astronome français Ismaël Boulliau, puis mise en forme par Isaac Newton après que Robert Hooke lui eut proposé l'idée dans une lettre. Robert Hooke accusa plus tard Newton de plagiat.

Champs d'application

En acoustique

La loi du carré inverse se trouve en propagation du son lorsqu'il est s'agit de donner son intensité à une distance donnée d'une source sonore.

La pression sonore d'un front d'onde sphérique irradiant d'un point source décroit d'un facteur ½ lorsque la distance r est doublée, ou, si elle est exprimée en dB, perdra 6,02 dB. Le comportement de cette pression n'est donc pas en carré inverse, mais simplement inverse :

Cependant, la remarque est également valable pour la vitesse particulaire v qui est en phase avec la pression sonore instantanée p.

La composante quadratique de la vitesse particulaire est dans un déphasage de 90° avec la pression sonore seulement en champ proche, ce qui ne contribue pas à l'énergie moyennée temporellement (i.e. intensité sonore). Cette composante se trouve être en carré inverse. L'intensité sonore est le produit de la valeur efficace de la pression sonore et de celle de la vitesse particulaire (composante en phase), les deux étant proportionnelles inverses. L'intensité suit donc une loi en carré inverse comme indiqué ci-dessous :

.

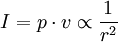
Cette loi en carré inverse a trait à l'intensité sonore. Cependant, les pressions sonores étant plus accessibles à la mesure, cette loi est parfois qualifiée de « loi en inverse de la distance ».

En électromagnétisme

Généralités

L'intensité (ou éclairement lumineux ou irradiance) de la lumière ou d'autres ondes linéaires se propageant à partir d'une source ponctuelle (énergie par unité de surface perpendiculaire à la source) est inversement proportionnelle au carré de la distance à la source, ce qui fait qu'un objet (de même taille) placé deux fois plus loin recevra seulement un quart de l'énergie émise (pour la même période).
Plus généralement, l'irradiance, i.e. l'intensité (ou puissance par unité de surface dans la direction de propagation, d'un front d'onde sphérique varie en raison inverse de la distance à la source (en postulant qu'il n'y ait pas de pertes dues à l'optique ou à la diffusion).
Ainsi par exemple, l'intensité de la lumière émise par le Soleil est de 9140 watts par mètre carré à la distance de Mercure (0,387 UA), mais seulement de 1370 W/m² à la distance de la Terre (1 UA), une multiplication par trois environ de la distance résultant en une division par neuf environ de l'intensité lumineuse.
Les photographes et les éclaireurs de théâtre utilisent cette loi afin de déterminer la localisation optimale des sources de lumière afin que le sujet soit convenablement éclairé. Cette loi est aussi particulièrement importante en radiographie et dans la planification des traitements en radiothérapie.

Exemple

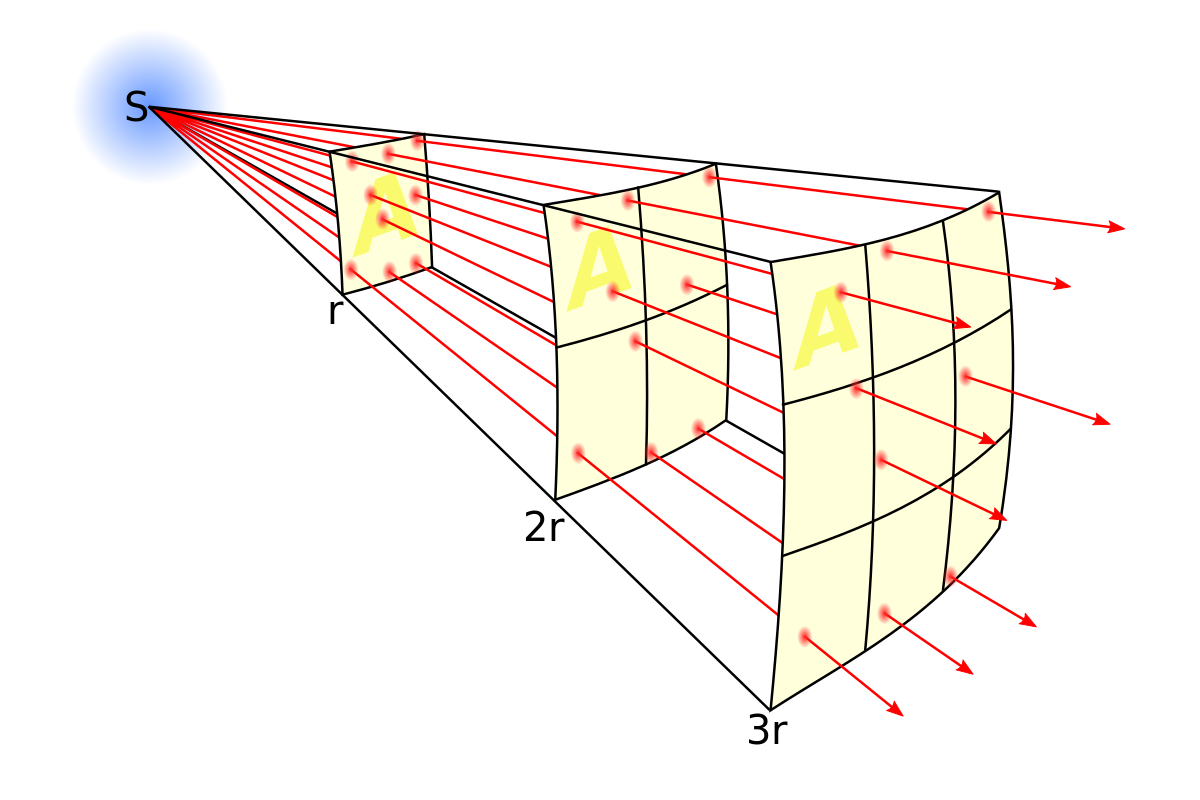
Prenons comme exemple la puissance totale irradiée à partir d'un point source (comme une antenne isotrope), notée P. Pour des distances à la source importantes (relativement à la taille de la source), cette puissance est distribuée sur des surfaces sphériques de plus en plus importantes lorsque la distance s'accroît. Puisque la superficie d'une sphère de rayon r est A = 4πr², l'intensité I de la radiation à la distance r est :

L'énergie ou l'intensité décroît d'un facteur ¼ lorsque la distance r est doublée. C'est la raison fondamentale pour laquelle l'intensité d'une radiation, qu'elle soit électromagnétique ou acoustique, suit une loi en carré inverse, et ceci au moins dans un contexte idéalement tridimensionnel (une propagation en deux dimensions suivrait une loi inverse de la distance et en une dimension, l'onde plane resterait constance en amplitude alors même que la distance à la source change).

En électrostatique

En électrostatique, la force agissant sur un objet chargé par un autre objet chargé est une force centrale dont l'expression est la suivante :

dans laquelle ε₀=8,854·10^-12 F·m^-1 est une constante universelle appelée permittivité électrique du vide, et est le vecteur position qui relie le premier corps au deuxième, les lettres q désignant les charges des deux objets.

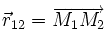
En mécanique (gravitation)

Dans le cadre de la mécanique newtonienne, la force de gravitation s'exprime comme une force centrale dépendante de l'inverse du carré de la distance à l'objet exerçant l'attraction de manière tout à fait analogue à la loi de Coulomb :

• étant la force gravitationnelle exercée par le corps 1 sur le corps 2 (en newton ou m.kg.s^-2) ;
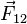
• G, la constante gravitationnelle, qui vaut 6,6742×10^-11 N.m².kg^-2 (ou m³.kg^-1.s^-2)
• m₁ et m₂, les masses des deux corps en présence (en kilogrammes) ;
• d, la distance entre les deux corps (en mètres) ;
• est un vecteur unitaire dirigé du corps 1 vers le corps 2 ;
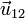
• le signe – indique que le corps 2 est attiré par le corps 1.

Il convient de noter que ce type de forces (force de gravitation et force électrostatique) génèrent des trajectoires qui sont ce qu'on appelle en mathématiques des coniques (ellipses, paraboles et hyperboles), ce qui se retrouve en particulier dans les mouvements des objets célestes lorsque les effets relativistes sont peu perceptibles.