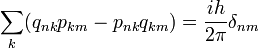Mécanique matricielle - Définition

Prix Nobel

En 1928, Albert Einstein avait proposé Heisenberg, Born, et Jordan pour le prix Nobel de physique, mais cela n'aboutit pas. L'annonce du prix Nobel de 1932 fut différée jusqu'en novembre 1933 : Heisenberg en fut le lauréat de 1932 « pour la création de la mécanique quantique, l'application de laquelle ayant, inter alia, conduit à la découverte de la forme allotropique de l'hydrogène » alors qu'Erwin Schrödinger et Paul Dirac furent les lauréats de l'édition 1933 pour la « découverte de nouvelles formes productives de la théorie atomique ». On peut cependant se poser la question suivante : pourquoi Born ne fut pas lauréat du prix en 1932 aux côtés d'Heisenberg ? Bernstein fournit quelques spéculations sur ce fait. L'une d'entre elles est le fait que Jordan rejoignit le parti nazi le 1^er mai 1933 et devint SA. Cet engagement et le lien de Jordan avec Born auraient alors compromis les chances de ce dernier. Bernstein indique aussi que lorsque Born obtint le prix Nobel en 1954, Jordan était toujours vivant, et que ce prix fut décerné pour l'interprétation statistique de la mécanique quantique, attribuée au seul Born.

La réaction d'Heisenberg envers Born lorsqu'il reçut le prix en 1932 et celle lorsque Born reçut le prix en 1954 sont aussi instructives sur le fait que Born aurait dû recevoir le prix Nobel avec Heisenberg en 1932. Le 25 novembre 1933, Born reçut une lettre de Heisenberg dans laquelle il disait avoir attendu pour l'écrire en raison d'« mauvaise conscience » due au fait qu'il avait reçu seul le prix « pour un travail effectué à Göttingen en collaboration – vous, Jordan et moi ». Heisenberg en vint à indiquer que la contribution de Born et Jordan à la mécanique quantique ne pouvait être changée par « une mauvaise décision extérieure ». En 1954, Heisenberg écrivit un article honorant Max Planck pour sa sagacité en 1900. Dans l'article, Heisenberg créditait Born et Jordan pour la formulation mathématique finale de la mécanique matricielle et appuya sur l'importance de leurs contributions à la mécanique quantique, qui ne furent pas « reconnue de manière adéquate par le grand public ».

Développement ultérieur

Lorsqu'elle fut introduite par Werner Heisenberg, Max Born et Pascual Jordan en 1925, la mécanique matricielle ne fut pas immédiatement acceptée et fut source de controverse importante. Le concept plus tardif de fonction d'onde présenté par Schrödinger lui était préféré.

Une des raisons de cette méfiance était que la formulation d'Heisenberg se faisait dans le langage des matrices, peu familier aux physiciens à l'époque, alors que la formulation de Schrödinger se basait sur des équations d'ondes, bien mieux connues. Mais il existait aussi une raison sociologique plus profonde. La mécanique quantique avait été développée par deux voies différentes, une sous la direction d'Albert Einstein et l'autre sous la direction de Niels Bohr (dite École de Copenhague). Le premier mettait l'accent sur la dualité onde-corpuscule, alors que le second s'attachait plutôt aux états d'énergie discrets et aux sauts quantiques. Louis de Broglie avait montré comment reproduire les états discrets d'énergie dans le formalisme d'Einstein dans laquelle la condition quantique est intrinsèque à la condition ondulatoire, et cela laissait penser aux tenants de l'école d'Einstein que tous les aspects discrets de la mécanique quantique pouvaient se fondre dans la continuité de la mécanique ondulatoire.

La mécanique matricielle, d'un autre côté, était issue de l'école de Bohr. Les tenants de Bohr n'appréciaient pas les modèles physiques décrivant les électrons comme des ondes, ou quoi que ce soit de ressemblant, préférant s'attacher aux quantités directement liées aux expériences.

En physique atomique, la spectroscopie produisait des données observables sur les transitions atomiques dues aux interactions entre atomes et quanta de lumière. L'école de Bohr indiquait que seules ces quantités qui étaient en principe mesurables par spectroscopie devaient apparaître dans la théorie. Ces quantités incluent les niveaux énergétiques et leurs intensités mais pas la localisation exacte d'une particule dans son orbite de Bohr. Il est très difficile d'imaginer une expérience qui pourrait déterminer si un électron dans l'état fondamental d'un atome d'hydrogène est à la droite ou à la gauche du noyau. Le fait que de telles questions ne pouvaient se voir apporter de réponse était une conviction profonde.

La formulation matricielle fut construite sur la prémisse que toutes les observables physiques sont représentables par des matrices dont les éléments sont indexés par deux niveaux d'énergie distincts. L'ensemble des valeurs propres de la matrice pouvait également être compris comme l'ensemble de toutes les valeurs possibles des observables. Les matrices d'Heisenberg étant hermitiennes, les valeurs propres sont réelles.

Si une observable est mesurée et que le résultat est une des valeurs propres, le vecteur propre correspondant est l'état du système immédiatement après la mesure. L'action de mesure en mécanique matricielle « fait s'effondrer » l'état du système. Si l'on mesure deux observables simultanément, l'état du système devrait s'effondrer vers un vecteur propre commun aux deux observables. La plupart des matrices n'ayant pas de vecteur propre commun, la plupart des observables ne peuvent être mesurée en même temps : cela constitue le principe d'incertitude.

Si deux matrices partagent leurs vecteurs propres, elles peuvent être diagonalisées simultanément. Dans les bases dans lesquelles elles sont simultanément diagonales, leur produit ne dépend pas de l'ordre de multiplication, le produit de matrices diagonales se résumant à un produit de nombres. Le principe d'incertitude est donc une conséquence de la non-commutativité du produit de deux matrices A et B, AB-BA n'étant pas nécessairement la matrice nulle. La fameuse relation de commutation de la mécanique matricielle :

montre qu'il n'y a pas d'états ayant simultanément une position et une quantité de mouvements définies. Mais le principe d'incertitude (aussi appelé complémentarité par Bohr) est valable pour la plupart des autres paires d'observables. Ainsi par exemple, l'énergie ne commute pas avec la position non plus, il est donc impossible de déterminer précisément à la fois la position et l'énergie d'un électron dans un atome.