Mécanique matricielle - Définition
La liste des auteurs de cet article est disponible ici.
Résultats consécutifs
La mécanique matricielle évolua rapidement vers la mécanique quantique moderne, et donna des résultats physiques intéressants sur les spectres d'atomes.
Mécanique ondulatoire
Jordan avait noté que les relations de commutation font que p agit comme un opérateur différentiel, et parvint presque à formuler l'équation de Schrödinger.
L'identité :
permet l'évaluation du commutateur de p avec une puissance quelconque de x, et cela implique que :
qui, par linéarité, implique à son tout qu'un commutateur p différentie tout fonction matricielle analytique de x. En postulant que les limites sont définies avec précision, cela s'étend à des fonctions arbitraires, mais cette extension n'a pas besoin d'être conduite explicitement jusqu'à ce qu'un certain degré de rigueur mathématique soit requis.
x étant une matrice hermitienne, elle doit être diagonalisable, et il est clair à partir de la forme éventuelle de p que tout nombre réel peut être une valeur propre. Cela participe de la subtilité mathématique, puisqu'il existe un vecteur propre distinct pour chaque point de l'espace. Dans la base dans laquelle x est diagonale, un état arbitraire peut être écrit comme une superposition d'états avec les valeurs propres x :
et l'opérateur x mutiplie chaque vecteur d'onde par x.
En définissant un opérateur linéaire D qui différentie ψ :
et en notant que :
l'opérateur -iD obéit à la même relation de commutation que p. La différence entre p et -iD doit commuter avec x.
ce qui permet de le diagonaliser simultanément à x : sa valeur agissant sur tout état propre de x est une fonction f de la valeur propre x. Cette fonction doit être réelle, p et -iD étant hermitiens :
Chaque état |x> étant décalé d'une phase f(x), cela conduit à, en redéfinissant la phase de la fonction d'onde :
rotating each state |x> by a phase f(x), that is, redefining the phase of the wavefunction:
l'opérateur iD est redéfini par :
ce qui signifie que dans une base ayant subi une rotation, p est égal à -iD. Il y a donc toujours une base pour les valeurs propres de x où l'action de p sur n'importe quelle fonction d'onde est connue :
et le hamiltonien dans cette base est un opérateur différentiel linéaire sur les composants du vecteur d'état :
L'équation du mouvement pour le vecteur d'état est l'équation différentielle :
D étant un opérateur différentiel, il doit exister des valeurs propres de x au voisinage de toute valeur donnée afin de le définir de manière précise. Cela suggère que la seule possibilité est que l'espace des valeurs propres de x soit un espace réel, et que p soit identifié à iD à la rotation près. Afin d'être formulé rigoureusement, cela nécessite uen discussion approfondie sur l'espace limite des fonctions. Dans cet espace, le théorème de Stone-von Neumann s'applique : tous opérateurs x et p qui obéissent à des relations de commutations peuvent être construits pour agir sur l'espace des fonctions d'ondes, p étant un opérateur de dérivation. Cela implique qu'une représentation de Schrödinger est toujours possible.
Contrairement à l'approche de Schrödinger, la mécanique matricielle peut être étendue à tous les degrés de liberté de manière relativement simple. Chaque degré de liberté possède un opérateur x distinct et un opérateur p distinct, et la fonction d'onde est une fonction de toutes les valeurs propres possibles des variables x indépendantes et commutatives.
Cela signifie en particulier qu'un système de N particules interagissantes en 3 dimensions est décrit par un vecteur dont les composantes dans une base où tous les X sont diagonaux est une fonction mathématique d'un espace de dimension 3N qui décrit toutes les positions possibles, ce qui est un ensemble de valeurs bien plus important que N fonctions d'ondes tridimensionnelles dans un espace physique. Schrödinger parvint à la même conclusion de manière indépendante, et prouva par la suite l'équivalence entre son formalisme et celui d'Heisenberg.
La fonction d'onde étant une propriété du système dans son ensemble, et non d'une partie quelconque, la description en mécanique quantique n'est pas entièrement locale. La description de plusieurs particules peut être corrélée quantiquement, ou intriquée. Cette intrication conduit à des corrélations « étranges » entre particules distantes qui violent l'inégalité de Bell classique. Même si les particules peuvent occuper seulement deux positions, la fonction d'onde pour N particules nécessite 2N nombres complexes, un pour chaque configuration de positions, soit un nombre exponentiel en N de nombres. Simuler des systèmes quantiques numériquement nécessite donc des ressources très importantes. Cela suggère également qu'il pourrait être possible de trouver un système quantique de taille N qui calcul de manière physique les solutions aux problèmes requérant 2N bits pour être résolus, ce qui est une des motivations de recherche sur l'ordinateur quantique.
Théorie de la transformation
En mécanique classique, une transformation canonique des coordonnées de l'espace des phases est une tranformation qui conserve la structure des crochets de Poisson. Les nouvelles variables x' et p' ont tous deux les mêmes crochets de Poisson que les variables originales x et p. L'évolution temporelle est une transformation canonique, l'espace de phase pour tout instant étant juste un choix approprié de variables comme pour un espace de phase à tout autre instant.
Le flux hamiltonien est donc la transformation canonique canonique :
Le hamiltonien pouvant être une fonction arbitraire de x et p, il existe des transformations canoniques infinitésimales correspondant à chaque quantité classique G, où G est utilisée comme hamiltonien afin de générer un flux de points dans l'espace de phase pour un incrément temporel de s.
Pour une fonction générique A(x,p) de l'espace de phase, le changement infinitésimal à chaque pas ds sur la nappe est :
La quantité G est appelée générateur infinitésimal pour la transformation canonique.
En mécanique quantique, G est une matrice hermitienne, et les équations du mouvement sont des commutateurs :
Les mouvements canoniques infinitésimaux peuvent être intégrés formellement, de la même manière que l'équation du mouvement d'Heisenberg :
où U = eiGs et s sont des paramètres arbitraires. La définition d'une transformation canonique est un changement unitaire abritraire de base sur l'espace des vecteurs d'état. U est une matrice unitaire arbitraire, rotation complexe dans l'espace de phase.
Ces transformations laissent la somme du module au carré des composants de la fonction d'onde invariante, et transforme les états multiples les uns des autres (y compris les états multiples imaginaires les uns des autres) en états qui sont les mêmes multiples les uns des autres.
L'interprétation de ces matrices est qu'elles agissent comme générateurs de mouvements dans l'espace des états. Le mouvement généré par P peut être trouvé en résolvant l'équation du mouvement d'Heisenberg en utilisant P comme hamiltonien :
Il existe des translations de la matrice X qui ajoute un multiple de l'identité :
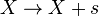
Lorsqu'une transformation, comme une rotation dans l'espace physique, commute avec le hamiltonien, la transformation est appelée une symétrie. Le hamiltonien exprimé en termes de coordonnées de rotation est le même que le hamiltonien original. Cela signifie que la modification du hamiltonien sous l'action du générateur infinitésimal L est nulle :
Il s'ensuit que la modification dans le générateur sous l'effet d'une translation temporelle est aussi nulle :
La matrice L est donc constante dans le temps. L'association des générateurs infinitésimaux de symétrie un à un et les lois de conservation furent tout d'abord découvertes par Emmy Noether pour la mécanique classique, où les commutateurs sont des crochets de Poisson mais l'argument reste le même.
En mécanique quantique, une transformation de symétrie unitaire donne une loi de conservation, la matrice U ayant la propriété suivante :
Il s'ensuit que UH = HU et que la dérivée temporelle de U est nulle.
Les valeurs propres des matrices unitaires sont des phases pures, ce qui implique que la valeur d'une quantité conservé unitairement est un nombre complexe de module unité, et non un réel. Une autre façon de le dire est qu'une matrice unitaire est l'exponentielle de i fois une matrice hermitienne, ce qui implique que la quantité réelle additive conservée, la phase, n'est bien définie qu'à un multiple entier de 2π près. Les quantités réelles conservées ne sont à valeurs uniques que lorsqu'un matrice unitaire de symétrie fait partie d'une famille arbitrairement proche de l'identité, et la condition de conservation devient alors une contrainte plus précise.
Les symétries peuvent être continument connectées à l'identité sont appelées continues, et les translations, rotations et accélérations en sont des exemples. Les symétries qui ne peuvent être continument connectés à l'identité sont discrètes, et l'opération d'inversion spatiale, de parité et de conjugaison de charge en sont des exemples.
L'interprétation des matrices comme générateurs de transformations canoniques est due à Paul Dirac. La correspondance entre symétries et matrices fut démontrée par Eugene Wigner comme étant complète, si les matrices antiunitaires décrivant les symétries incluant le renversement du temps sont incluses.
Règles de sélection
Il fut évident pour Heisenberg que, physiquement, les modules au carré des éléments de matrice de X, coefficients de Fourier de l'oscillation, correspondaient au taux d'émission de radiation électromagnétique.
Dans la limite classique des grandes orbites, si une charge de position X(t) et de valeur q oscille près d'une charge -q en position 0, de moment dipolaire instantané est qX(t), et la variation temporelle du moment se convertit directement en la variation spatiotemporelle du potentiel vectoriel, qui produit des ondes sphériques concentriques sortantes. Pour des atomes, la longueur d'onde de la lumière émise est d'environ 10 000 fois le rayon atomique, le moment dipolaire est la seule contribution au champ radiatif et les autres « détails » de la distribution atomique de charge peuvent être ignorés.
En ignorant la rétroaction, la puissance irradiée dans chaque mode sortant est une somme de contributions distinctes du module au carré de chaque mode de Fourier temporellement indépendant de d :
Et dans une représentation d'Heisenberg, les coefficients de Fourier du moment dipolaire sont les éléments de matrice de X. La correspondance permit à Heisenberg d'établir une loi pour les intensités de transition, la fraction du temps durant laquelle, à partir d'un état initial i, un photon est émis et l'atome « saute » vers l'état final j :
Cela permet l'interprétation statistique de l'intensité des éléments de matrice : elles donnent les intensités des raies spectrales, probabilité pour les sauts quantiques d'émission de la radiation dipolaire. Les taux de transition étant données par les éléments de matrice de X, tout élément Xij nul devrait impliquer une absence de transition. Ceci est appelé règle de sélection, et étaient très floues avant l'énoncé de la mécanique matricielle.
Un état arbitraire de l'atome d'hydrogène, sans prise en compte du spin, est symbolisé par |n;l,m>, où la valeur l est une mesure du moment angulaire orbital total et m est sont composant en z, qui définit l'orientation de l'orbitale.
Les composantes du pseudovecteur du moment angulaire sont :
et les produits dans cette expression sont indépendants de l'ordre et réels, car les différentes composantes de x et p commutent.
Les relations de commutation de L avec x (ou avec tout vecteur) sont simples à établir :
Cela vérifie que L génère des rotations entre les composantes du vecteur X.
À partir de là, le commutateur de Lz et des matrices de coordonnées x, y et z, peut être déduit :
ce qui signifie que les quantités x+iy et x-iy ont une règle de commutation simple :
Comme pour les éléments de matrice de x+ip et x-ip pour le hamiltonien de l'oscillateur harmonique, cette loi de commutation indique que ces opérateurs possèdent seulement quelques éléments non-diagonaux dans les états pour un m défini :
signifiant que la matrice (x+iy) transforme un vecteur propre de Lz de valeur propre m en un vecteur propre de valeur m+1. De même, (x-iy) soustrait une unité à m, et z ne change pas sa valeur. L'équation du mouvement d'Heisenberg définit les éléments de matrice de p dans la base d'Heisenberg à partir des éléments de matrice de x. qui convertit la partie diagonale de la relation de commutation en une règle de sommation de l'intensité des éléments de matrice : Cela donne une relation pour la somme des intensités spectroscopiques depuis et vers tout état donné, bien que pour être exacte dans l'absolu, les contributions de la probabilité de capture radiative pour les états diffusifs non liés doit être incluse dans la somme :
Donc dans une base d'états |l,m> où L2 et Lz ont des valeurs définies, les éléments de matrice de chacune des composantes de la position sont nuls sauf lorsque m est le même ou à une unité près.
Cela contraint la modification sur le moment angulaire total. N'importe quel état peut subir une rotation afin que son moment angulaire soit dans la direction z autant que possible, où m = l. L'élément de matrice sur la position agissant sur |l,m> peut seulement produire des valeurs de m plus élevées d'une unité, donc si les coordonnées subissent une rotation telle que l'état final soit |l',l'>, la valeur de l' peut être d'au mieux +1 par rapport à la plus grande valeur de l qui existe pour l'état initial. Donc l' est d'au plus l+1. Les éléments de matrice disparaissent pour l'>l+1, et un élément de matrice inverse étant déterminé par l'hermiticité, ils disparaissent aussi pour l' Lois de sommation
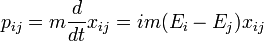
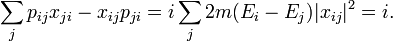
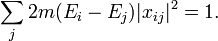
![[a,bc] = abc - bca = abc - bac + bac - bca = [a,b]c + b[a,c] \,](https://static.techno-science.net/illustration/Definitions/autres/4/43e6175512162f92356df19ec5de433a_568746c7d26bcbfba71fbddb73c16093.png)
![[p,x^n] = - i nx^{n-1} \,](https://static.techno-science.net/illustration/Definitions/autres/f/fedd9c8cefa9974d7a59fd5ed97cd89e_bf3862f92b7f0d65d0584377a834bb55.png)
![[p,f(x)] = -i f'(x) \,](https://static.techno-science.net/illustration/Definitions/autres/8/85e7bd813728a160352eb0a5fcb6707b_4ece98f086d051dd7b98b541ce003e8d.png)
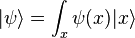

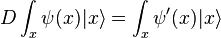
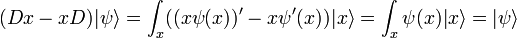
![[p+iD,x]=0 \,](https://static.techno-science.net/illustration/Definitions/autres/e/e9c5a8b285b5ce92559580119284bbd9_de86a0e4020918f4420dab4c1102b9dd.png)
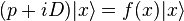
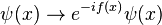
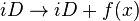
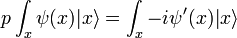
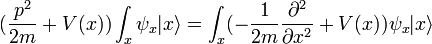
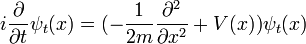
![[X_i ,X_j ] = 0 \,](https://static.techno-science.net/illustration/Definitions/autres/c/c997c0ef429f188116ba7530210216ed_42ccdef4a3537fae108966a7be732a08.png)
![[P_i, P_j ] = 0 \,](https://static.techno-science.net/illustration/Definitions/autres/9/9af252f18058e4301195f5e4fc723000_c6c34634911fdbbf9c7ec1d8d50b2836.png)
![[X_i ,P_j ] = i\delta_{ij} \,](https://static.techno-science.net/illustration/Definitions/autres/2/2e84611ca6fd82aeb0e3b091c166ca53_cbfbb932307b3d271a2d8b9917cf0c6c.png)
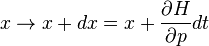
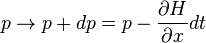
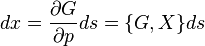
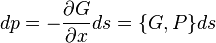
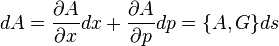
![dA = i [G,A] ds \,](https://static.techno-science.net/illustration/Definitions/autres/8/8283e1ec368b4887c06c4cbc7f8bc902_6e748d603fec03ab8263ad8c1c398789.png)
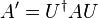
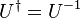
![dX = i[X,P] ds = ds \,](https://static.techno-science.net/illustration/Definitions/autres/1/1525eb83c22a5cc5df8ff48a4a60675a_512caea26803acb1a4b3f50bc2854584.png)
![dP = i[P,P] ds = 0 \,](https://static.techno-science.net/illustration/Definitions/autres/7/7053d93dd3e538ed940aa05513a444ff_1f035a2ffc9ad775dc8bb16f813cf5f3.png)
![{dH\over ds} = i[L,H] = 0 \,](https://static.techno-science.net/illustration/Definitions/autres/3/35516cd820df762eb9fe379eca9a8037_3b0c079f591c918f9ecccec7bfd744ab.png)
![{dL\over dt} = i[H,L] = 0 \,](https://static.techno-science.net/illustration/Definitions/autres/4/49fa4692bc31b01e3de049fccd585e1c_633b0352d6b25d4f8b3be4db0fcffd23.png)
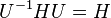
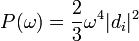
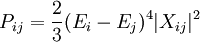
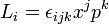
![[L_i, x_j] = i\epsilon_{ijk} x_k \,](https://static.techno-science.net/illustration/Definitions/autres/7/7f64e89ec5bbdd7b8db29a1439bf2da6_c12e504a2af9a04547ba42769ae0340f.png)
![[L_z , x] = iy \,](https://static.techno-science.net/illustration/Definitions/autres/a/a4a53f0a6318bfc6a1c72b02064a27af_67f8757e3a57be2bdfde204b91f18b5a.png)
![[L_z,y] = -ix \,](https://static.techno-science.net/illustration/Definitions/autres/d/d85f2aa2dd79c93576a4aea72769c622_96facf394eb295578425b4a0b5b2f28e.png)
![[L_z,x+iy] = (x+iy) \,](https://static.techno-science.net/illustration/Definitions/autres/1/1d5d05cf9a0b0dc9508393a4f650bba1_74181ceabf0b8bb7f64da1646d48fa3d.png)
![[L_z,x-iy] = -(x-iy) \,](https://static.techno-science.net/illustration/Definitions/autres/6/6670635e056b94c65ebbbd7da15598da_dd316486af3d49d27fe002bb3740d70f.png)