Mécanique matricielle - Définition
La liste des auteurs de cet article est disponible ici.
Développement mathématique
Une fois qu'Heisenberg eut introduit les matrices pour X et P, il put indiquer les éléments de matrice dans des cas spéciaux par intuition, guidé par le principe de correspondance. Les coefficients de matrice sont les analogues en mécanique quantique des coefficients de Fourier des orbites classiques, le cas le plus simple étant l'oscillateur harmonique, dans lequel X(t) et P(t) sont sinusoïdales.
Oscillateur harmonique
Dans les unités dans lesquelles masse et fréquence de l'oscillateur sont égales à un, l'énergie de l'oscillateur est :
Les lignes de niveau de H sont les orbites, des cercles concentriques. L'orbite classique d'énergie E est :
La vieille condition quantique indique que l'intégrale de P selon X sur une orbite, qui est l'aire de la surface du cercle dans l'espace des phases, doit être un multiple entier de la constante de Planck. L'aire du disque de rayon
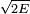
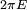
ou, en unités de longueur où

Les coefficients de Fourier de X(t) et P(t) sont très simples, surtout si elles sont combinés dans les quantités :
les deux quantités

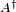
A(t) étant une série de Fourier classique avec seulement la plus basse fréquence, et l'élément de matrice Amn étant le (m-n)e coefficient de Fourier de l'orbite classique, la matrice de

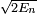
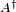

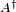
qui, au choix des unités près, sont les matrices d'Heisenberg pour l'oscillateur harmonique. Notons que les deux matrices sont hermitiennes, étant construites à partir des coefficients de Fourier de quantités réelles. Obtenir X(t) et P(t) est simple, en utilisant les coefficients de Fourier quantiques avec une évolution simple avec le temps.
Le produit matriciel de X et P n'est pas hermitien, mais possède une partie réelle et une partie imaginaire. La partie réelle est une moitié de l'expression symétrique (XP + PX), alors que la partie imaginaire est proportionnelle au commutateur [X,P] = (XP − PX). Il est facile de vérifier de manière explicite que (XP − PX) dans le cas de l'oscillateur harmonique est i, multiplié par l'identité.
est une matrice diagonale, avec pour valeurs propres Ei.
Conservation de l'énergie
L'oscillateur harmonique est très spécifique. Il est relativement simple d'écrire les matrices de manière exact, mais très difficile de découvrir les conditions générales pour ces formes spécifiques. Pour cette raison, Heisenberg a étudié l'oscillateur anharmonique, avec l'hamiltonien :
Dans ce cas, les matrices X et P ne sont plus des matrices hors diagonales, les orbites classiques correspondantes sont légèrement écrasées et déplacées, et possède des coefficients de Fourier à chaque fréquence classique. Afin de déterminer les éléments de matrices, Heisenberg postula que les équations classiques du mouvement peuvent être considérées comme des équations matricielles :
Il remarqua que si cela pouvait se faire, alors H considéré comme une fonction matricielle de X et P, auront une dérivée temporelle nulle.
où A * B est un produit symétrique.
-
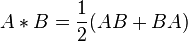
Une matrice constant est la même en tant que matrice diagonale, car tous les éléments non diagonaux ont une fréquence non nulle, ce qui indique aussi que H est diagonale.
Il est clair pour Heisenberg que dans ce système, l'énergie pouvait être conservée de manière exacte dans un système quantique classique, signe très encourageant pour les développements ultérieurs.
Problème de la dissociation - relations de commutations canoniques
Imposer la préservation des équations du mouvement ne constitue pas une condition suffisante pour déterminer les éléments de matrice. La constante de Planck n'apparait pas dans les équations classiques, ce qui implique que les matrices pourraient être construites pour de nombreuses valeurs différentes de

Afin de pouvoir continuer son raisonnement, Heisenberg avait besoin d'utiliser l'ancienne condition quantique afin de fixer les niveaux d'énergie, puis de remplir les matrices par les coefficients de Fourier des équations classiques, et enfin de modifier légèrement ces coefficients de matrices et les niveaux d'énergie afin d'assurer la satisfaction aux équations classiques. Cela n'était pas satisfaisant à l'évidence. Les anciennes conditions quantiques font références à l'aire définie par les orbites fines classiques, qui n'existaient plus dans le nouveau formalisme.
La plus importante découverte d'Heisenberg est comment transformer l'ancienne condition quantique en simple postulat de la mécanique matricielle. Afin de procéder à cette transformation, il étudia l'intégrale d'action comme une matrice quantité :
Il existe plusieurs problèmes avec cette intégrale, provenant tous de l'incompatibilité du formalisme matriciel avec l'ancienne description en termes d'orbites. Quelle est la période T à considérer ? De manière semi-classique, cela devrait être m ou n, mais la différence est d'ordre h et l'on veut une réponse à cet ordre. La condition quantique indique que Jmn est égal à 2πn sur la diagonale, donc le fait que J soit une constante de manière classique indique que les éléments non-diagonaux sont nuls.
Le progrès crucial fut de dériver la condition quantique par rapport à n. Cette idée ne prend son sens complet que dans la limite classique, où n n'est pas un entier mais la variable d'action J, mais Heisenberg fit des manipulations analogues avec les matrices, où les expressions intermédiaires sont parfois des différences discrètes et parfois des dérivées. Dans la discussion suivante, pour des raisons de clareté, la dérivation sera effectuée sur les variables classiques, puis la transition vers la mécanique matricielle sera faite grâce au principe de correspondance.
Dans le formalisme classique, la dérivée est la dérivée en fonction de J de l'intégrale qui définit J, donc égale à 1 de manière tautologique.
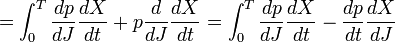
dans laquelle les dérivées dp/dJ dx/dJ devraient être interprétées comme des différences selon J sur des temps correspondants sur des orbites voisines, exactement ce qui serait obtenu en dérivant les coefficients de Fourier du mouvement orbital. Ces dérivées sont symplectiquement orthogonales dans l'espace des phases aux dérivées temporelles dP/dt dX/dt. L'expression finale est clarifiée par l'introduction de la variable conjuguée canoniquement à J, appelée variable d'angle θ. La dérivée en fonction du temps est une dérivée en fonction de

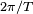
Ainsi l'intégrale de la condition quantique est la valeur moyenne sur un cycle du crochet de Poisson de X et P. Une différentiation analogue des séries de Fourier de PdX démontre que les éléments non-diagonaux du crochet de Poisson sont tous nuls. Le crochet de Poisson de deux variables conjuguées canoniquement comme X et P est la constante 1, donc l'intégrale est en réalité est la valeur moyenne de 1, donc 1, ce que l'on savait depuis le début (dJ/dJ=1). Mais Heisenberg, Born et Jordan n'étaient pas familiers avec la théorie des crochets de Poisson, donc ils durent faire la dérivation {X,P} in coordonnées J θ.
Le crochet de Poisson, contrairement à l'intégrale d'action, permet une translation simple vers la mécanique matricielle - à partir de la partie imagninaire du produit de deux variables, le commutateur. Afin de le constater, on peut considérer le produit de deux matrices A et B dans la limite de correspondance, dans laquelle les éléments de matrice sont des fonctions de l'index variant doucement, en gardant à l'esprit que la réponse est classiquement zéro.
Dans la limite de correspondance, lorsque les indices m n sont grands et proches, lorsque k, r sont petits, le taux de modification des éléments de matrice dans la direction diagonale est l'élément de matrice de la dérivée de J de la quantité classique correspondante. On peut alors déplacer tout élément de matrice diagonalement en utilisant la formule :
où le membre de droite est le seul (m-n)e coefficient de Fourier de (dA/dJ) sur une orbite proche de m à cet ordre semi-classique, qui n'est pas une matrice complètement et bien définie.
La dérivée temporelle semi-classique d'un élément de matrice est obtenu à un facteur i près en multipliant par la distance à la diagonale,
le coefficient Am(m + k) étant classiquement le ke coefficient de Fourier de la me orbite classique.
La partie imaginaire du produit de A et B peut être évalué en déplaçant les éléments de matrice de façon à reproduire la réponse classique, qui est nulle. Le résidu non nul qui résulte est alors donné intégralement par le déplacement. Tous les éléments de matrice étant à des indices ayant une distance faible à la position de grand indice (m,m), cela permet l'introduction de deux notations temporaires : A[r,k] = A(m + r)(m + k), pour les matrices, et (dA / dJ)[r] pour les re coefficients de Fourier des quantités classiques.
En changeant la variable de sommation dans la première somme r par r'=k-r, l'élément de matrice devient :
et il clair que la partie principale s'annule. La partie quantique qui vient est, en négligeant le produit des dérivées d'ordre élevé :
ce qui peut être identifié à i fois le ke coefficient de Fourier classique du crochet de Poisson. L'astuce originelle de la dérivation d'Heisenberg fut étendue à une dérivation complète semi-classique de la condition quantique en collaboration avec Born et Jordan.
Ils purent alors montrer que :
cette condition remplaça et étendit l'ancienne règle de quantification, permettant aux éléments de matrice de P et X pour un système arbitraire d'être déterminés simplement à partir de la forme du hamiltonien. La nouvelle règle de quantification fut postulée comme universellement vérifiée, même si sa déduction à partir de l'ancienne théorie quantique requérait un raisonnement semi-classique.
Vecteur d'état - mécanique quantique moderne
Afin de faire la transition vers la mécanique quantique moderne, le plus important ajout qui s'ensuivit fut le vecteur d'état quantique, écrit
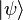
L'interprétation du vecteur d'état, dont les composantes sont écrites ψm, fut donnée par Born. Cette interprétation est statistique : le résultat de la mesure d'une quantité physique correspondant à la matrice A est aléatoire, avec une valeur moyenne égale à :
De manière alternative et équivalente, le vecteur d'état donne la amplitude de probabilité ψi pour le système quantique d'occuper l'état d'énergie i. Une fois le vecteur d'état introduit, la mécanique matricielle pouvait être adaptée à toute base, dans laquelle la matrice H n'est pas forcément diagonale. L'équation du mouvement d'Heisenberg dans sa forme originelle indique que Amn évolue dans le temps comme un coefficient de Fourier :
qui peut être écrit sous la forme différentielle :
et il peut être réécrit de façon à être vérifié dans une base arbitraire en notant que la matrice H est diagonale avec pour coefficients diagonaux Em :
Cela devient alors une équation matricielle, valable pour toute base. C'est la forme moderne de l'équation du mouvement d'Heisenberg. La solution formelle est :
Toutes les formes de l'équation du mouvement ci-dessus signifient la même chose, que A(t) est égal à A(0) à une rotation de base près par la matrice unitaire eiHt. Par rotation de la base pour le vecteur d'état à chaque instant par eiHt, on peut lever la dépendance temporelle dans les matrices. Les matrices sont maintenant indépendantes en temps, mais le vecteur d'état subit une rotation :
Il s'agit de l'équation de Schrödinger pour le vecteur d'état, et la transformation dépendante en temps de la base est sa transformation en représentation de Schrödinger.
En mécanique quantique, dans la représentation de Heisenberg, le vecteur d'état
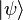
Le terme supplémentaire est pour des opérateurs comme A = (X + t2P) qui présentent une dépendance temporelle explicite en plus de la dépendance temporelle pour l'évolution unitaire. La représentation de Heisenberg ne distingue pas le temps de l'espace, ce qui est particulièrement intéressant pour les théories relativistes.
De plus, la similitude à la physique classique est plus apparente : les équations hamiltoniennes du mouvement pour la mécanique classique sont reconstituées en remplaçant le commutateur ci-dessus par le crochet de Poisson.
Selon le théorème de Stone-von Neumann, les représentations d'Heisenberg et de Schrödinger sont unitairement équivalentes.
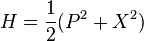
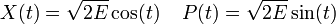
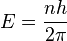
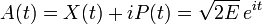
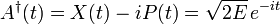
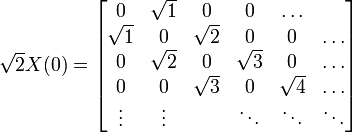
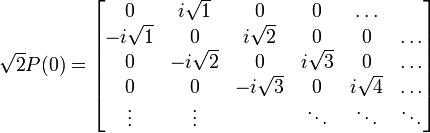
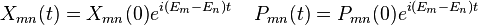
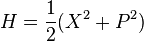
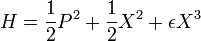
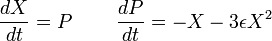
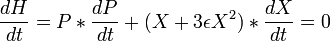
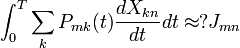
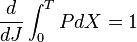
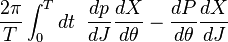
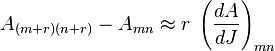
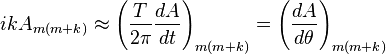
![(AB - BA)(0,k) = \sum_{r=-\infty}^{\infty} ( A[0,r] B[r,k] - A[r,k] B[0,r] )](https://static.techno-science.net/illustration/Definitions/autres/b/b0a7fe2b4da131be388950af49cc92fa_a3c0fa9a00027227b017cf460fcd3b58.png)
![= \sum_r (\; A[-r+k,k] + (r-k){dA \over dJ}[r]\; ) (\; B[0,k-r] + r {dB\over dJ}[r-k] \; ) - \sum_r A(r,k)B(0,r) \,](https://static.techno-science.net/illustration/Definitions/autres/e/e1b3f462482aed425076adf260f8ae97_6b91ca30038284a276bb645b8bf3ac36.png)
![\sum_{r'} (\;A[r',k] - r' {dA \over dJ}[k-r']\;)(\; B[0,r'] +(k-r'){dB\over dJ}[r']\;)- \sum_r A[r,k] B[0,r] \,](https://static.techno-science.net/illustration/Definitions/autres/5/51dd5353a19148f34389ab11e8623e35_1a4f9d0a0eed54ed000b2d7bdd21cbcb.png)
A[r',k] - {dA\over dJ}[k-r'] r' B[0,r'])](https://static.techno-science.net/illustration/Definitions/autres/a/a77f0feccd2fa33e04e634aa6c4917b6_77fe5a37259b7c50d5495284617a60a5.png)
![\sum_{r'} (\; {dB\over dJ}[r']i{dA\over d\theta}[k-r'] - {dA\over dJ}[k-r']i{dB\over d\theta}[r']) \,](https://static.techno-science.net/illustration/Definitions/autres/8/8b3d3b861fce0a6fb8c41178226868ed_3ac0b82a2dacdf51bc0e262b339f36e8.png)
![[ X , P ] = XP - PX = i \{X,P\}_\mathrm{PB} = i \,](https://static.techno-science.net/illustration/Definitions/autres/1/1666e3175673c45493b631c7d49ce029_4dad6fb9b354b71f0a7dc010a9290f53.png)
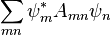
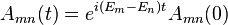
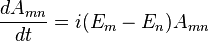
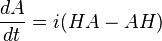
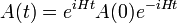
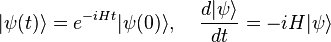
![\frac{dA}{dt} = {i \over \hbar } [ H , A(t) ] + \frac{\partial A}{\partial t}](https://static.techno-science.net/illustration/Definitions/autres/b/b8485db33c78a6b948886ed1fd437706_1aad7b14277a9df130deb8a41aa80948.png)

















































