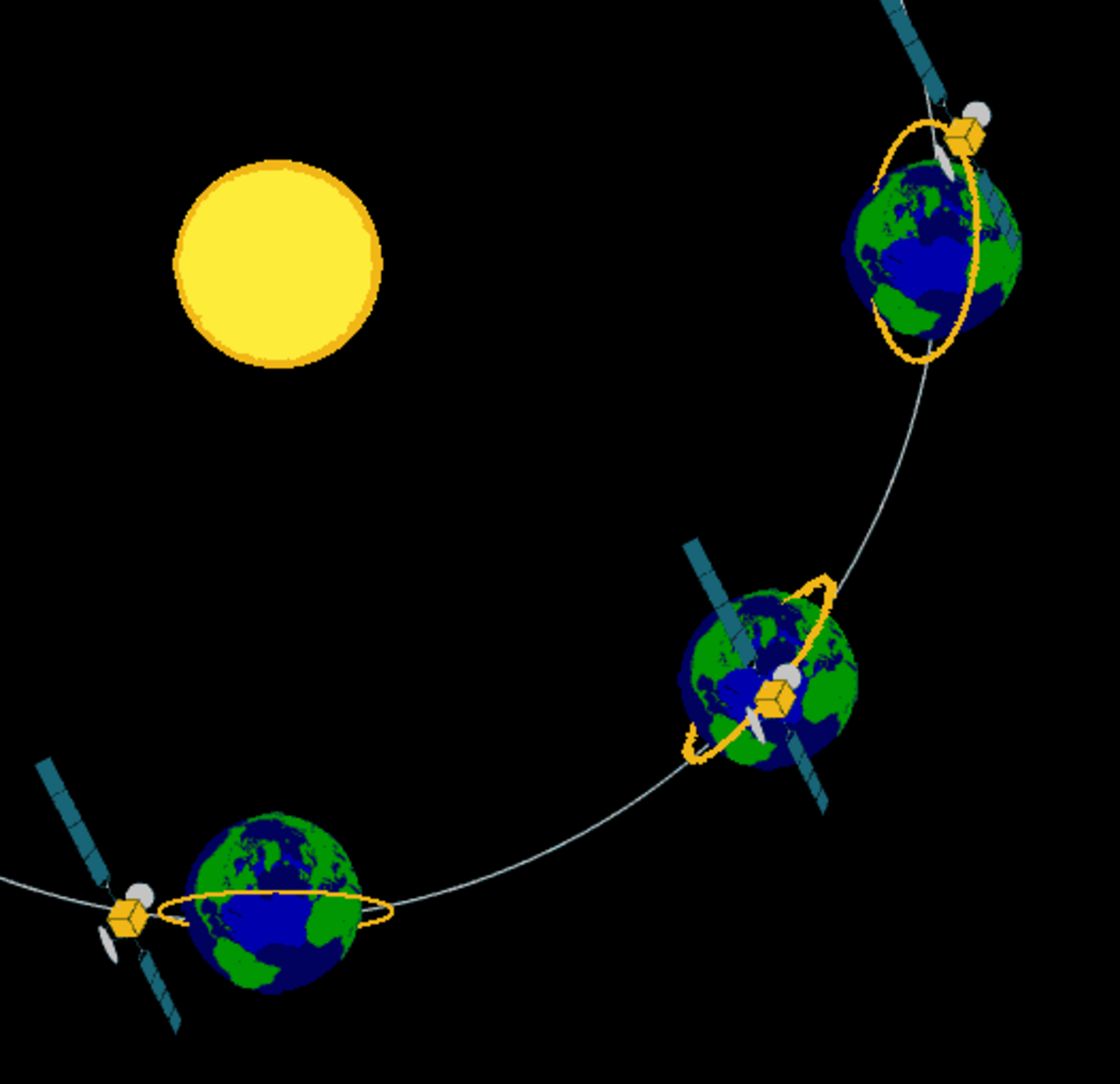
Orbite héliosynchrone - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe - Éléments techniques - Techniques - Historique

Introduction

Le plan d'orbite d'un satellite artificiel héliosynchrone se présente toute l'année sous le même angle par rapport au soleil.

Un satellite héliosynchrone repasse quotidiennement au-dessus d'un lieu à une heure solaire identique.

Étymologiquement et par analogie avec l'orbite géosynchrone, une orbite héliosynchrone (du grec ancien Ἥλιος, èlios, personnification du soleil) est une orbite héliocentrique (autour du Soleil) de rayon ~24,360 Gm (0,1628 ua) telle que la période de révolution de l'objet coïncide avec la période de rotation du Soleil. L'orbite héliostationnaire est l'orbite héliosynchrone d'inclinaison et d'excentricité orbitale zéro.

Pour un satellite artificiel, l'orbite héliosynchrone désigne une orbite géocentrique (autour de la Terre) dont on choisit l'altitude et l'inclinaison de façon à ce que l'angle entre le plan d'orbite et la direction du soleil demeure à peu près constant. Un satellite placé sur une telle orbite repasse au-dessus d'un point donné de la surface terrestre à la même heure solaire locale. Cette orbite est utilisée par tous les satellites qui effectuent des observations photographiques en lumière visible, car l'éclairement solaire du lieu observé sera peu variable d'un cliché à l'autre : satellites météorologiques, satellite de reconnaissance, satellite de télédétection, etc.. Il s'agit d'une orbite polaire (qui passe près du pôle), basse (entre 600 et 1000 km) et de périodicité courte (décrite toutes les 96 à 110 minutes). Le satellite coupe environ 12 fois par jours le plan de l'équateur terrestre et survole les lieux vers 15h locale.

Principe

L'usage le plus répandu de l'expression orbite héliosynchrone concerne surtout une orbite géocentrique dont on choisit l'altitude et l'inclinaison de façon à ce que l'angle entre le plan d'orbite et la direction du soleil demeure à peu près constant, en dépit de la dérive du nœud ascendant de l'orbite qui se traduit par la précession du plan de cette orbite. Cette dérive est due à l'influence du bourrelet équatorial de la Terre. Elle dépend de l'inclinaison, du grand axe et de l'excentricité de l'orbite. Un satellite placé sur une telle orbite repasse au-dessus d'un point donné de la surface terrestre à la même heure solaire locale. Il y aura une oscillation annuelle de l'heure solaire du passage à cause de l'excentricité orbitale terrestre (voir analemme).

Éléments techniques

Pour une orbite directe, la précession est rétrograde, c'est-à-dire, en sens opposé à celui de la rotation terrestre ; aussi les orbites héliosynchrones sont-elles rétrogrades, assurant une précession directe. Une bonne approximation du taux de précession pour le cas particulier d'une orbite circulaire (excentricité nulle) est donnée par :

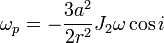
$\omega_p = -\frac{3 a^2}{2 r^2} J_2 \omega \cos i$

Où $ω p$ est le taux de précession du nœud ascendant en (rad/s), $a$ est le rayon équatorial terrestre (6,378 137 Mm), $r$ est le rayon orbital du satellite, $ω$ sa fréquence angulaire ( $2π$ radians divisé par sa période), $i$ son inclinaison et $J 2$ est le second facteur de forme dynamique terrestre (1,08×10⁻³). Cette dernière quantité est liée à l'aplatissement comme suit :

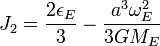
$J_2 = \frac{2 \epsilon_E}{3} - \frac{a^3 \omega_E^2}{3 G M_E}$

Où $ε E$ est l'aplatissement terrestre, $ω E$ le taux de rotation terrestre (7,292 115×10⁻⁵ rad/s), et $G M E$ est le produit de la constante gravitationnelle universelle et de la masse terrestre (3,986 004 418×10¹⁴ m³/s²).