Particule virtuelle - Définition

Particules virtuelles et interactions

En dehors des fluctuations du vide, les particules virtuelles se retrouvent aussi dans les processus plus concrets d'interaction entre particules. Nous avons vu que des particules pouvaient être créées ou détruites lors de collisions entre particules. Par conséquent, des particules peuvent très bien exister un bref instant, le temps d'une interaction.

Lorsque l'on a essayé de trouver une formulation relativiste de l'équation de Schrödinger, on est rapidement tombé sur des difficultés. Ainsi l'équation de Dirac autorise pour les électrons autour d'un atome, aussi bien des états d'énergie négative que positive. Cela est une conséquence du fait que l'équation de Dirac respecte la relation relativiste E² = p²c² + m²c⁴ où le signe de l'énergie n'est pas défini.

Comment interpréter ces états d'énergie négative ? On pourrait imaginer que c'est un artefact théorique. En relativité classique aussi on peut très bien avoir des états d'énergie négative, pour la même raison. Mais ces états sont totalement découplés des états d'énergie positive et ils peuvent être ignorés. Malheureusement, ici, ce n'est pas le cas. Les états d'énergie positive et négative sont couplés. Et si l'on part d'un atome avec un électron ayant une énergie positive, le calcul montre qu'au court du temps on aboutit aussi à des états d'énergie négative.

Plus grave, comme il est possible d'extraire une quantité arbitraire d'énergie d'un électron, les atomes ne sont plus stables. L'électron peut descendre sur des niveaux d'énergie de plus en plus négatif (après avoir passé le "gap" égal à 2mc² où m est la masse de l'électron) en émettant indéfiniment des photons. Ce qui ne correspond évidemment pas à l'observation.

La solution de Dirac fut d'imaginer que tous les états d'énergie négative étaient occupés (la mer de Dirac) et d'invoquer le principe d'exclusion de Pauli pour expliquer que les électrons "observables" ne tombent pas dans des états d'énergie négative. De plus, si on excite un électron de la mer de Dirac cela laisse un "trou" qui se comporte exactement comme un électron de charge positive, un positron. Ce fut la première prédiction de l'existence de l'antimatière.

Toutefois cette théorie n'est pas entièrement satisfaisante car elle ne marche que pour les fermions. La bonne approche consiste à changer carrément son fusil d'épaule et à s'attaquer directement à une formulation de la théorie autorisant un nombre variable de particules (ce qui est d'ailleurs naturel dans un contexte relativiste) et à réinterpréter les états d'énergie négative comme des états d'énergie positive de particules d'antimatière (voir la théorie des champs).

On est alors conduit naturellement à décrire l'interaction des particules comme résultant de l'échange de particules virtuelles sous forme d'un diagramme de Feynman. Un processus d'interaction donné s'obtenant par la "somme" de tous les diagrammes autorisés par les lois de conservation.

Un exemple typique est l'interaction de deux électrons par l'échange d'un photon virtuel :

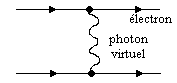
Particules virtuelles et forces à distance

Une application intuitive, simple et intéressante des particules virtuelles est leur utilisation dans les forces à distance.

Nous avons dit que l'interaction de deux particules (comme dans le premier diagramme ci-dessus) était modélisée par l'échange de particules virtuelles. Nous pouvons donc considérer que l'interaction de deux particules distantes (interaction électrostatique, interaction nucléaire) se fait par l'échange d'une particule virtuelle "médiateur" de cette interaction. Ces particules sont aussi appelées bosons de jauge car elles sont une conséquence de la description des interactions dans le formalisme des théories des champs de jauge.

Les médiateurs des interactions sont les suivants :

• Interaction gravitationnelle : graviton (hypothétique).
• Interaction électromagnétique : photon.
• Interaction faible : boson Z et boson W.
• Interaction forte : gluon.
• Interaction nucléaire : méson pi. Cette dernière étant une conséquence de l'interaction forte.

Imaginons par exemple deux électrons situés à une certaine distance L l'un de l'autre.

Ces deux électrons vont échanger des photons virtuels. Cet échange va provoquer une variation de l'énergie globale du couple d'électrons et se traduire par une force d'interaction électrostatique.

Voyons cela de manière plus quantitative.

Avertissement : ce calcul est intuitif et ne sert qu'à illustrer l'idée. Un calcul plus précis doit faire appel à l'arsenal de la théorie quantique des champs et on ne doit pas prendre le résultat présent comme un résultat théorique précis !

On peut concevoir que si les électrons échangent un photon d'énergie E, alors l'énergie globale du couple d'électrons va être modifiée d'une quantité environ proportionnelle à E. La constante k de proportionnalité dépendant du couplage entre électrons et photons.

Mais les photons virtuels doivent parcourir la distance L et ils ne peuvent le faire qu'à la vitesse de la lumière. C’est-à-dire en un temps égal à t = L / c.

Le principe d'incertitude nous dit alors que l'énergie des photons virtuels sera de l'ordre de . Bien entendu, c'est un ordre de grandeur car le principe d'incertitude dit bien ce qu'il est : une incertitude. Il faudrait faire un calcul plus précis. Par exemple, les calculs de la théorie quantique des champs montrent que l'énergie des fluctuations du vide suit une distribution de Poisson.

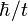
L'énergie d'interaction sera donc approximativement :

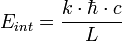
Et donc, pour avoir la force d'interaction, il faut dériver cette expression par la distance :

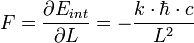
La force d'interaction électrostatique diminue donc comme le carré de la distance.

On peut comparer ce résultat à la force de Coulomb entre deux charges élémentaires : Dans ce cas, on trouve comme ordre de grandeur pour la constante de proportionnalité sans dimension k : k = 0.007

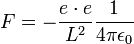
Petit résultat amusant et qui peut faire réfléchir : ce résultat ne dépend pas du nombre de dimensions spatiales. Alors, qu'en électromagnétisme classique, l'intensité de la force électrostatique diminue comme le carré de la distance car l'espace est à trois dimensions (l'intensité d'une onde électromagnétique sphérique diminue comme l'inverse de la surface de la sphère donc comme le carré de son rayon).

Qu'en est-il maintenant d'une interaction comme l'interaction nucléaire ?

Cette fois la particule est massive. Le méson pi est même nettement plus lourd que l'électron, par exemple. La distance que peut parcourir la particule n'est plus quelconque. En effet, l'énergie de la particule ne peut pas être inférieure à mc² où m est la masse de la particule. Par conséquent, son temps d'existence est au mieux de l'ordre de . Et comme la particule ne peut pas aller plus vite que la lumière, elle ne pourra parcourir qu'une courte distance.

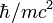
On prédit donc que pour un vecteur d'interaction massif, la force va rapidement décroître pour devenir quasiment inexistante au-delà d'une distance de l'ordre de :

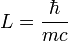
Par exemple, le boson Z a une masse d'environ 91 GeV (le boson W est plus léger mais il est chargé et ses échanges ne peuvent que se faire par paires ou par changement de charge des particules en interaction). Cela donne une distance de l'ordre de .