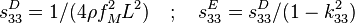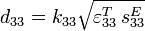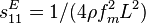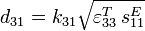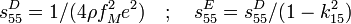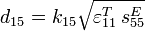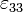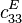Piézoélectricité - Définition
La liste des auteurs de cet article est disponible ici.
Méthodes de mesures et de caractérisation
De manière générale, on entend par caractérisation d'un matériau la détermination d'un certain nombre de ses paramètres permettant d'évaluer sa qualité et son adaptation à une application donnée. On caractérise un matériau piézoélectrique en mesurant notamment ses propriétés électromécaniques, ses coefficients de couplage électromécanique ou son facteur de qualité mécanique selon l'application visée.
Mesures d'impédance complexe
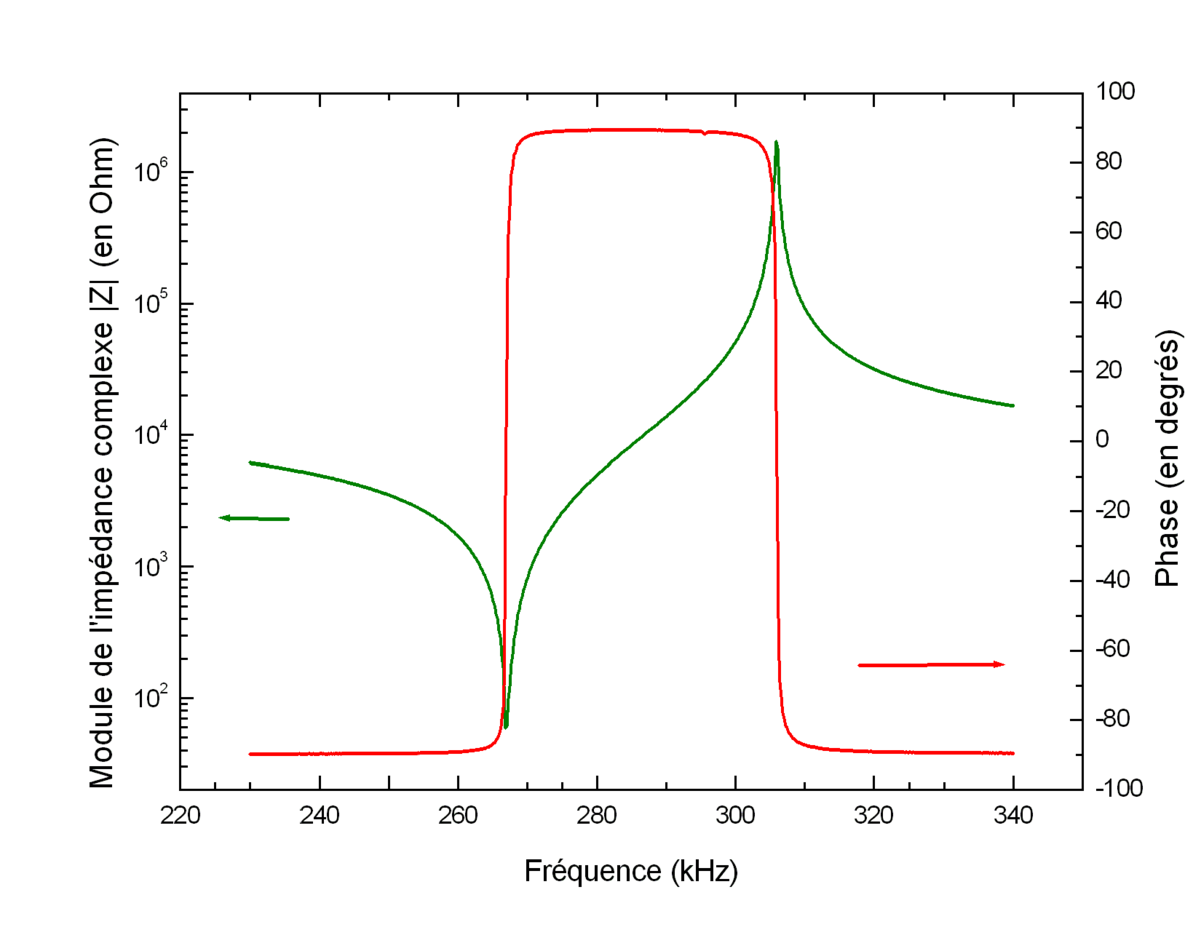
Cette méthode, parfois appelée Méthode IRE, est la méthode standard de caractérisation des céramiques piézoélectriques. En mesurant l'impédance complexe de différents échantillons de formes et de dimensions différentes en fonction de la fréquence, on remonte aux différentes caractéristiques du matériau : propriétés électromécaniques, coefficients de couplage, facteurs de qualités mécanique. La procédure est normalisée dans la norme de l'IEEE et décrite au moins partiellement dans les ouvrages de référence.
En pratique, on taille plusieurs échantillons de manière à isoler un mode propre de vibration particulier, c'est-à-dire à rejeter les autres modes propres à des fréquences beaucoup plus hautes ou beaucoup plus basses. Au voisinage de la fréquence de ce mode propre, le spectre d'impédance de l'échantillon présente un minimum et un maximum à des fréquences dites de résonance et d'anti-résonance. Ces deux fréquences permettent directement de calculer une constante élastique et un coefficient de couplage électromécanique. En mesurant indépendamment (en général à basses fréquences) la constante diélectrique des échantillons, on peut ensuite calculer un coefficient piézoélectrique. En effectuant cette opération pour plusieurs modes propres de vibration, on peut ainsi déterminer toutes les propriétés du matériau.
Le tableau suivant présente trois exemples de modes de vibrations utilisés pour la détermination de quelques coefficients de couplage, coefficients piézoélectriques et compliances élastiques d'une céramique ou d'un monocristal piézoélectrique. Dans ce tableau, fM et fm désignent les fréquences où l'impédance est maximale et minimale respectivement, L, e et ρ sont la longueur, l'épaisseur et la masse volumique de l'échantillon. La flèche donne la direction de polarisation de l'échantillon ; les électrodes sont représentées par les zones hachurées.
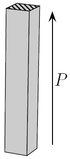
| Coeff. de couplage |
![k_{33}^2 = \frac{\pi}{2}\frac{f_m}{f_M}\tan\left[\frac{\pi}{2}\left(1-\frac{f_m}{f_M}\right)\right]](https://static.techno-science.net/illustration/Definitions/autres/3/3a12bb96cba66a476c46bf4417d16296_95d9b2224fa6e4367fcf81002f65e8df.png)
|
| Compliance élastique |
| |
| Coeff. piézoélectrique |
| |
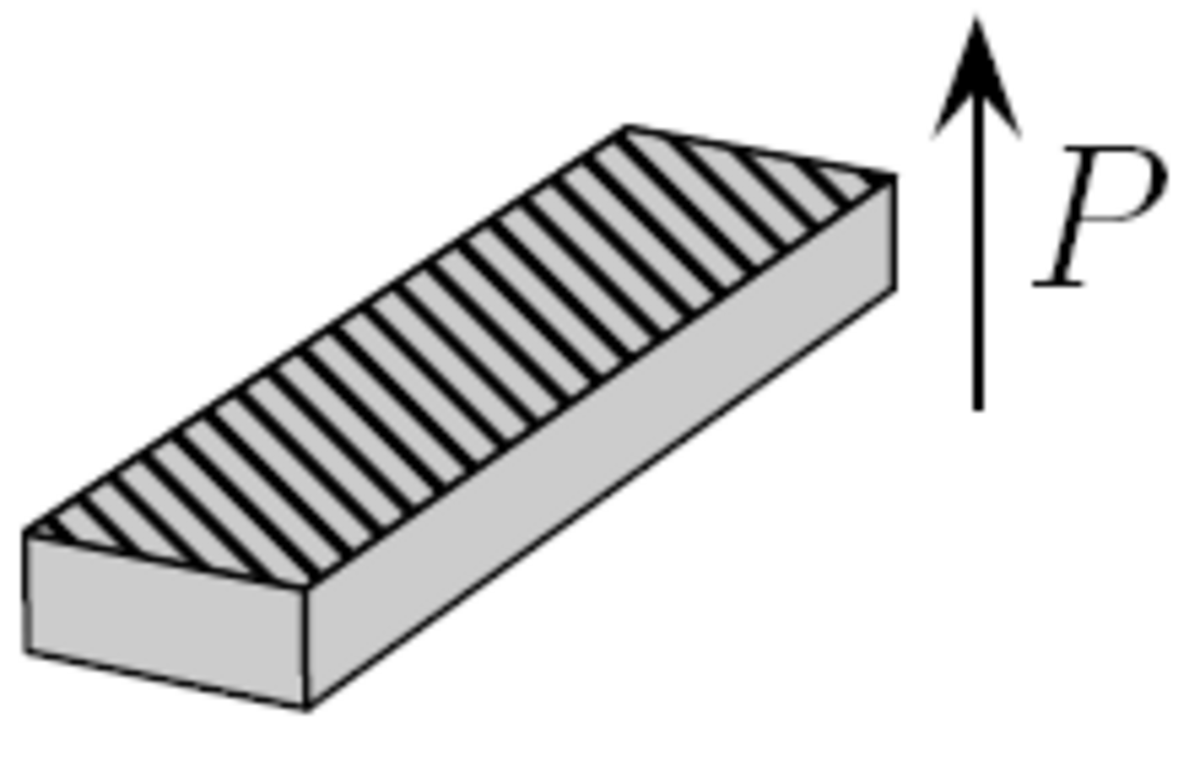
| Coeff. de couplage |
![\frac{k_{31}^2}{1-k_{31}^2} = \frac{\pi}{2}\frac{f_M}{f_m}\tan\left[\frac{\pi}{2}\left(\frac{f_M}{f_m}-1\right)\right]](https://static.techno-science.net/illustration/Definitions/autres/3/385f83a0dad27f008104d02c710cbfcf_6e144049b0258b0f6d533f96a27de230.png)
|
| Compliance élastique |
| |
| Coeff. piézoélectrique |
| |
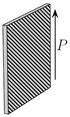
| Coeff. de couplage |
![k_{15}^2 = \frac{\pi}{2}\frac{f_m}{f_M}\tan\left[\frac{\pi}{2}\left(1-\frac{f_m}{f_M}\right)\right]](https://static.techno-science.net/illustration/Definitions/autres/3/31e812136c2f855b6c61c78b8b1a72bc_2a89b8788fcffe73db8a2899b4efc568.png)
|
| Compliance élastique |
| |
| Coeff. piézoélectrique |
|
Méthode de Berlincourt
La méthode de Berlincourt, nommée d'après le physicien Don Berlincourt, est une mesure de l'effet piézoélectrique direct. L'échantillon à mesurer est coincé entre deux pièces métalliques et soumis à une contrainte cyclique. Un condensateur est connecté en parallèle, de sorte que le courant produit par l'effet piézoélectrique vient charger le condensateur. Une mesure de la tension aux bornes du condensateur permet de calculer la charge totale et de remonter au coefficient piézoélectrique d33. L'amplitude de la contrainte appliquée est mesurée selon un principe analogue, à l'aide d'un élément piézoélectrique connu placé en série avec l'échantillon.
Cette méthode est rapide, facile à mettre en œuvre et relativement peu onéreuse. Contrairement à la méthode précédente, elle permet d'obtenir le signe du coefficient piézoélectrique d33. Divers appareils sont disponibles dans le commerce. Les modèles les plus élaborés permettent d'étudier les non-linéarités en faisant varier la fréquence ou l'amplitude de la contrainte appliquée.
Les limites de cette technique tiennent à la difficulté de produire dans l'échantillon une contrainte parfaitement homogène. La forme des contacts est importante : un contact en pointe aura tendance à créer des contraintes inhomogènes tandis qu'un contact plat tendra à créer des contraintes latérales à cause des effets de frictions et fera baisser la valeur mesurée.
Méthodes acoustiques
Il existe plusieurs méthodes acoustiques permettant de déterminer les caractéristiques d'un matériau piézoélectrique.
La méthode la plus utilisée consiste à émettre une impulsion sur une face d'un échantillon et de mesurer l'écho de l'onde ainsi créée. La mesure de la durée écoulée entre l'émission de l'onde et son écho permet de mesurer sa vitesse et de là de calculer les constantes élastiques « durcies ». Cette méthode, comme la suivante, nécessite une mesure indépendante des constantes diélectriques du matériau.
La spectroscopie de résonance acoustique consiste à remonter aux propriétés électromécaniques d'un matériau à partir des fréquences propres de vibration d'un objet. C'est une méthode utilisée couramment en mécanique. Son utilisation pour les matériaux piézoélectriques est plus délicate car le nombre de paramètres à déterminer est plus grand.
Autres méthodes
Il est également possible de mesurer la vitesses des ondes acoustiques par diffusion Brillouin. La diffusion Brillouin est la diffusion inélastique de la lumière par les ondes élastiques se propageant dans le cristal. Son utilisation pour la détermination des constantes élastiques est classique pour les matériaux non piézoélectriques. Elle peut être étendue au cas des piézoélectriques ; elle a été notamment utilisée pour la détermination des propriétés de certains piézoélectriques modèles (BaTiO3, PbTiO3, KNbO3) mais souffre de plusieurs limitations et n'est utilisée qu'à des fins de recherche.
L'interférométrie laser permet de mesurer directement un déplacement en fonction d'un champ électrique appliqué. Il est possible d'en déduire un coefficient piézoélectrique. C'est une méthode bien moins générale et moins complète que les méthodes précédentes, mais elle permet d'effectuer des mesures sur des dispositifs piézoélectriques intégrés comme les MEMS.
Propriétés de quelques matériaux types
Les coefficients rapportés dans le tableau suivant relient l'allongement d'une barre (sans unité) au champ électrique appliqué entre ses deux extrémités (en V/m). L'unité du système international pour ce coefficient est donc le mètre par volt (m/V). Les indices (33) se rapportent à la direction cristallographique correspondant à la longueur de la barre.
| Matériau | Coeff. piézo. d33 (10-12 m/V) | Permittivité relative | Module d'Young | Coeff. de couplage k33 (%) |
|---|---|---|---|---|
| Quartz | 2,3 | 4,5 | 80 | 10 |
| BaTiO3 (céramique) | 190 | 1700 | 106 | 52 |
| PbTiO3 | 120 | |||
| PZT (45/55) | 140 | 450 | 71 | 60 |
| PZN-9PT | 2500 | |||
| LiNbO3 | 6 | 30 | 2,45 | 17 |