Polytope régulier - Définition
La liste des auteurs de cet article est disponible ici.
Polytopes dans la nature
Échelle microscopique
Dans l'univers des minéraux, les cristaux présentent très souvent des faces triangulaires carrées ou hexagonales régulières. Les tétraèdre, cube et octaèdre se retrouvent dans les cristaux. C'est l'observation des cristaux qui a conduit les géomètres à s'intéresser aux pavages du plan et de l'espace. La classification des pavages réguliers du plan est aujourd'hui bien connue, elle comporte 17 pavages différents. Lire Structures cristallines.
Les quasi-cristaux peuvent posséder des pentagones réguliers. Le pavage de Penrose donne une idée de l'agencement des structures dans les quasi-cristaux : il s'agit d'un pavage non régulier du plan par pentagones, losanges et pentagrammes, présenté par Roger Penrose.
Au tout début du XXe siècle, Ernst Haeckel décrivit un nombre d'espèces de radiolaires, dont certains squelettes prennent des formes polyédrales. Les exemples incluent Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus et Circorrhegma dodecahedra ; évidemment, le nom reflète la forme.
Plus récemment ont été découvertes de nouvelles molécules de carbones, connues comme fullerènes.
Échelles humaines
Un autre exemple de polygones réguliers résultat d'un processus géologique peut être observé dans la Chaussée des Géants en Irlande ou dans le Devil's Postpile en Californie : des coulées de lave ont formé des zones d'empilement de colonnes hexagonales de basalte. L'explication de la régularité est une compensation symétrique de la somme des contraintes subies. L'exemple le plus célèbre de polygones dans le règne animal se trouve dans les construction en cire des abeilles ou en cellulose des guêpes. Les ruches présentent des pavages d'hexagones réguliers, utilisés pour stocker le pollen récolté et le miel, nourriture pour les larves (lire alvéole d'abeille).
Il existe des animaux présentant eux-mêmes des formes de polygones réguliers, ou du moins des formes possédant les mêmes symétries. L'étoile de mer a les mêmes symétries qu'un pentagone, parfois d'autres polygones réguliers, suivant les espèces. Les échinodermes ne présentent pas réellement une symétrie axiale parfaite. Les toiles d'araignée présentent des formes polygonales, avec une certaine régularité.
Les symétries radiales sont largement observées dans le règne végétal. En particulier : les fleurs, et dans une moindre mesure, les fruits et légumes. Par exemple, la carambole (un fruit tropical populaire en Asie), dans la section ressemble à un pentagone.
Échelles cosmologiques
Quittons la Terre, changeons d'échelle. Les galaxies spirales offrent des figures de pentagones.
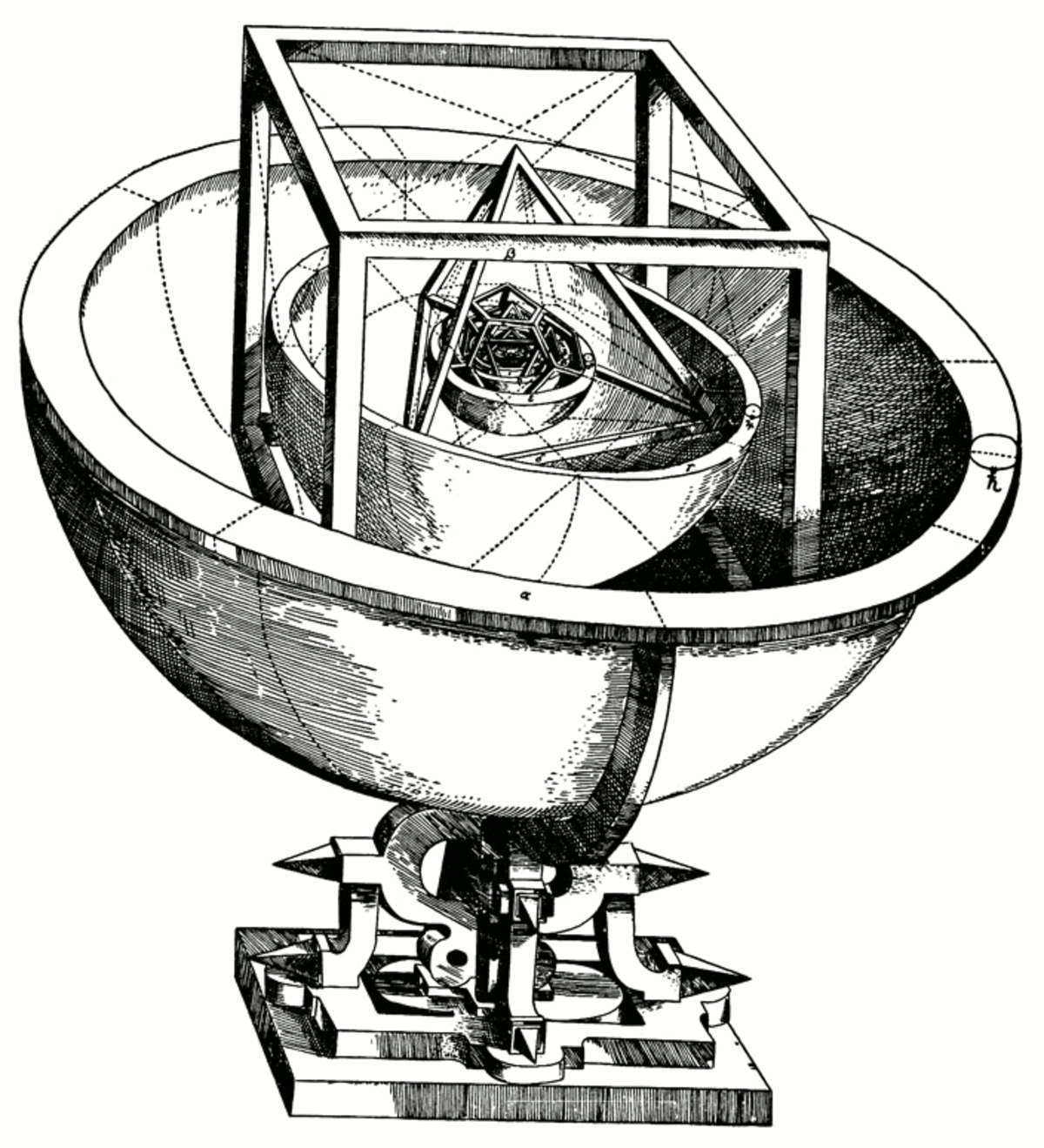
Les pythagoriciens pensaient à une harmonie entre les orbites des planètes du système solaire et les polyèdres réguliers. Au XVIIe siècle, Johannes Kepler étudia de près les observations astronomiques de Tycho Brahe. Pendant une décennie, il tenta en vain d'établir l'idéal pythagoricien, de faire un lien entre les tailles des polyèdres et la taille des orbites des planètes. Il échoua dans ses objectifs premiers, mais ses découvertes le conduisirent à formaliser ce qui est aujourd'hui appelé les trois lois de Kepler.