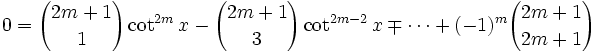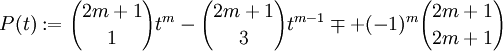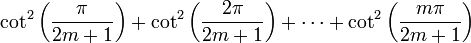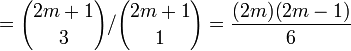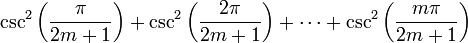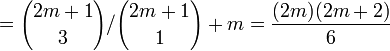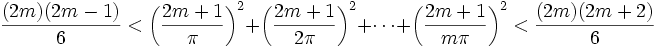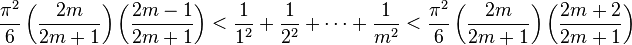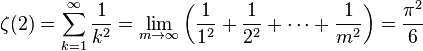Problème de Bâle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le problème de Bâle (connu parfois aussi sous le nom de « problème de Mengoli ») est un problème célèbre dans la théorie des nombres, posé en premier par Pietro Mengoli en 1644, et résolu par le mathématicien suisse Leonhard Euler en 1735, dont Bâle était la ville natale. Le problème résistait aux attaques des mathématiciens éminents de l'époque, ainsi, la solution d'Euler lui apporta une notoriété immédiate à l'âge de 28 ans. Il a considérablement généralisé le problème et ses idées furent reprises par le mathématicien allemand Bernhard Riemann dans son article de 1859, dans lequel il a défini sa fonction ζ et a démontré ses propriétés de base.
Le problème demande la valeur exacte de la somme de la série :
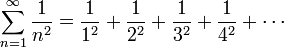
Celle-ci est approximativement égale à 1,64493406684822643. Vue la lente convergence de la série, une telle valeur approchée n'a pu être trouvée qu'en mettant en œuvre des méthodes d'accélération de convergence, ce qui est fait notamment par Stirling en 1730 et Euler en 1731. Euler trouva finalement la somme exacte
Il annonça cette découverte en 1735. Ses arguments étaient basés sur des manipulations qui ne furent pas justifiées, et ce n'est que dix ans plus tard qu'il fut capable de produire une démonstration rigoureuse.
Euler attaque le problème
La déduction d'Euler de la valeur π2 / 6 est intelligente et originale. Il développa essentiellement des observations sur les polynômes finis et assura que ces mêmes propriétés sont toujours vraies pour les séries infinies. Le raisonnement original d'Euler requiert une justification, mais même sans justification, en obtenant la valeur correcte, il fut capable de la vérifier numériquement par rapport aux sommes partielles de la série. La concordance qu'il observa lui inspira suffisamment confiance pour annoncer son résultat à la communauté mathématique.
Pour suivre l'argument d'Euler, rappelons le développement en série de Taylor de la fonction sinus
En divisant par
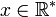
Maintenant, les racines de sin(x) / x apparaissent précisément pour
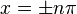
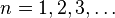
Si nous multiplions formellement ce produit et factorisons tous les termes
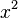
Mais, à partir du développement de la série infinie originale de sin(x) / x, le coefficient de x2 est
Ces deux coefficients doivent être égaux ; ainsi,
En multipliant les deux côtés de cette équation par − π2, nous obtenons la somme des inverses des carrés d'entiers positifs.
Une démonstration rigoureuse
L'argument suivant prouve l'identité ζ(2) = π2 / 6, où ζ(s) est la fonction zêta de Riemann. C'est de loin, la démonstration la plus simple disponible ; car la plupart des démonstrations utilisent des résultats de mathématiques avancées, telle que les séries de Fourier, l'analyse complexe, et le calcul à plusieurs variables ; celle qui suit ne requiert même pas le calcul à une variable (bien qu'une limite soit prise à la fin).
Historique de la démonstration
L'origine de cette démonstration n'est pas claire. Elle apparaît dans le journal Eureka en 1982, attribuée à John Scholes, mais Scholes déclara qu'il avait appris la démonstration de Peter Swinnerton-Dyer, et dans tous les cas il maintient que la démonstration était un « savoir commun de Cambridge à la fin des années 1960 ».
Ce que vous avez besoin de connaître
Pour comprendre la démonstration, vous aurez besoin de comprendre les énoncés suivants :
La formule de De Moivre
Elle énonce que pour tout nombre réel x et tout entier n on a
- (cosx + isinx)n = cos(nx) + isin(nx)
Voir l'article formule d'Euler pour une démonstration.
La formule du binôme de Newton
Elle énonce que pour tout nombre réel x et y et tout entier positif n,
où nous avons les coefficients binomiaux
Elle se démontre par récurrence, voir l'article sur la formule du binôme.
Injectivité de la fonction cotangente carrée
La fonction réelle
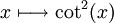
Démonstration : Supposons cot2(x) = cot2(y) pour des certains x et y dans l'intervalle [0,π / 2]. En utilisant la définition de la cotangente pour
![x \in [0,\pi/2]](https://static.techno-science.net/illustration/Definitions/autres/4/421d5aef0497e21c1d81312c40a84c12_87442d6b5ec0026e2488cae63eadf30e.png)
puis l'identité trigonométrique cos2(x) = 1 − sin2(x), nous voyons que sin2(x)(1 − sin2(y)) = sin2(y)(1 − sin2(x)). En soustrayant sin2(x)sin2(y) de chaque côté, nous avons sin2(x) = sin2(y). Comme la fonction sinus est toujours positive sur l'intervalle [0,π / 2], ceci veut dire que sin(x) = sin(y), mais cela est géométriquement évident (en regardant le cercle unité) que la fonction sinus est injective sur l'intervalle [0,π / 2]et donc que x = y.
Nombre de racines d'un polynôme
Si P est un polynôme de degré m, alors P n'a pas plus que m racines distinctes.
Démonstration : ceci est une conséquence de ce que, si r est racine de P, on peut écrire P sous la forme P(X) = (X − r)Q(X) avec Q un polynôme de degré m − 1.
Somme des racines d'un polynôme
Si
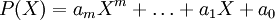
Démonstration : si am = 1, alors P(X) est égal au produit de tous les X − s, où s l'ensemble des racines de P. En développant ce produit, nous voyons que le coefficient de Xm + 1 est l'opposé de la somme de toutes les racines. Si
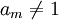
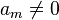
Une identité trigonométrique
L'identité trigonométrique cosec2(x) = 1 + cot2(x)
Démonstration : Ceci découle de l'identité fondamentale cos2(x) + sin2(x) = 1 après avoir été divisé par sin2(x).
Des inégalités
Pour tout nombre réel
![x \in ]0,\pi/2[](https://static.techno-science.net/illustration/Definitions/autres/9/9d95f93176afeddbe3293bb17eaef5e9_beff2f71f6f6e37d033361d72f431bda.png)
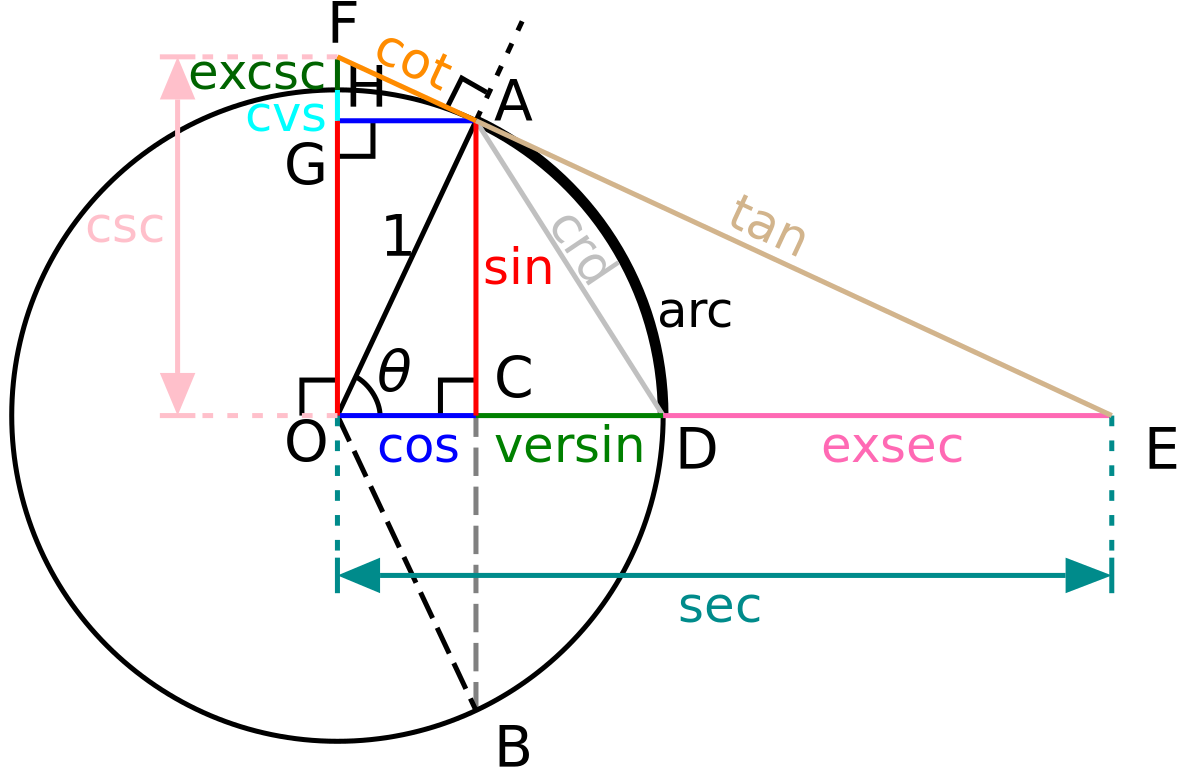
Démonstration : Premièrement, nous avons 0 < sin(x) < x < tan(x). Ceci peut être vu en examinant la figure suivante :
Maintenant, inversons tout cela et élevons au carré. Souvenons-nous que l'inégalité change de sens.
Une limite
Soit a, b, et c des nombres réels, avec a et c tous deux différents de zéro; alors la limite de la fonction (am + b) / (am + c) quand m tend vers l'infini est 1.
Démonstration : Divisons chaque terme par m, nous obtenons
Si nous divisons un nombre fixé par un grand nombre, le quotient tend vers zéro ; ainsi, le numérateur et le dénominateur du dessous tend vers a, et ainsi leur quotient tend vers 1.
Le théorème d'encadrement
Il énonce que si une fonction est « encadrée » entre deux autres fonctions, et que chacune de ces deux fonctions tendent vers une limite commune, alors la fonction « encadrée » tend aussi vers la même limite.
Pour une démonstration, voir Théorème d'encadrement.
La démonstration
L'idée principale derrière la démonstration est de borner les sommes partielles
entre deux expressions, chacune tendra vers π2 / 6 quand m tend vers l'infini. Les deux expressions sont issues des identités impliquant la fonction cotangente et la fonction cosécante. Ces identités découlent à leur tour de la formule de De Moivre, et nous servent à établir ces identités.
Soit
![x\in ]0,\pi/2[](https://static.techno-science.net/illustration/Definitions/autres/9/9d95f93176afeddbe3293bb17eaef5e9_beff2f71f6f6e37d033361d72f431bda.png)
A partir du théorème du binôme, nous avons
En combinant les deux équations et en égalisant les parties imaginaires, nous avons l'identité
Nous prenons cette identité et nous fixons n = 2m + 1, où m est un entier positif, et x = rπ / (2m + 1), où
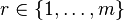
Cette équation est valable pour chacune des valeurs x = rπ / (2m + 1), où
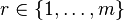
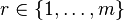
Ce qui veut dire que les nombres cot2(rπ / (2m + 1)), pour
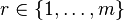
En substituant l'identité cosec2(x) = cot2(x) + 1, nous avons
Maintenant, considérons l'inégalité cot2(x) < 1 / x2 < cosec2(x). Si nous additionnons toutes ces inégalités pour chaque nombre x = rπ / (2m + 1), et si nous utilisons les deux identités ci-dessus, nous obtenons
En les multipliant par [π / (2m + 1)]2, cela devient
Lorsque m tend vers l'infini, la partie gauche et droite tendent chacune vers π2 / 6, donc, par le théorème des gendarmes,
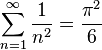
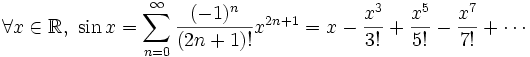
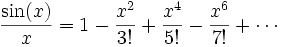
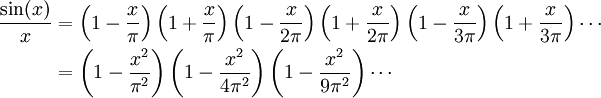
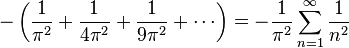
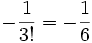
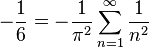
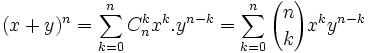
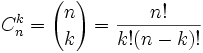
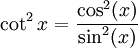
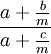
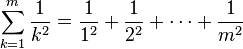
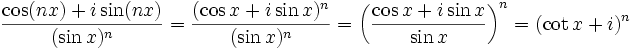
![\begin{align}(\cot x + i)^n &= {n \choose 0} \cot^n x + {n \choose 1} (\cot^{n-1} x)i + \cdots + {n \choose {n-1}} (\cot x)i^{n-1} + {n \choose n} i^n\\&= \left[ {n \choose 0} \cot^n x - {n \choose 2} \cot^{n-2} x \pm \cdots \right] \; + \; i\left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right]\end{align}](https://static.techno-science.net/illustration/Definitions/autres/f/f86dd41a79555544a2dbe796e3fbd95c_4356c0c40f0be090bc131e2372aa99ae.png)
![\frac{\sin (nx)}{(\sin x)^n} = \left[ {n \choose 1} \cot^{n-1} x - {n \choose 3} \cot^{n-3} x \mp \cdots \right]](https://static.techno-science.net/illustration/Definitions/autres/d/db786173c76be69fbf0946a3967e315e_c74ef25c6aa2e6bec63a4a6ac2607bb9.png)