Rémanent de supernova - Définition
La liste des auteurs de cet article est disponible ici.
Désignation des rémanents de supernova
Les rémanents sont aujourd'hui systématiquement catalogués avec le symbole SNR (pour l'anglais SuperNova Remnant), suivi de ses coordonnées galactiques. Divers autres noms sont attribués à certains rémanents, en particulier pour ceux qui ont été détectés avant d'être identifiés comme tels.
Formation et évolution des rémanents
Les rémanents se forment suite à l'explosion d'une étoile en supernova. L'explosion n'est pas forcément sphérique, mais certains rémanents gardent longtemps une forme extrêmement régulière. L'influence d'une source d'énergie interne (un pulsar central) peut affecter significativement la forme et l'évolution du rémanent. Dans l'hypothèse de l'absence d'une source centrale, on distingue essentiellement quatre phases dans la vie d'un rémanent :
- Phase I, expansion libre. La matière éjectée par l'explosion l'est à une vitesse très supérieure à la vitesse de libération de l'astre. Le champ gravitationnel de celui-ci est négligeable, et la matière éjectée n'est pas affectée par celle-ci. Elle se propage ainsi à vitesse constante, emportant sur son passage la matière du milieu interstellaire. Cette phase dure tant que la quantité de matière balayée est petite par rapport à la matière éjectée. Le rayon R du rémanent croît à vitesse constante, sa valeur est proportionnelle au temps :
-
-
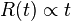
-
- la constance de proportionnalité étant la vitesse de la matière éjectée, qui se compte en milliers de kilomètres par seconde. Le taux d'expansion du rémanent donne l'inverse de son âge. En effet le taux d'expansion,
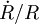
-
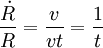
-
- Phase II, expansion adiabatique, dite phase de Sedov-Taylor. La masse de la matière balayée par l'explosion devient significative, voire supérieure à la matière éjectée. Cependant, le transfert de quantité de mouvement entre matière en mouvement et matière interstellaire initialement au repos se fait sans perte d'énergie, d'où le terme d'adiabatique. Le rayon du rémanent croît encore au cours du temps, mais les échanges d'énergie font que cette croissance décélère au cours du temps. Un calcul simple (voir Phase de Sedov-Taylor) donne une dépendance.
-
-
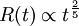
-
- avec une constante de proportionnalité qui ne dépend que de l'énergie dégagée lors de l'explosion et de la densité du milieu interstellaire. Historiquement, cette phase a été étudiée dans le contexte des explosions thermonucléaires atmosphérique. L'inverse du taux d'expansion est cette fois supérieur à l'âge du rémanent, puisque l'on a
-
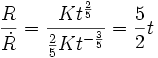
-
- Dans cette phase, l'arrivée du rémanent dans le milieu interstellaire est responsable d'une onde de choc se propageant vers l'extérieur dans le milieu interstellaire, ainsi qu'une onde choc réfléchie se réfléchissant vers le centre. On parle dans ce cas de choc inverse.
- Phase III, pertes radiatives. Cette fois, l'énergie du rémanent est faible, et le choc entre le rémanent proprement dit et le milieu interstellaire provoque des pertes significatives d'énergie. L'expansion du rémanent s'en trouve ralentie, avec une loi de puissance possédant un exposant moindre que le facteur 2/5 de la phase de Sedov-Taylor. Le front avant du rémanent se voit rattrapé par les couches plus internes, moins sujettes aux pertes d'énergie, formant une distribution de matière en coquille.
- Phase IV, disparition. La densité du rémanent devient de l'ordre de celle du milieu interstellaire et l'énergie dégagée par les interactions avec le milieu interstellaire devient faible pour rayonner suffisamment. Le rémanent perd son identité et disparait. Cela se produit quand la vitesse d'expansion du rémanent descend en dessous de quelques kilomètres par seconde.
La transition entre la phase I et la phase II se fait lorsque le volume balayé par le rémanent correspond à une masse de milieu interstellaire de l'ordre de la masse éjectée, soit une masse solaire. Avec une densité typique du milieu interstellaire de l'ordre d'un atome d'hydrogène par centimètre cube, soit une densité de 1,6×10-21 kg/m3, cela se produit quand le rémanent atteint un rayon de l'ordre de 0,7×1017 mètres, soit une petite dizaine d'années-lumière. Avec une vitesse d'expansion alors égale à la vitesse initiale de 10 000 km/s, cela correspond à un âge de quelques milliers d'années.
Le volume balayé par le rémanent supposé sphérique et de rayon R(t)est
-
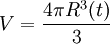
Ce volume correspond à une masse M dans un milieu de densité μ si
-
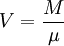
soit quand
-
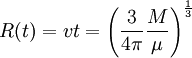
La phase de Sedov Taylor proprement dite dure bien plus longtemps, estimée à quelques centaines de milliers d'années. Cela correspond à un facteur numérique près à la durée d'observabilité d'un rémanent, ceux-ci devenant difficilement observables quand leur énergie devient trop faible. Avec un taux de supernovæ de l'ordre d'une par siècle, l'on s'attend donc à un nombre de rémanents potentiellement observables de l'ordre de quelques milliers. Le nombre de rémanents effectivement identifiés comme tels étant significativement plus faible, pour diverses raisons explicitées ci-dessous.
Le milieu interstellaire étant loin d'être homogène, les rémanents ne sont pas nécessairement de forme sphérique : dès qu'ils entrent dans la phase de Sedov-Taylor, la vitesse d'expansion d'une région du rémanent est reliée à la densité du milieu interstellaire de cet endroit. Les rémanents 3C 58 et la Nébuleuse du Crabe sont des exemples de rémanents non sphériques.
La frontière entre le rémanent et le milieu interstellaire est appelée discontinuité de contact. Cette région est sujette à une instabilité dite « de Rayleigh-Taylor ». Cette instabilité génère de la turbulence à l'interface des deux régions, amplifiant le champ magnétique qui y est présent. Ce champ magnétique provoque en retour une émission radio (par rayonnement synchrotron entre autres). C'est la raison principale pour laquelle les rémanents en coquille présentent un maximum de luminosité à la frontière entre le rémanent et le milieu interstellaire. La situation inverse se produit dans les rémanents pleins, car le gros de l'émission d'énergie ne provient pas de la frontière du rémanent, mais du probable objet central (l'énergie du pulsar du Crabe correspond par exemple à près de 100 000 luminosité solaires).
En l'absence de source d'énergie centrale, l'expansion du rémanent décélère au cours du temps : la vitesse d'expansion reste constante lors de la phase I, puis décroît pendant la phase de Sedov Taylor. Dans ce cas, l'âge du rémanent est toujours inférieur à celui déduit en prenant l'inverse du taux d'expansion. En revanche, en présence d'une source centrale, l'apport d'énergie peut être suffisant pour accélérer l'expansion du rémanent. Dans ce cas, le rémanent peut être plus jeune que ce que son taux d'expansion ne suggère.

















































