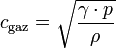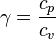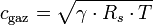Vitesse du son - Définition
La liste des auteurs de cet article est disponible ici.
Vitesse du son dans un corps solide
Dans un solide, la vitesse des ondes mécaniques est dépendante de la masse volumique ρ et des constantes d'élasticité. Dans le cas des ondes de compression se propageant sans engendrer de déformation transverse (cas d'une tige infiniment fine) c'est le module de Young E qui entre en compte, et la vitesse se calcule ainsi :
-
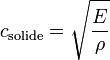
Vitesse du son dans un gaz parfait
La vitesse du son dans un gaz parfait est fonction du coefficient isentropique γ (gamma), de la masse volumique ρ ainsi que de la pression p du gaz, et se calcule ainsi :
avec
cp et cv étant les capacités thermiques massiques isobare et isochore.
La vitesse du son peut être aussi calculée à l'aide de l'équation d'état, du coefficient adiabatique γ (gamma), de la constante spécifique du gaz Rs et de la température T (K en kelvin).
Avec pour l'air :
- γ = 1,4
- Rs = 287 J/kg/K
Le coefficient adiabatique γ dépend peu de la température T, la constante R est une grandeur indépendante de la température.
Cette vitesse est corrélée à la vitesse moyenne <v> des molécules. En effet, l'équation des gaz parfaits relie p à la température T et au volume V, et l'on a
- pV γ = constante
Ce qui permet d'exprimer c en fonction de T seul, et donc de <v> Dans le cas d'un gaz parfait monoatomique (γ = 5/3), on a :
-
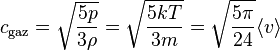
- cgaz ≈ 0,81·<v'>
m étant la masse d'une molécule.
Cette relation indique que dans le domaine des gaz parfaits (c'est-à-dire des pressions modérées), la vitesse du son est proportionnelle à la vitesse des molécules, c'est-à-dire à la racine carrée de la température absolue.
Dans le cas de l'air (composé en majorité de gaz parfaits diatomiques), la célérité du son peut être approchée par la linéarisation suivante :
- cair = (331,5 + 0,607·θ) m/s
où θ (thêta) est la température en degrés Celsius :
- θ = T-273,15
T étant en K.
Cette formule approchée permet d'obtenir la célérité du son de -20 °C à +40 °C avec une erreur inférieure à 0,2 %.
Influence des autres facteurs
L'humidité de l'air influe peu.
Vitesse du son dans un liquide
La célérité du son dans un liquide est une fonction de la masse volumique ρ et du coefficient de compressibilité adiabatique χ et se calcule ainsi:
-
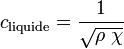
Fluides diphasique
Dans le cas d'un fluide diphasique (bulle d'air dans l'eau par exemple), la vitesse du son se trouve fortement modifiée. Le calcul de la vitesse du son est alors assez complexe et dépend notamment des relations qui unissent les deux fluides (par exemple, dans le cas d'un liquide avec des bulles de vapeur, il faudra prendre en compte les changements de phase).
Néanmoins, un résultat général peut être tiré. La vitesse du son de ce mélange est bien inférieure à la plus petite des deux. Par exemple, pour un mélange eau/vapeur, la vitesse du son est autour de 30 m/s pour un taux de présence de 0,5.
Table des propriétés de l'air en fonction de la température
La table suivante présente l'évolution de quelques propriétés de l'air sous une pression d'une atmosphère en fonction de la température.
| θ en °C | c en m/s | ρ en kg/m³ | Z en N·s/m³ |
|---|---|---|---|
| - 10 | 325,4 | 1,341 | 436,5 |
| - 5 | 328,5 | 1,316 | 432,4 |
| 0 | 331,5 | 1,293 | 428,3 |
| + 5 | 334,5 | 1,269 | 424,5 |
| + 10 | 337,5 | 1,247 | 420,7 |
| + 15 | 340,5 | 1,225 | 417,0 |
| + 20 | 343,4 | 1,204 | 413,5 |
| + 25 | 346,3 | 1,184 | 410,0 |
| + 30 | 349,2 | 1,164 | 406,6 |