Constante cosmologique - Définition
La constante cosmologique est un paramètre rajouté par Einstein en février 1917 à ses équations de la relativité générale (1915), dans le but de rendre sa théorie compatible avec l'idée qu'il avait alors d'un Univers statique. Après la découverte en 1929 du décalage vers le rouge par Edwin Hubble impliquant un Univers en expansion, Albert Einstein revient sur l'introduction de la constante cosmologique, la qualifiant de " plus grande bêtise de sa vie. " Néanmoins des découvertes récentes durant les années 1990, traitant des problèmes tels que l'énergie du vide, la théorie quantique des champs ou l'accélération de l'expansion de l'Univers ont provoqué un regain d'intérêt pour ce paramètre, qui est par ailleurs compatible avec l'ensemble de la théorie de la relativité générale.
Description mathématique
NB Cet article suit les conventions de signe classiques de MTW [1]
Cet article adopte également la convention de sommation d'Einstein.
On considère un espace-temps caractérisé par le tenseur métrique gμν de signature (-, +, +, +). On note Rμν le tenseur de Ricci associé, et
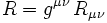
Introduction
La constante cosmologique est le terme mathématique noté Λ qui apparaît dans l'équation d'Einstein, à partir de laquelle tous les modèles cosmologiques sont dérivés :
|
|
G la constante gravitationnelle (environ 6,6742 × 10-11 m3 kg-1 s-2), c la vitesse de la lumière (exactement 299 792 458 m s-1) par définition, et Tμν le tenseur énergie-impulsion.
Mathématiquement, le membre de gauche de cette équation, qui représente la géométrie de l'espace-temps, est la forme la plus générale d'un tenseur covariant dont la dérivée covariante soit identiquement nulle. En effet, lorsque la connexion est associée à la métrique, on a :
|
|
et les identités de Bianchi s'écrivent :
|
|
On en déduit que le tenseur énergie-impulsion, qui décrit la distribution de matière et énergie dans l'espace-temps, est conservé (de façon covariante) :
|
|
Interprétation physique
Le terme contenant la constante cosmologique peut se placer à droite de l'équation en changeant son signe, et l'égalité reste bien évidemment vérifiée :
|
|
Cependant, de ce côté droit, le terme prend une signification différente, puisqu'il est du " côté de l'énergie-impulsion ". On cherche alors une forme d'énergie que le tenseur d'énergie-impulsion décrivant la matière et/ou le rayonnement ordinaires ne contiendrait pas, mais qui serait décrit par le terme de constante cosmologique :
|
|
Cette expression est celle d'un fluide parfait [ST02] dont la densité d'énergie volumique serait :
|
|
c'est-à-dire que sa masse volumique ρΛ vaudrait :
|
|
et dont la pression serait négative :
|
|
La constante cosmologique contribue ainsi à ce que l'on appelle l'énergie du vide.
Limite newtonienne
Equations d'Einstein en champ faible
On se place à la limite des champs faibles :
|
|
où ημν est la métrique plate de Minkowski. Dans cette limite, le tenseur de Ricci s'écrit au premier ordre :
|
|
Considérons alors un espace-temps statique, dont la métrique se met sous la forme :
|
|
Dans ce système de coordonnées, seule la composante temporelle-temporelle du tenseur de Ricci est non-négligeable à la limite des champs faibles. Elle s'écrit simplement :
|
|
où Δ est l'opérateur de Laplace-Beltrami à trois dimensions, calculé avec la partie spatiale gij(xk) de la métrique.
Application au fluide parfait
Si l'on remplit l'univers statique précédent d'un fluide parfait au repos dont la masse volumique est ρ (c'est-à-dire que sa densité volumique d'énergie vaut
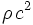
|
|
On a vu plus haut que :
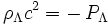
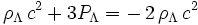
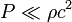
|
|
où V est le potentiel Newtonien de gravitation (
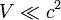
|
|
Pour un fluide réel, la masse volumique est toujours positive et l'effet gravitationnel est toujours attractif. En revanche, avec une constante cosmologique positive, la masse volumique associée est aussi positive, et la présence du signe " moins " entraîne un effet gravitationnel répulsif.
Le retour de la constante cosmologique
Un temps abandonnée, la constante cosmologique a été récemment remise au goût du jour après la découverte de l'accélération de l'expansion de l'univers. Elle décrirait une force, encore hypothétique, qui accélererait l'expansion de l'univers, appelée énergie sombre (à ne pas confondre avec la matière noire).
En novembre 2005, le USPTO a accordé un brevet ayant pour objet un vaisseau spatial dont la propulsion repose sur la modification locale de la constante cosmologique par la mise œuvre de matériaux supraconducteurs. Le but est de créer localement des conditions d'anti-gravité. Notons cependant que la communauté scientifique semble sceptique quant au réalisme d'un tel dispositif en raison de la quantité d'énergie colossale qui serait nécessaire.[réf. nécessaire]
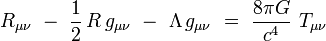
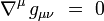
![\nabla^{\mu} \, \left[ \, R_{\mu\nu} \ - \ \frac{1}{2} \, R \, g_{\mu\nu} \, \right ] \ = \ 0](https://static.techno-science.net/illustration/Definitions/autres/e/e38f040039e26eb1cdef57031af4d132_b486679ce2cdec0e0dbc72b76b8d38c5.png)
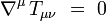
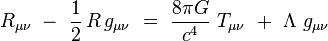
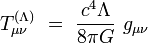
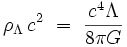
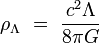
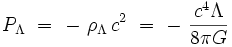
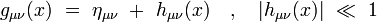
![R_{\mu \nu}(x) \ = \ [ \dots ]](https://static.techno-science.net/illustration/Definitions/autres/d/d6d69ac32654910a86ac9d50efb8a902_bcb5bcfa3477e3e66fb895c33ac260d4.png)
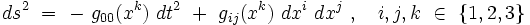
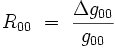
![\frac{\Delta g_{00}}{g_{00}} \ = \ \frac{8\pi G}{c^4} \ \left[ \ ( \rho \, c^2 + 3 P ) \ + \ ( \rho_{\Lambda} \, c^2 + 3 P_{\Lambda} ) \ \right]](https://static.techno-science.net/illustration/Definitions/autres/3/35324b2ddca969554b27d767144ed4fb_2046645de42691a6c67f37271c10af34.png)
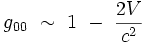
![\Delta \, V \ = \ 4 \pi G \ \left[ \ \rho \ - \ 2 \, \rho_{\Lambda} \ \right]](https://static.techno-science.net/illustration/Definitions/autres/5/5b888d099ed0750e58104f563df8ecf9_5193ae53f06d29cf66b0bc2c5a073aef.png)

















































