Référentiel galiléen - Définition

En physique, un référentiel galiléen est un référentiel dans lequel un objet isolé (sur lequel ne s'exerce aucune force ou sur lequel la résultante des forces est nulle) est soit immobile, soit en mouvement de translation rectiligne uniforme par rapport à ce référentiel. Cela signifie que le principe d'inertie, qui est énoncé dans la première loi de Newton s'applique.

Si un référentiel est animé d'un mouvement accéléré par rapport à un référentiel galiléen, il faut alors faire intervenir les forces d'inertie.

Les référentiels galiléens, aussi parfois appelés référentiels inertiels, sont nommés ainsi en hommage à Galilée et plus particulièrement à la relativité galiléenne.

Application des référentiels galiléens

Les référentiels galiléens sont employés en mécanique newtonienne et en relativité restreinte.

• En mécanique newtonienne, tous les repères galiléens sont supposés équivalents : si deux observateurs O et O’ sont animés d'un mouvement de translation uniforme l'un par rapport à l'autre, alors les mêmes lois du mouvement doivent s'appliquer à chacun d'eux, que O soit supposé être la référence "immobile" (auquel cas O’ est en mouvement) ou que l'on suppose O’ immobile et O en mouvement. Dans le cadre de la mécanique newtonienne, le temps s'écoule, par hypothèse, au même rythme pour tous les observateurs signifiant qu'une horloge calibrée dans un référentiel continuera à mesurer des durées exactes dans tout autre référentiel, que celui-ci soit galiléen ou non.

• Dans la relativité restreinte, l'équivalence des référentiels galiléens est aussi supposée valide. Toutefois, l'hypothèse de temps absolu valable dans tous les référentiels est remplacée par l'hypothèse d'invariance de la vitesse de la lumière, laquelle est la même dans tout référentiel galiléen. Cela a nécessité la mise en place d'un édifice théorique, initié par Henri Poincaré (1900) en relation avec la notion de temps local élaborée par Hendrik Lorentz et conçu, apparemment indépendamment, par Albert Einstein. Cette théorie permet à des observateurs de définir des temps et des distances apparents sur la base de l'hypothèse d'invariance de la vitesse de la lumière dans chacun de leur référentiel et de construire un système de coordonnées étendu (l'espace-temps) pour mesurer le temps et la distance qui séparent deux évènements. Ainsi des observateurs situés dans des référentiels différents vont obtenir une séparation en temps et en espace différente entre deux mêmes évènements. Les formules pour convertir ou " transformer " les valeurs entre différents référentiels galiléens permettent à chaque observateur de calculer comment les lois de la physique se modifient quand elles sont observées dans un autre référentiel. Ainsi, selon le point de vue choisi, le temps et la distance qui séparent deux évènements peuvent changer, mais l'intervalle d'espace-temps lui est inchangé : il est indépendant du référentiel galiléen choisi, c'est un invariant.

Changement de référentiel

Un changement de référentiel est l'ensemble des lois à appliquer pour convertir les grandeurs physiques d'un référentiel à un autre. Dans le cas où la conversion porte sur les distances et les durées, on parle de transformation.

Mécanique newtonienne

Dans le cadre de la mécanique newtonienne, on montre que deux référentiels galiléens sont nécessairement animés d'un mouvement relatif de translation rectiligne uniforme. Leur vitesse relative est donc constante en norme, en sens et en direction. Considérons pour cela deux référentiels galiléens : l'un lié à un observateur O, l'autre lié à un observateur O’. Considérons de plus un corps C qui n'est soumis à aucune force alors, en vertu de la première loi de Newton, le corps C a un mouvement rectiligne uniforme dans chacun des deux repères galiléens O et O’, ce que l'on peut écrire sous forme vectorielle :

et où et sont des constantes.

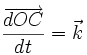
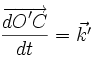
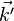
La distance de l'observateur O à l'observateur O' peut être exprimée aussi bien dans un référentiel que dans l'autre. La mécanique classique pose comme hypothèse que ne dépend pas du référentiel dans lequel on le mesure^[1]. Cela est aussi vrai pour et et de ce fait, la relation vectorielle suivante est vraie dans tout référentiel (qu'il soit galiléen ou non) :

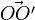
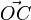
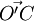
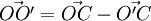
D'autre part, en mécanique classique, le temps est absolu, lui aussi indépendant du référentiel choisi. Par conséquent les dérivées des vecteurs OC et O’C sont calculées par rapport à la même variable temporelle t et l'on peut donc déduire le mouvement relatif de O par rapport à O’ :

Qui signifie, par définition, que les référentiels galiléens O et O’ sont animés d'un mouvement rectiligne uniforme l'un par rapport à l'autre CQFD.

De cette relation on déduit la transformation de Galilée, laquelle permet de définir une relation d'équivalence entre les référentiels.

Relativité restreinte

Einstein a affirmé que si la lumière se propage à la vitesse c dans un unique référentiel absolu (comme cela fut postulé en physique pré-relativiste où l'on supposait l'existence d'un éther), alors les transformations d'espace et de temps se font à l'aide de la transformation de Galilée. En revanche, dans le cas de la relativité restreinte, c'est la transformation de Lorentz qui s'applique, laquelle coïncide avec la transformation de Galilée pour des vitesses relativement faibles par rapport à la vitesse de la lumière.

Cas de la théorie de la relativité générale

La théorie de la relativité générale d'Einstein traite des référentiels accélérés en remplaçant l'espace euclidien " plat " de la relativité restreinte par une géométrie non-euclidienne " courbée ". En relativité générale, le principe d'inertie est remplacé par le principe d'équivalence qui postule que la masse inertielle et la masse pesante sont identiques. Une conséquence de ce principe est que les objets se déplacent selon des géodésiques et qu'il n'est plus acquis que des objets isolés conserveront indéfiniment un mouvement relatif rectiligne uniforme. Ce phénomène de déviation signifie que les référentiels galiléens sont locaux et non plus globaux comme c'est le cas en mécanique newtonienne ou en relativité restreinte.

Toutefois, la relativité générale peut coïncider avec la relativité restreinte sur des petites régions de l'espace-temps où les effets de courbure sont moins importants, auquel cas les raisonnements liés aux référentiels galiléens peuvent de nouveau être appliqués. À la suite de quoi, la relativité restreinte est parfois décrite comme une " théorie locale " de la relativité générale (cela ne concerne toutefois que l'application de la théorie et non pas une relation établie).

Analyse critique de la notion de référentiel galiléen

La référence aux lois du mouvement de Newton n'établit pas à elle seule la cohérence. On commence par choisir un système isolé : la résultante des forces qui lui sont appliquées est nulle. On définit ensuite un référentiel galiléen : la vitesse du système isolé par rapport à un tel référentiel est constante. Tout cela fonctionne fort bien, mais comment définit-on une force? Comment peut-on décider si un système est soumis à un ensemble de forces dont la résultante est nulle ? La seule réponse possible consiste à vérifier que son mouvement est rectiligne et uniforme par rapport à un référentiel galiléen (!) Il faut donc se donner au départ un référentiel galiléen choisi arbitrairement.

Newton s'en sort assez bien en apparence en affirmant l'existence d'un espace absolu (et donc implicitement galiléen). Tous les référentiels dits "galiléens" sont donc en mouvement rectiligne et uniforme par rapport à un référentiel lié à l'espace absolu, et donc les lois de Newton peuvent s'exprimer dans un cadre formel absolu. Elles ne servent plus à qualifier un référentiel comme "galiléen", mais servent au contraire à décider si un système est isolé ou non. On peut alors tolérer l'expression "référentiel galiléen" bien que celle-ci relève d'un abus de langage. La conséquence immédiate de cet abus est cependant assez sournoise car elle autorise l'assignation d'un "état de mouvement" comme propriété intrinsèque d'un système : par exemple on affirmera qu'un système est "en mouvement accéléré", ce qui relève d'une erreur catégorielle.

Tout l'édifice s'écroule dès que l'on s'abstient de postuler l'existence d'un espace et d'un temps absolus. La théorie de la relativité restreinte n'échappe pas à une double circularité de son postulat fondateur. D'une part le triplet de propriétés associées à un système "qui n'est soumis à aucune force", "isolé", "en mouvement galiléen" est défini circulairement comme exposé ci-dessus, et d'autre part, on doit faire référence à des notions physiques telles que la "force" pour poser le cadre spatio-temporel formel sur la base duquel on entend ériger une théorie physique, et en particulier la notion de "force". Il est alors parfaitement clair que l'expression "état de mouvement" ne peut plus désigner une propriété intrinsèque d'un système, mais seulement une relation entre le système et un certain référentiel. L'abus de langage "référentiel galiléen" relève ici encore d'une erreur catégorielle.

La solution de cet imbroglio est esquissée plus haut: "il faut se donner au départ un référentiel galiléen arbitrairement choisi". Faire "comme si" il s'agissait de l'espace absolu de Newton. Mais au lieu de se satisfaire de ce point de vue situé, il faut construire "le point de vue de nulle part", c'est-à-dire extraire l'invariant de tous les points de vue situés, dont chacun reflète un choix particulier du référentiel "pseudo-absolu" de départ. On peut alors créer la notion de "classe d'équivalence galiléenne" stipulant que deux référentiels sont équivalents au sens "galiléen" du terme si et seulement si leur mouvement relatif est rectiligne et uniforme. L'accélération devient alors une notion relative permettant de différencier ou de comparer les classes d'équivalence. Une théorie "relativiste" exigerait alors que les "lois de la physique" exprimées dans divers référentiels appartenant à une même classe puissent seulement différer par la valeur de la vitesse relative de ces référentiels. Et si elles étaient exprimées dans des référentiels appartenant à des classes différentes, elles ne pourraient différer que par la valeur de l'accélération relative entre les classes et les vitesses relatives entre les référentiels.

Notes