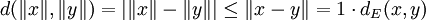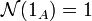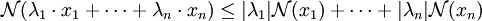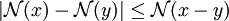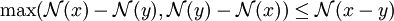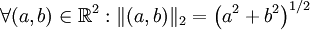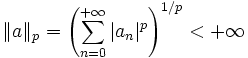Norme (mathématiques) - Définition
En mathématiques, une norme est une fonction qui donne un sens à l'idée usuelle de longueur d'un vecteur, a priori sans recourir à un produit scalaire. L'intérêt de cette notion est d'être valable aussi bien pour les espaces de dimensions finie que pour les espaces de fonctions. Il y a plusieurs façons de définir de telles normes sur un espace vectoriel, et le choix d'une norme adaptée à un problème d'analyse est une étape importante dans sa résolution.
Définitions
Norme sur un espace vectoriel
Soit


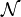
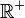
- Séparation :
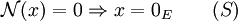
- Homogénéité :
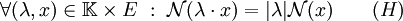
- Inégalité triangulaire :
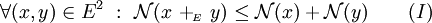
Habituellement, l'image d'un vecteur x par une norme se note
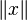
-
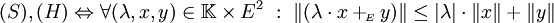
- (H) permet la réciproque de (S).
- (H) rend la norme symétrique:
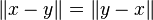
E est alors appelé espace vectoriel normé (parfois abrégé EVN).
Remarque : cette définition s'étend mot pour mot aux espaces vectoriels sur un corps valué complet. Dans ce cas, certaines normes appelées ultramétriques vérifient une condition plus forte que l'inégalité triangulaire.
Norme d'algèbre
Supposons
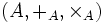

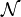
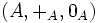
-
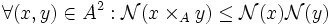
alors
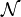
Exemple : sur l'algèbre
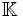
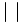
Relations fondamentales
L'inégalité triangulaire entraîne (par récurrence immédiate)
et se " renverse " sous la forme
En effet:
-
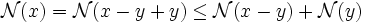
-
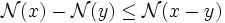
De même:
-
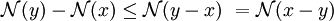
enfin:
Norme euclidienne et produit scalaire
Tout produit scalaire sur

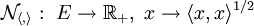
Cette norme est appelée la norme euclidienne associée au produit scalaire.
Exemples
Espaces normés de dimension finie
Normes canoniques sur Kn
L'espace
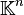
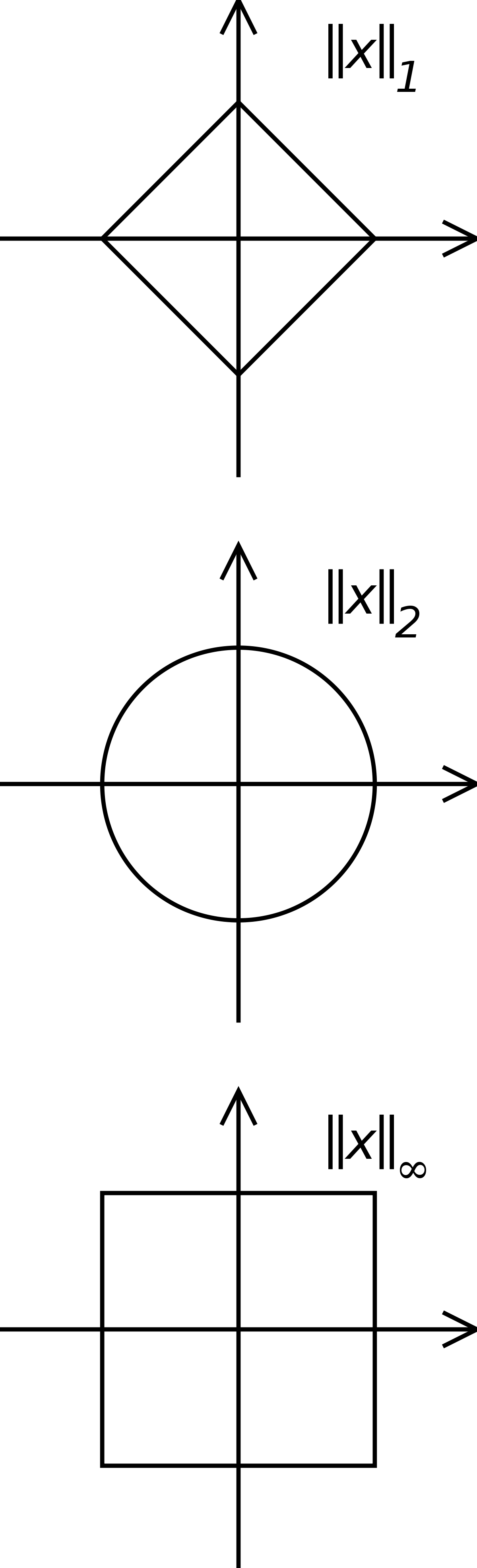
- Norme-infini
- Soit
![\ x=(x_1,\dots,x_n)\in\mathbb K^n: \|x\|_\infty = \max_{i\in[1,\dots,n]}|x_i|](https://static.techno-science.net/illustration/Definitions/autres/f/fdadfc573c6f1e8e4390822507396415_aa4722c452ac5fcfdabd4428c712f352.png)
- Norme-1
- Soit
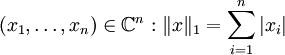
-
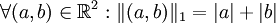
-
- Norme-2
- Soit
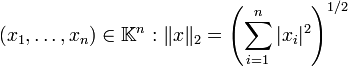

-
- Norme-p
- Soit
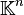
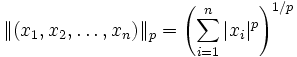
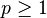
- C'est un espace vectoriel normé.
La notation
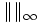
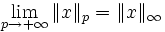
Ceci correspond à la norme habituellement utilisée pour la distance entre deux points dans le plan ou l'espace géométrique.
Autres espaces de dimension finie
Tout

En effet, E est isomorphe à
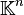
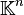
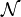
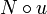
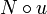
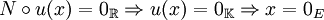
Cercles carrés
Bertrand Russell aimait à donner comme exemple d'oxymore l'expression " cercle carré ". S'il s'agit bien d'un oxymore en géométrie euclidienne, les cercles carrés existent bel et bien lorsqu'on adopte par exemple la norme infinie. L'ensemble des points de norme 1 est un carré incliné à 45° et est un cercle dans la mesure où tous leurs points sont à égale distance de l'origine.
Espaces normés de dimension infinie
- L'ensemble
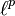
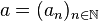
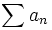
-
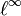
-
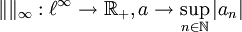
- Le

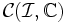
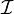


-
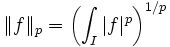
- et de la norme-infini :
-
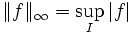
- que l'on retrouve avec:
-
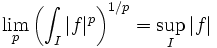
- On l'appelle également norme de la convergence uniforme.
- L'algèbre
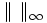
- L'algèbre
![\mathbb K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/11cf18672fa8c102e5d2ec8bdfe203c8_bd379140d6a603f16bfb95868779a783.png)

- Soit
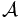

-
![\forall P \in\mathbb K[X]:\ \sup|P(\mathcal A)|=\| P \|_\infty^{\mathcal A}](https://static.techno-science.net/illustration/Definitions/autres/b/bae5b6a894e3e2395dd8031c07af4b2c_07748b64793f6e22727a79b7fa9fc479.png)
- construit alors
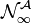
![\mathbb K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/11cf18672fa8c102e5d2ec8bdfe203c8_bd379140d6a603f16bfb95868779a783.png)
Topologie induite
Un espace vectoriel normé
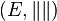
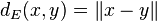
On appelle espace de Banach un espace vectoriel normé complet. Une algèbre normée complète est dite algèbre de Banach.
Continuité de la norme
En notant d la distance canonique de


-