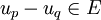Suite de Cauchy - Définition
En analyse mathématique, une suite de Cauchy est une suite de réels, de complexes, de points d'un espace métrique, ou d'un espace topologique uniforme dont les termes se rapprochent à partir d'un certain rang. Ces suites sont celles susceptibles de converger. Elles sont au centre de la définition de complétude. Les suites de Cauchy portent le nom du mathématicien français Augustin Louis Cauchy.
Il existe une notion équivalente pour les filtres : les filtres de Cauchy.
Suite réelle ou complexe de Cauchy
La différence des termes consécutifs de la suite (ln(n)) tend vers 0. On peut préciser la vitesse de convergence :
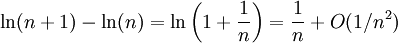
Cependant, ln(2n) − ln(n) = ln(2) ne converge pas vers 0 lorsque n tend vers l'infini. Cette constatation mesure un défaut de non convergence de la suite ln(n) et conduit à énoncer un critère de convergence, le critère de Cauchy.
Une suite de réels ou de complexes est dite de Cauchy lorsque les termes de la suite se rapprochent uniformément les uns des autres en l'infini au sens où :
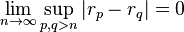
Cette dernière condition se réécrit classiquement à l'aide de quantificateurs universels et existentiels :
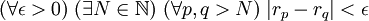
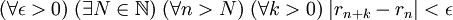
Critère de Cauchy : Une suite {rn} de nombre réels ou complexes converge si et seulement si c'est une suite de Cauchy.
Suite de Cauchy dans un espace métrique
Définition
Une suite
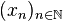
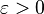
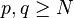

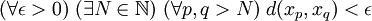
Les inégalités peuvent être prises indifférement larges ou stricites. Lorsque certains ouvrages introduisent la notion de suite de Cauchy uniquement pour les suites de réels, c'est exactement la même définition. La distance d est simplement à remplacer par la valeur absolue de la différence.
Intuitivement, les termes de la suite deviennent de plus en plus proches les uns des autres d'une certaine façon qui suggère que la suite doit avoir une limite dans l'espace. Les suites convergentes sont effectivement de Cauchy, mais néanmoins la réciproque n'est pas vraie en toute généralité. Par exemple, il existe des suites de rationnels qui sont de Cauchy dans
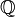
Exemple : l'ensemble A des nombres rationnels r tels que
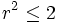
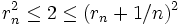
C'est la raison pour laquelle un espace métrique dans lequel toute suite de Cauchy converge est dit complet. L'ensemble des nombres réels est complet, et la construction standard de l'ensemble des nombres réels utilise les suites de Cauchy de nombres rationnels (voir la construction des nombres réels à ce sujet).
Propriétés
- Dans un espace métrique, toute suite convergente est de Cauchy.
Supposons qu'une suite x = (xn) d'un espace métrique (X,d) converge vers une limite l. Alors, pour tout ε > 0, il existe un entier N suffisamment grand tel que pour tout n>N on a : d(xn,l) < ε. L'inégalité triangulaire implique que pour p,q>N, on a :
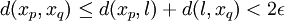
La suite x est donc bien de Cauchy.
- Toute suite de Cauchy est bornée.
Soit (xn) une suite de Cauchy. Appliquons la définition pour ε = 1. Il existe un entier naturel N vérifiant d(xp,xq) < 1 pour
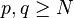
- Une suite de Cauchy a au plus une valeur d'adhérence. Si elle possède une valeur d'adhérence, alors elle converge.
Une suite convergente dans un espace métrique possède une unique valeur d'adhérence, à savoir sa limite. La première affirmation découle de fait de la seconde. Soit x une suite de Cauchy de (X,d) admettant une valeur d'ahérence l. Démontrons que x converge vers l. Choississons un réel arbitraire ε > 0. Comme x est une suite de Cauchy, il existe un entier naturel N tel que pour tous p, et q>N, on a : d(xp,xq) < ε. Mais l est la limite d'une certaine suite extraite de (xn), qu'on note
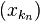
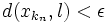
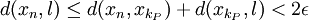
Un tel entier N pouvait être défini pour tout réel ε > 0, la suite x converge vers l.
- L'image d'une suite de Cauchy par une application uniformément continue est de Cauchy.
Soit f une application uniformément continue d'un expace métrique (X,dX) vers (Y,dY), et soit x une suite de Cauchy de (X,dX). Fixons ε > 0. Comme f est uniformément continue, il existe η > 0 tel que, pour tous x et x' de X, on a :
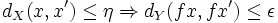
Comme x est de Cauchy, il existe un entier naturel N tel que pour tous p, q>N, on a : dX(xp,xq) < η. A fortiori, pour p, q>N, on a par l'implication ci-dessus : dY(fxp,fxq) < ε. La suite (f(xn)) est donc elle-même de Cauchy.
- Dans les espaces vectoriels normés, les suites de Cauchy forment un sous-espace de l'espace des suites.
Une homothétie d'un espace vectoriel normé est une application lipschitzienne, donc uniformément continue. L'image d'une suite de Cauchy par une application uniformément continue étant de Cauchy, si x est une suite de Cauchy d'un espace vectoriel normé E et r est un réel, alors r.x est une suite de Cauchy. De même, la somme de deux suites de Cauchy de E est une suite de Cauchy de E : la somme vectorielle définit une application uniformément continue
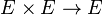
- Dans une algèbre normée, un produit de suites de Cauchy est de Cauchy.
Considérons deux suites de Cauchy x et y dans une algèbre normée
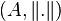
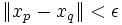
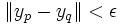
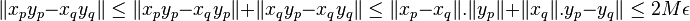
La seconde inégalité provient de la sous-multiplicativité de la norme. La suite xy est donc de Cauchy.
- Dans un espace ultramétrique (X,d), une suite (xn) est de Cauchy ssi
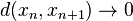
Seul le sens réciproque n'est pas toujours vérifié et utilise l'inégalité ultramétrique. Supposons donc
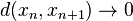
![d(x_n,x_{n+k+1})\leq \max\left[d(x_n,x_{n+1}),d(x_{n+1},x_{n+1+k})\right]\leq \epsilon](https://static.techno-science.net/illustration/Definitions/autres/9/9a100726fd172d8de92527d4c9855c31_fc456e9b831d98884623794d8d16dfcc.png)
La seconde inégalité provient de l'application de l'hypothèse de récurrence.
Approche non standard
En analyse non standard, pour un espace métrique standard (X,d), il existe une définition équivalente mais pratique de la notion de suite de Cauchy.
- Dans un espace métrique standard (X,d), une suite standard x est de Cauchy est de Cauchy ssi pour tous entiers naturels non standards n et p, le réel d(xp,xq) est infiniment petite :
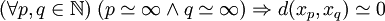
En effet, si x est une suite de Cauchy, alors pour tout réel ε > 0, il existe un entier N(ε) tel que pour tous p, q>N, on a : d(xp,xq) < ε. Si ε est un réel standard, le principe de transfert permet d'imposer à N(ε) d'être un entier standard car la suite x est standard. Or tout entier naturel non standard est strictement plus grand que tout entier naturel standard. Donc, si p et q sont des entiers non standards, ils sont plus grands que tous les N(ε). De suite, d(xp,xq) est strictement inférieurs à tous les réels standards strictement positifs ; c'est donc un infiniment petit.
Réciproquement, supposons que pour tous entiers non standards p et q, le réel d(xp,xq) est un infiniment petit. Fixons dans un premier temps N un entier non standard. Tout entier plus grand que N est aussi non standard. Soit ε > 0 un réel standard. Alors pour p et q>N, on a : d(xp,xq) < ε. De fait, l'assertion suivante :
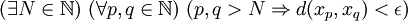
est vérifiée pour tout réel standard strictement positif ε. Par principe de transfert, elle est vérifiée pour tout ε > 0, ce qui signifie exactement que x est de Cauchy.
Suite de Cauchy dans un espace uniforme
Définitions
Dans un espace uniforme, une suite (xn) est dite de Cauchy lorsque pour tout écart continu d sur X, il existe un entier naturel N tel que pour tout p,q > N, on a : d(xp,xq) < 1.
Une famille (xα) dans un espace uniforme X est une famille de Cauchy si pour tout voisinage V il existe un nombre α0 tel que pour tous α, β > α0, le couple (xα, xβ) soit dans V2.
Dans des exemples pratiques :
- Dans un groupe topologique G, une suite (gn) est dite de Cauchy lorsque, pour tout voisinage V de l'élément neutre, il existe N tel que pour tous p,q > N on a :
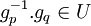
- Dans un espace vectoriel topologique localement convexe E, une suite de vecteurs (un) est dite de Cauchy lorsque pour tout voisinage convexe V de 0, il existe un entier naturel N tel que pour tous p, q>N on a :