Programme de Hamilton - Définition
Le programme de Hamilton est une idée de " plan d'attaque ", due à Richard Hamilton, de certains problèmes en topologie des variétés, notamment la célèbre conjecture de Poincaré.
Nous allons essayer de décrire ici, sans rentrer dans les détails, les raisons d'être de ce programme.
Idée naïve
Dans son article fondateur de 1982, Three-manifolds with positive Ricci curvature, Richard Hamilton introduit le flot de Ricci. Celui-ci est une équation aux dérivées partielles portant sur le tenseur métrique d'une variété riemannienne : On part d'une métrique g0, que l'on fait évoluer par :
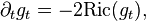
où Ric est la courbure de Ricci de la métrique.
Il est facile de vérifier que les variétés à courbure constante, c'est-à-dire celles munies d'une métrique d'Einstein, sont des solitons ou des points fixes généralisés du flot : le flot de Ricci n'agit sur eux que par une dilatation.
On peut alors penser (et les premiers résultats d'Hamilton sur les variétés de dimension 3, ainsi que sur les courbes et surfaces confirment cette impression) que, de même que l'équation de la chaleur a tendance à homogénéiser une distribution de température, le flot de Ricci va " tendre " à homogénéiser la courbure de la variété.
Pour attaquer certains problèmes de topologie, Hamilton pense donc à prendre une variété, la munir d'une métrique riemannienne, laisser agir le flot et espérer récupérer une variété munie d'une métrique à courbure constante. Par exemple, si on part d'une variété simplement connexe, et qu'on récupère ainsi une variété simplement connexe de courbure constante strictement positive, on saura que la variété n'est autre que la sphère.
Nuançons ce propos : même dans la version la plus naïve de son programme, Richard Hamilton n'a jamais pensé obtenir aussi facilement des résultats de topologie. On peut fort bien imaginer que le flot s'arrête en un temps fini, parce que la courbure de la variété explose, soit globalement, soit localement. L'idée serait alors de comprendre et de classer de telles " singularités ", et de réussir, à l'aide de découpages, à obtenir plusieurs variétés sur lesquelles on pourrait relancer le flot. L'espoir est qu'in fine, on arrive, après un nombre fini de découpages, à des morceaux à courbure constante. On obtiendrait ainsi, " à la limite ", si tout se passe bien, des morceaux de variétés dont on pourrait connaître certaines propriétés topologiques. Notre variété de départ serait donc obtenue en " recollant " ces morceaux sympathiques, ce qui ouvre une voie d'accès aux célèbres conjectures de topologie, comme la conjecture de Thurston.
Existence en temps petit
Comme toute ÉDP, l'équation du flot de Ricci ne vérifie pas a priori de principes d'existence et d'unicité qui soit comparable au théorème de Cauchy-Lipschitz pour les ÉDO. Le premier travail d'Hamilton a été de prouver que ce flot existe en temps petit.
Osons une comparaison : on sait que pour l'équation de la chaleur, il existe une unique solution en tous temps, et qu'elle est infiniment dérivable. Or, par certains côtés (la parabolicité), le flot de Ricci ressemble à l'équation de la chaleur. Les équations paraboliques possèdent une théorie générale développée, qui assure l'existence en temps petit de solutions. Cependant, l'équation du flot de Ricci n'est pas à proprement parler parabolique : elle n'est que faiblement parabolique : l'existence et l'unicité en temps petit ne sont donc pas garanties par un résultat général.
Un des premiers résultats de Hamilton, et de loin le plus fondamental dans l'étude du flot est donc de prouver ce résultat : il y parvint dans l'article déjà cité, en utilisant l'artillerie du théorème d'inversion de Nash-Moser. Cependant, de Turck parvint au même résultat dans son article Deforming metrics in the direction of their Ricci tensors de 1983, paru dans le Journal of Differential Geometry, en se ramenant astucieusement à la théorie générale des équations strictement paraboliques.
Principes du maximum
Un des outils analytiques principaux de l'étude du flot de Ricci est l'ensemble des principes du maximum. Ceux-ci permettent de contrôler certaines quantités géométriques (principalement mais pas uniquement les courbures) en fonction de leurs valeurs au départ du flot. Plus utilement qu'une longue glose, nous allons énoncer le plus simple d'entre eux : le principe du maximum scalaire.
Soit (M,g) une variété riemannienne et (gt)t une famille de métriques solutions du flot de Ricci sur l'intervalle [0,t0] et
![u : M \times [0,t_0] \to \mathbb R](https://static.techno-science.net/illustration/Definitions/autres/2/20797c4c1c795c7e4d45ab3e47d7ddf8_d21523fa28aabacaf5af35fb2487a704.png)
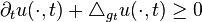
![t \in [0,t_0]](https://static.techno-science.net/illustration/Definitions/autres/f/f00df28eda61f6a374a9d0c19999a3be_0a560e2bcd147d8a61af4753d6dd845e.png)
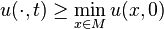
Il existe des versions plus compliquées de ce principe : on peut en effet vouloir une hypothèse moins contraignante sur l'équation que vérifie u, ou vouloir l'appliquer à des tenseurs plutôt qu'à des fonctions scalaires, mais l'idée est là : avec une ÉDP sur u, on déduit un contrôle dans le temps à partir d'un contrôle à l'origine.
Ces résultats justifient que l'on cherche à déterminer quelles équations vérifient les grandeurs géométriques associées à une métrique, comme la courbure. C'est ainsi que de l'équation vérifiée par la courbure scalaire R :
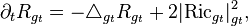
on, peut déduire que, sous le flot de Ricci, le minimum de la courbure scalaire croît.
Une version particulièrement forte de principe du maximum, le théorème de pincement de Hamilton et Ivey, valable uniquement en dimension trois, affirme que sous le flot de Ricci, les courbures sectionnelles restent contrôlées par la courbure scalaire. Ce théorème est fondamental dans l'étude du flot de Ricci, et son absence en dimension supérieure est une des causes de la rareté des résultats.
Le programme aujourd'hui
En trois articles retentissants (The entropy formula for the Ricci flow and its geometric applications, Ricci flow with surgery on three-manifolds et Finite extinction time for the solutions to the Ricci flow on certain three-manifolds), le mathématicien russe Grigori Perelman a exposé de nouvelles idées pour achever le programme de Hamilton. Il est à noter que Perelman n'a soumis aucun de ces articles à une revue mathématique et qu'ils sont disponibles sur le site web de diffusion de prépublications arXiv. Dans ces articles, Perelman prétend classer toutes les singularités (les κ-solutions) et faire traverser icelles au flot. Perelman affirme qu'ils constituent une preuve de la conjecture de Thurston et donc de celle de Poincaré.
N'ayant été soumis à aucune revue, ces articles n'ont d'autre raison d'être lus que leur extraordinaire portée. Leur extrême difficulté et technicité fait que leur lecture est affaire d'années de travail à temps plein pour des mathématiciens renommés. Depuis le Congrès international de mathématiques de 2006, et même si l'ICM ne cite pas explicitement la conjecture de Poincaré dans sa présentation de Perelman, l'idée que le programme de Hamilton est bel et bien achevé est de plus en plus répandue dans la communauté mathématique.

















































