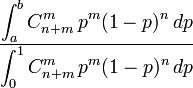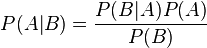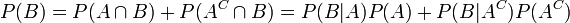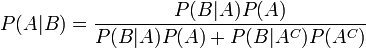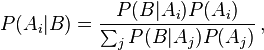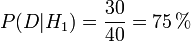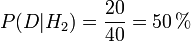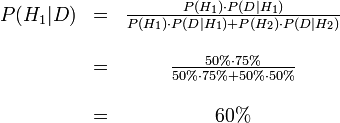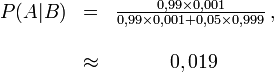Théorème de Bayes - Définition
Le théorème de Bayes est un résultat de base en théorie des probabilités, issu des travaux du révérend Thomas Bayes et retrouvé ensuite indépendamment par Laplace. Dans son unique article, Bayes cherchait à déterminer ce que l’on appellerait actuellement la distribution a posteriori de la probabilité p d’une loi binomiale. Ses travaux ont été édités et présentés à titre posthume (1763) par son ami Richard Price dans Un essai pour résoudre un problème dans la théorie des risques (An Essay towards solving a Problem in the Doctrine of Chances). Les résultats de Bayes ont été repris et étendus par le mathématicien français Laplace dans un essai de 1774, lequel n’était apparemment pas au fait du travail de Bayes.
Le résultat principal (la Proposition 9 de l’essai) obtenu par Bayes est le suivant : en considérant une distribution uniforme du paramètre binomial p et une observation m d'une loi binomiale
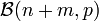
Ses résultats préliminaires, en particulier les propositions 3, 4 et 5 impliquent le résultat que l’on appelle théorème de Bayes (énoncé plus bas) mais il ne semble pas que Bayes se soit concentré ou ait insisté sur ce résultat.
Ce qui est " bayésien " (au sens actuel du mot) dans la Proposition 9, c’est que Bayes ait présenté cela comme une probabilité sur le paramètre p. Cela revient à dire qu’on peut déterminer, non seulement des probabilités à partir d’observations des issues d’une expérience, mais aussi les paramètres relatifs à ces probabilités. C’est le même type de calcul analytique qui permet de déterminer par inférence les deux. En revanche, si l’on en croit une interprétation fréquentiste, il ne peut pas exister de probabilité de distribution du paramètre p et par conséquent, on ne peut raisonner sur p qu’avec un raisonnement d’inférence non-probabiliste.
Le théorème de Bayes en Statistique
Le théorème de Bayes est utilisée dans l'inférence statistique pour mettre à jour ou actualiser les estimations d’une probabilité ou d'un paramètre quelconque, à partir des observations et des lois de probabilité de ces observations. Il y a une version discrète et continue du théorème.
- L’école bayésienne utilise les probabilités comme moyen de traduire numériquement un degré de connaissance (la théorie mathématique des probabilités n’oblige en effet nullement à associer celles-ci à des fréquences, qui n’en représentent qu’une application particulière résultant de la loi des grands nombres). Dans cette optique, le théorème de Bayes peut s’appliquer à toute proposition, quelle que soit la nature des variables et indépendamment de toute considération ontologique.
- Elle s'oppose à l’école fréquentiste, qui utilise les propriétés de long terme de la loi des observations et ne considère pas de loi sur les paramètres, inconnus mais fixés.
En théorie des probabilités, le théorème de Bayes énonce des probabilités conditionnelles : soit A et B deux évènements, le théorème de Bayes permet de déterminer la probabilité de A sachant B, si l’on connaît les probabilités
- de A,
- de B et
- de B sachant A.
Ce théorème élémentaire (originellement nommé de probabilité des causes) a des applications considérables.
Pour aboutir au théorème de Bayes, on part d’une des définitions de la probabilité conditionnelle :
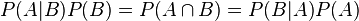
en notant
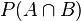
soit le théorème de Bayes.
Chaque terme du théorème de Bayes a une dénomination usuelle.
Le terme P(A) est la probabilité a priori de A. Elle est " antérieure " au sens qu’elle précède toute information sur B. P(A) est aussi appelée la probabilité marginale de A. Le terme P(A|B) est appelée la probabilité a posteriori de A sachant B (ou encore de A sous condition B) . Elle est " postérieure ", au sens qu’elle dépend directement de B. Le terme P(B|A), pour un B connu, est appelée la fonction de vraisemblance de A. De même, le terme P(B) est appelé la probabilité marginale ou a priori de B.
D’autres écritures du théorème de Bayes
On améliore parfois le théorème de Bayes en remarquant que
afin de réécrire le théorème ainsi :
où AC est le complémentaire de A. Plus généralement, si {Ai} est une partition de l’ensemble des possibles,
pour tout Ai de la partition.
Voyez aussi le théorème des probabilités totales.
La démarche d’I. J. Good
I. J. Good reprend une idée d’Alan Turing : les probabilités deviennent plus faciles à manier si au lieu de raisonner sur une probabilité p, on travaille sur une quantité construite de la façon suivante :
Ev(p) = ln (p/(1-p)) ou Ev(p) = log (p/(1-p))
qu’il nomme weight of evidence, terme auquel on peut donner différentes traductions : poids de témoignage, valeur de plausibilité, etc. Ce qui est intéressant à en retenir est ceci :
- Une evidence peut varier de moins l’infini à plus l’infini.
- On travaille souvent par commodité en décibels (dB), 10 log10 (p/(1-p))
- L’observation d’un phénomène se traduit par une variation d’evidence qui constitue une translation d’evidence, la valeur de cette translation ne dépendant pas des probabilités a priori de l’utilisateur. Une observation apporte donc une information objective qui est la même pour tous les observateurs, ce que la loi de Bayes ne mettait pas en... évidence.
En calculs de fiabilité, où il faut manier des probabilités très grandes (1-ε) et très petites (ε), travailler en terme d’evidences permet une visualisation bien plus claire classes de sécurité : une évidence de -70dB correspond à une probabilité de 10-7, etc. On peut également travailler en gardant en toutes circonstances le même nombre de décimales et sans manipuler d’exposants, ce qui améliore la lisibilité des calculs.
Théorème de Bayes pour des densités de probabilité
Il existe aussi une version du théorème pour les distributions continues qui se déduit simplement de la densité jointe des observations et des paramètres, produit de la vraisemblance par la densité a priori sur les paramètres, par application de la définition des lois et des densités conditionnelles.
La forme continue du théorème de Bayes peut aussi s'interpréter comme indiquant que la distribution a posteriori s’obtient en multipliant la distribution a priori, par la vraisemblance, et en effectuant une normalisation (du fait qu'il s'agit d'une densité de probabilité). En calcul bayésien, on prend donc l'habitude de travailler avec des signes de proportionalité plutôt que des égalités pour diminuer la complexité des expressions puisque les constantes manquantes se retrouvent par intégration (en principe). Les techniques de simulation de type Monte Carlo et MCMC n'utilisent d'ailleurs pas ces constantes de normalisation.
L’exemple le plus connu est le suivant : si l’on observe K numéros de séries d’appareils, que le plus grand est S, et qu’on les suppose numérotés à partir de 1, quelle est la meilleure estimation du nombre N d’appareils existants ? On démontre que le meilleur estimateur simple est N = S x (K-1)/(K-2), et surtout que la précision de cette estimation croît très vite, même avec de petites valeurs de K.
Autre exemple possible : supposons qu’une proportion p inconnue d’électeurs vote " Oui " avec :
![p \in [0,1]](https://static.techno-science.net/illustration/Definitions/autres/5/550abf67410399d394e58560a62f657a_9c5265e725cf00b65260a295ec86439b.png)
- L(p) = [constante] px (1 − p)n−x.
En multipliant cela par la fonction de densité de probabilité a priori de p et en normalisant, on calcule la distribution de probabilité a posteriori de p, ce qui injecte l'information des nouvelles données du sondage. Ainsi, si la probabilité a-priori de p est uniforme sur l'intervalle [0,1], alors la probabilité a-posteriori aura la forme d'une fonction Beta.
- f(p|x) = [constante] px (1 − p)n−x
la constante étant différente de celle de la fonction de vraisemblance.
La fonction Beta se retrouve avec une grande régularité dans ces questions d’estimation. Le calcul de la variation d’entropie entre l’ancienne et la nouvelle distribution permet de quantifier exactement, en bits, l’information obtenue.
Inférence bayésienne
Les règles de la théorie mathématique des probabilités s’appliquent à des probabilités en tant que telles, pas uniquement à leur application en tant que fréquences relatives d’évènements aléatoires. On peut décider de les appliquer à des degrés de croyance en certaines propositions. Ces degrés de croyance s’affinent au regard d’expériences en appliquant le théorème de Bayes.
Le Théorème de Cox-Jaynes justifie aujourd’hui très bien cette approche, qui n’eut longtemps que des fondements intuitifs et empiriques.
Exemples
De quelle urne vient la boule ?
À titre d’exemple, imaginons deux urnes remplies de boules. La première contient dix (10) boules noires et trente (30) blanches ; la seconde en a vingt (20) de chaque. On tire sans préférence particulière dans une des urnes au hasard et dans cette urne, on tire une boule au hasard. La boule est blanche. Quelle est la probabilité qu'on tire dans la première urne cette boule sachant qu'elle est blanche?
Intuitivement, on comprend bien que c’est plus vraisemblable que le contraire, donc que la probabilité devrait être plus que 50 %. La réponse exacte vient du théorème de Bayes.
Soit H1 l’hypothèse " On tire dans la première urne. " et H2 l’hypothèse " On tire dans la seconde urne. ". Comme on tire sans préférence particulière, P(H1) = P(H2) ; de plus, comme on a certainement tiré dans une des deux urnes, la somme des deux probabilités vaut 1 : chaque vaut 50 %.
Notons 'D' l’information donnée " On tire une boule blanche. " Comme on tire une boule au hasard dans une des urnes, la probabilité de D sachant/sous l’hypothèse H1 vaut :
De même si l’on considère H2,
La formule de Bayes dans le cas discret nous donne donc.
Avant que l’on regarde la couleur de la boule, la probabilité d’avoir choisi la première urne est une probabilité a-priori, P(H1) soit 50 %. Après avoir regardé la boule, on révise notre jugement et on considère P(H1|D), soit 60 %.
Pronostics contradictoires
- Une station météo A prévoit du beau temps pour demain.
- Une autre, B, prévoit au contraire de la pluie.
- On sait que dans le passé A s’est trompée 25% du temps dans ses prévisions, et B 30% du temps.
- On sait aussi qu’en moyenne 40% des jours sont de beau temps et 60% de pluie.
Qui croire, et avec quelle probabilité?
Cette approche bayésienne est utilisée par les centres anti-poison pour détecter le plus vite possible et avec le maximum de précision le type d’empoisonnement dont souffre probablement un patient.
Aspects sociaux, juridiques et politiques
Un problème régulièrement soulevé par l’approche bayésienne est le suivant : si une probabilité de comportement (délinquance, par exemple) est fortement dépendante de certains facteurs sociaux, culturels ou héréditaires, alors :
- d’un côté, on peut se demander si cela ne suppose pas une partielle réduction de responsabilité, morale à défaut de juridique des délinquants. Ou, ce qui revient au même, à une augmentation de responsabilité de la société, qui n’a pas su ou pas pu neutraliser ces facteurs.
- d’un autre côté, on peut souhaiter utiliser cette information pour orienter au mieux une politique de prévention, et il faut voir si l’intérêt public ou la morale s’accommoderont de cette discrimination de facto des citoyens (fût-elle positive).
Ces problèmes sont abordés dans le film Minority Report.
" Faux positifs " médicaux
Commençons par poser un problème (trop) simplifié, qui n’aura d’autre mérite que d’introduire le problème réel.
Le problème " simplifié "
- Le test médical d’une maladie rare est considéré comme fiable à 99%.
- Cette maladie touche une personne sur 100 000 dans la population.
- Vous effectuez le test. Il se révèle positif.
Pas de panique. Sous la forme donnée, ce problème simplifié (on pourrait dire caricaturé) nous indique que sur un million de personnes, dix mille (1%) seront considérées comme atteintes alors que 10 seulement (une sur 100 000) sont atteintes de la maladie. Ce test fiable à 99% donne, dans le cas où il est positif, heureusement 999 fausses alertes sur 1000.
Cela ayant eu juste pour but de fixer les idées, passons au cas réel.
Le problème réel
Les faux positifs sont une difficulté inhérente à tous les tests : aucun test n’est parfait. Parfois, le résultat sera positif à tort, ce que l’on nomme parfois risque du premier ordre ou risque alpha.
Par exemple, quand on teste une personne pour savoir si elle est infectée par une maladie, il y a un risque généralement infime que le résultat soit positif alors que le patient n’a pas contracté la maladie. Le problème alors n’est pas de mesurer ce risque dans l’absolu (avant de procéder au test), il faut encore déterminer la probabilité qu’un test positif le soit à tort. Nous allons montrer comment, dans le cas d’une maladie très rare, le même test par ailleurs très fiable peut aboutir à une nette majorité de positifs illégitimes.
Imaginons un test extrêmement fiable :
- si un patient a contracté la maladie, le test le fait remarquer, c’est-à-dire est positif, presque systématiquement, 99 % des fois, soit avec une probabilité 0,99 ;
- si un patient est sain, le test est correct, c’est-à-dire négatif dans 95 % des cas, soit avec une probabilité 0,95 ;
Imaginons que la maladie ne touche qu’une personne sur mille, soit avec une probabilité 0,001. Cela peut paraître peu mais dans le cas d’une maladie mortelle, c’est considérable. Nous avons toutes les informations nécessaires pour déterminer la probabilité qu’un test soit positif à tort.
Désignons par A l’évènement " Le patient a contracté la maladie " et par B l’évènement " Le test est positif ". La seconde forme du théorème de Bayes dans le cas discret donne alors :
Sachant que le test est positif, la probabilité que le patient soit sain vaut donc environ : (1 − 0,019) = 0,981. Du fait du très petit nombre de malades,
- pratiquement tous les malades présentent un test positif, mais
- pratiquement aussi, tous les tests positifs désignent des porteurs sains.
Si le traitement est très lourd, coûteux ou dangereux pour un patient sain, il peut être alors inopportun de traiter tous les patients positifs sans risque ou test complémentaire (qui sera sans doute plus précis et plus coûteux, le premier test n’ayant servi qu’à écarter les cas les plus évidents).
On a tout de même réussi avec le premier test à isoler une population vingt fois moindre qui contient pratiquement tous les malades. En procédant à d’autres tests, on peut espérer améliorer la fiabilité du test. Le théorème de Bayes nous montre que dans le cas d’une probabilité faible de malades, le risque d’être déclaré positif à tort a un impact très fort sur la fiabilité.