Théorème de complétude de Gödel - Définition
Le théorème de complétude du calcul des prédicats du premier ordre a été prouvé par Kurt Gödel (1929, thèse de doctorat, Sur la complétude du calcul logique). Il affirme que le calcul des prédicats est complet au sens où on connaît des listes finies et complètes de tous ses principes. Autrement dit toute démonstration mathématique peut en principe se formaliser en calcul des prédicats.
Nous allons donner plusieurs définitions équivalentes de cette notion de complétude.
Diverses formulations équivalentes du théorème de complétude
On peut donner un nombre fini d’axiomes, de schémas d’axiomes ou de règles de déduction tel que toutes les preuves logiquement valides formulées avec la grammaire du calcul des prédicats du premier ordre soient obtenues à partir de ces principes.
La notion de validité logique d’une preuve est précisée par la théorie des modèles. Une règle de déduction est valide lorsque tout modèle de ses prémisses est aussi un modèle de sa conclusion. Un axiome logique est valide lorsqu’il est vrai dans tous les modèles. Un schéma d’axiomes est un principe logique valide lorsque tous les axiomes produits par ce schéma sont des axiomes logiques valides. Un système de principes logiques est valide ou correct lorsque ses axiomes, ses schémas d’axiomes et ses règles de déduction sont valides. Une preuve est logiquement valide lorsqu’elle peut être formalisée dans le cadre d’un système logique valide.
Nous allons prouver que la liste des quinze règles de déduction naturelle est un système complet des principes de la logique du premier ordre. Ce théorème est équivalent à celui de Gödel. Mais la preuve de Gödel est basée sur une autre formulation des principes logiques, celle des Principia Mathematica de Whitehead et Russell.
Pour cela, donnons quelques définitions :
- celles relatives à l'utilisation de modèles (du premier ordre) : satisfaisabilité et falsifiabilité, loi logique et contradiction logique, conséquence logique, prouvabilité
- Une formule du calcul des prédicats est satisfaisable ou possiblement vraie lorsqu’elle est vraie dans au moins un modèle. Elle est universellement valide, ou est une loi logique, lorsqu’elle est vraie dans tous les modèles. Si p est une loi logique, on note
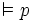
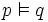
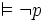
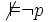
- celles relatives aux systèmes de déduction (pour le calcul des prédicats du premier ordre) : cohérence et incohérence, prouvabilité.
- Si p est une formule du calcul des prédicats, p est prouvable dans un système de déduction pour la logique L, lorsqu’il existe une preuve de p dans L, au sens où les règles de déduction de L suffisent pour déduire p en un nombre fini d'étapes dans L, ce qu'on note
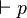
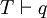
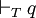
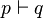
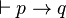
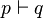
Notons
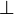
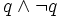
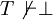
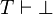
Un système de déduction correct se doit de ne pouvoir prouver, à partir de formules vraies, que des propositions vraies, en particulier, on attend que, si
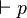
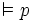
Le théorème de complétude se préoccupe de la réciproque. Cela signifie que le système de déduction L se doit d'être suffisamment complet (d'où le nom du théorème) de façon à pouvoir prouver toute loi logique, i.e. toute formule vraie dans tout modèle. Le théorème de complétude peut être énoncé sous la forme suivante (exprimée pour une formule, une forme plus forte du théorème de complétude s'écrit pour un nombre éventuellement infi de formules) :
Il existe des systèmes de déduction logiques valides L qui satisfont aux conditions équivalentes suivantes :
- pour toutes formules p et q (du calcul des prédicats du premier ordre), si q est une conséquence logique de p alors q est prouvable à partir de p dans L. Si
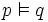
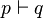
- Pour toute formule p, si p est une loi logique alors p est prouvable. Si
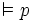
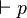
- Pour toute formule p, si p est une contradiction logique alors (non p) est prouvable. Si
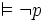
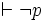
- Pour toute formule p, si p est une contradiction logique alors p est incohérente dans L. Si
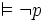
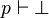
- Pour toute formule p, si p est cohérente dans L alors p est satisfaisable. Si
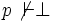
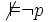
On peut enfin remarquer qu'un ensemble défini par induction avec un nombre fini de principes (axiomes, schémas d'axiomes et règles de déduction) est énumérable. Autrement dit, toutes les théories axiomatiques usuelles sont des ensembles énumérables. Le théorème de complétude dit qu'il existe des théories axiomatiques complètes de la logique du premier ordre.
Il en résulte que l'ensemble des lois logiques est énumérable.
Cela permet de relier ce théorème de complétude à la théorie de l'indécidabilité, parce qu'on peut prouver que l'ensemble des lois logiques est indécidable. Autrement dit, l'ensemble des formules falsifiables n'est pas énumérable, ou, de façon équivalente, l'ensemble des formules satisfaisables n'est pas énumérable (voir également le théorème d'incomplétude et le théorème de Tarski).
La validité du calcul des prédicats du premier ordre
Un système de déduction pour le calcul des prédicats étant choisi, on montre que si une formule c est déductible, avec les règles de ce système à partir d'un ensemble de formules h (
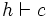
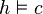
La preuve se fait par récurrence sur la taille des preuves, taille que l'on définit pour chaque système de déduction. Il s'agit alors de vérifier que chaque axiome logique est valide, et que chaque règle conserve la validité. La preuve est triviale, mais fastidieuse à rédiger entièrement.
Précisons un peu le cas de la déduction naturelle : il est plus commode d'utiliser une formulation de celle-ci en termes de séquents (ayant un nombre fini de prémisses et une conclusion).
Il faudrait manipuler des formules avec variables libres. Pour simplifier (l'idée est la même) faisons comme si nous étions en calcul propositionnel, c’est-à-dire que toutes les formules sont closes, il n'y a pas de quantificateurs. Un séquent est valide lorsque tout modèle de ses prémisses est aussi un modèle de sa conclusion.
Un séquent est prouvable s'il est ou bien un axiome, ou bien déduit des axiomes par un nombre fini d'applications des règles de la déduction naturelle. Les axiomes sont ici tous les séquents de la forme
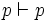
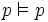
Par exemple, supposons que l'on ait prouvé
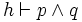
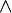
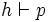
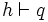
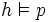
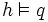
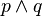
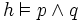
En appliquant la même vérification à tous les séquents, on prouve que, si
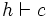
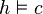
Pour en déduire que les formules prouvables (
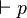
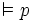
L'existence d'un modèle sous l'hypothèse de cohérence
Nous allons prouver le théorème de complétude sous la forme suivante.
- Si une formule est cohérente alors elle est satisfaisable. Si
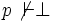
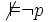
En fait nous prouverons une version renforcée de ce théorème.
- Si un ensemble d'axiomes est cohérent alors il est satisfaisable.
Un ensemble d'axiomes est cohérent lorsqu'aucune contradiction n'est prouvable à partir d'un nombre quelconque, fini, de ces axiomes. Il est satisfaisable lorsqu'il y a un modèle dans lequel les axiomes sont tous vrais. Cette version renforcée du théorème est utile en particulier pour énoncer le paradoxe de Skolem, parce qu’elle permet d’appliquer le théorème de complétude à des systèmes infinis d’axiomes.
Commençons par montrer comment remplacer un système d’axiomes du calcul des prédicats par un système équivalent d’axiomes du calcul des propositions. Pour cela, on commence par mettre chaque axiome sous une forme prénexe.
Une formule du calcul des prédicats est toujours équivalente à une formule mise sous forme prénexe, c’est-à-dire une formule dans laquelle tous les quantificateurs universels et existentiels sont placés au début et non à l'intérieur des sous-formules. On peut toujours prouver qu'une formule est équivalente à une formule prénexe avec les règles de déduction suivante :
- de
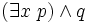
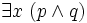
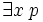
- de
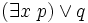
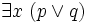
- deux autres règles semblables pour le quantificateur universel
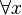
- de
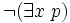
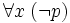
- de
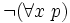
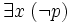
Toutes ces règles sont des règles dérivées dans le système de déduction naturelle et elles font toutes passer d'une prémisse à une conclusion équivalente. Par itération elles fournissent une formule prénexe équivalente à la formule initiale.
De la forme prénexe d'un axiome, on passe à sa forme de Skolem en introduisant de nouveaux opérateurs fondamentaux, autant qu’il en faut pour faire disparaître tous les quantificateurs existentiels dans les axiomes. Par exemple, l’axiome prénexe
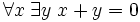
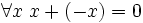
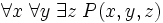
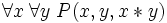
On construit alors un univers, un domaine des êtres nommés. Les noms des objets de base sont ceux qui sont mentionnés dans les axiomes. S’il n’y en a pas, on en introduit un, qu’on peut appeler comme on veut, 0 par exemple.
L’ensemble des noms d’objet est celui obtenu par induction à partir des noms des objets de base et des noms de tous les opérateurs mentionnés dans les axiomes d’origine ou introduits par la méthode ci-dessus exposée. L’univers U est l’ensemble de tous les êtres ainsi nommés.
Chaque forme de Skolem d'un axiome peut être conçue comme un schéma d’axiomes à l'intérieur du calcul des propositions. On supprime tous les quantificateurs universels et on remplace toutes les variables alors libres par des noms d’objet. À chaque axiome de départ on associe ainsi un ensemble infini de formules du calcul des propositions. La réunion de toutes ces formules associées à tous les axiomes de départ, est le nouveau système d’axiomes, non quantifiés, équivalent au système d’origine.
Montrons maintenant que si un sous-ensemble fini du système d'axiomes non-quantifiés est incohérent alors le système d'axiomes d'origine est lui aussi incohérent. Soit C une conjonction incohérente d'axiomes non-quantifiés. Soit C' la formule obtenue à partir de C en remplaçant toutes ses constantes par des variables distinctes, de telle façon que C ne contienne plus d'opérateurs d'objet, et en quantifiant existentiellement sur toutes ces variables. Comme C est incohérente, C' l'est aussi. Mais C' peut être prouvée à partir d'un nombre fini des axiomes d'origine, qui sont donc eux aussi incohérents.
Si un système d'axiomes est cohérent tous les sous-ensembles finis du système d'axiomes non quantifiés sont également cohérents. D'après le théorème de complétude du calcul des propositions, ils sont donc tous satisfaisables. D'après le théorème de compacité, le système - infini - d'axiomes non quantifiés est lui aussi satisfaisable. Comme un modèle du système d'axiomes non-quantifiés est également un modèle du système d'origine, on a prouvé l'existence d'un modèle pour tout système cohérent d'axiomes.
Le théorème de Löwenheim et le paradoxe de Skolem
L'ensemble de noms à partir duquel un modèle est construit dans la preuve ci-dessus est dénombrable. On a donc prouvé également le théorème de Löwenheim-Skolem (prouvé en 1915 par Leopold Löwenheim et complété ensuite pour les systèmes infinis d'axiomes par Thoralf Skolem.
- Si un système d'axiomes fini ou infini dénombrable a un modèle alors il a un modèle dénombrable.
On voit que la preuve repose sur le fait que dans un langage dénombrable (langage au sens large : les formules du langage de la théorie en font partie) on ne peut traiter que d'une collection dénombrable d'objets.
Appliqué à la théorie des ensembles, ce théorème semble paradoxal. La théorie des ensembles de Zermelo et ses extensions comme la théorie ZFC sont développées dans un langage dénombrable, qui utilise un ensemble infini dénombrable d'axiomes. Donc cette théorie et ces extensions ont un modèle dénombrable.
En utilisant l'axiome de l'infini et l'axiome de l'ensemble des parties, on montre l'existence de
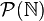
Le paradoxe n'est qu'apparent ; il disparait dès que l'on pense que le modèle dénombrable dont on a montré l'existence ne s'identifie pas avec l'univers dans lequel on a travaillé pour montrer celle-ci. En particulier "dénombrable" ne signifie plus la même chose à l'intérieur de ce modèle dénombrable.
En effet on sait que dans un modèle (ou univers) de la théorie des ensembles, dont les objets sont des ensembles, il existe des collections d'objets (des ensembles au sens intuitif), que l'on peut éventuellement définir par une formule, par exemple les objets qui ne s'appartiennent pas à eux-mêmes (voir paradoxe de Russell), mais qui ne sont pas des ensembles : on ne peut trouver d'objet du modèle auquel appartiennent les objets d'une de ces collections (et seulement ceux-ci). Or dire qu'un ensemble est dénombrable, c'est dire qu'il existe une fonction, c’est-à-dire un ensemble de couples, qui est une bijection de
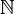
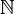
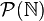
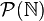
On peut discuter de ce que veut dire "au sens intuitif" dans l'explication ci-dessus : c'est une commodité d'expression. Tout ceci se formalise dans une théorie des ensembles (plus forte que celle que l'on étudie). Dit sémantiquement, dans l'univers de la théorie des ensembles dans lequel on travaille, on a défini un modèle, un objet de cet univers, qui est un modèle dénombrable (au sens de cet univers) de la théorie de Zermelo, mais à l'intérieur duquel, au sens maintenant du modèle que l'on a construit, il existe des ensembles non-dénombrables.
Notes
- ↑ Remarquons que cette collection, contrairement à la collection des ensembles qui ne s'appartiennent pas à eux-mêmes, n'est même pas une classe, c’est-à-dire définie par une formule, puisque, par compréhension, ce serait un ensemble.

















































