Équation du temps - Définition
La liste des auteurs de cet article est disponible ici.
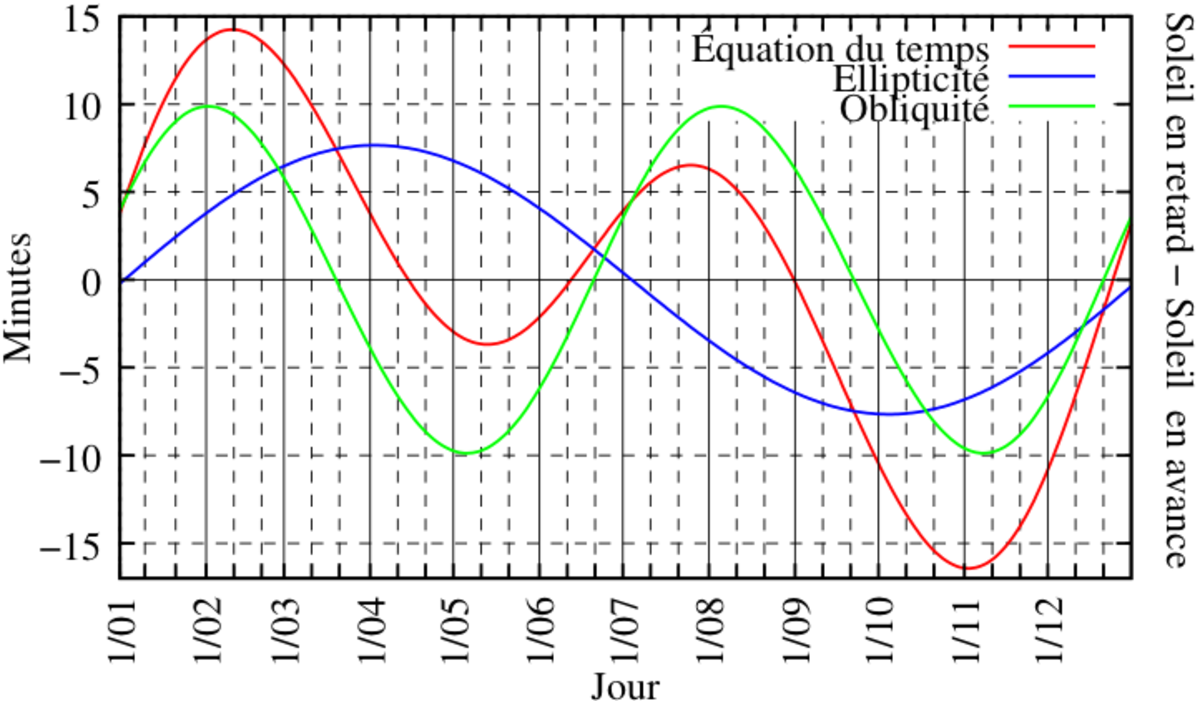
Evolution annuelle de l'équation du temps
L'évolution de l’équation du temps sur une année complète est représentée par la courbe rouge sur la figure ci-contre. En première approximation, sa forme s'analyse comme résultant de la superposition de deux sinusoïdes :
- En bleu sur le diagramme : une sinusoïde de période égale à un an, d'amplitude égale à 7,66 minutes et s'annulant aux passages de la Terre aux apsides : périgée le 3 janvier et apogée début juillet. Cette composante reflète l'excentricité de l'orbite terrestre.
- En vert sur le diagramme, une sinusoïde de période égale à une demi-année, d'amplitude 9,87 minutes et s'annulant aux solstices et aux équinoxes. Cette composante résulte de l'obliquité de l'écliptique sur l'équateur.
L'équation du temps, en rouge, s'annule quatre fois par an, vers le 15 avril, le 13 juin, le 1er septembre et le 25 décembre. Son maximum, atteint vers le 11 février, vaut 14 min 15 s, et son minimum, atteint vers le 3 novembre, vaut − 16 min 25 s.
Analemme
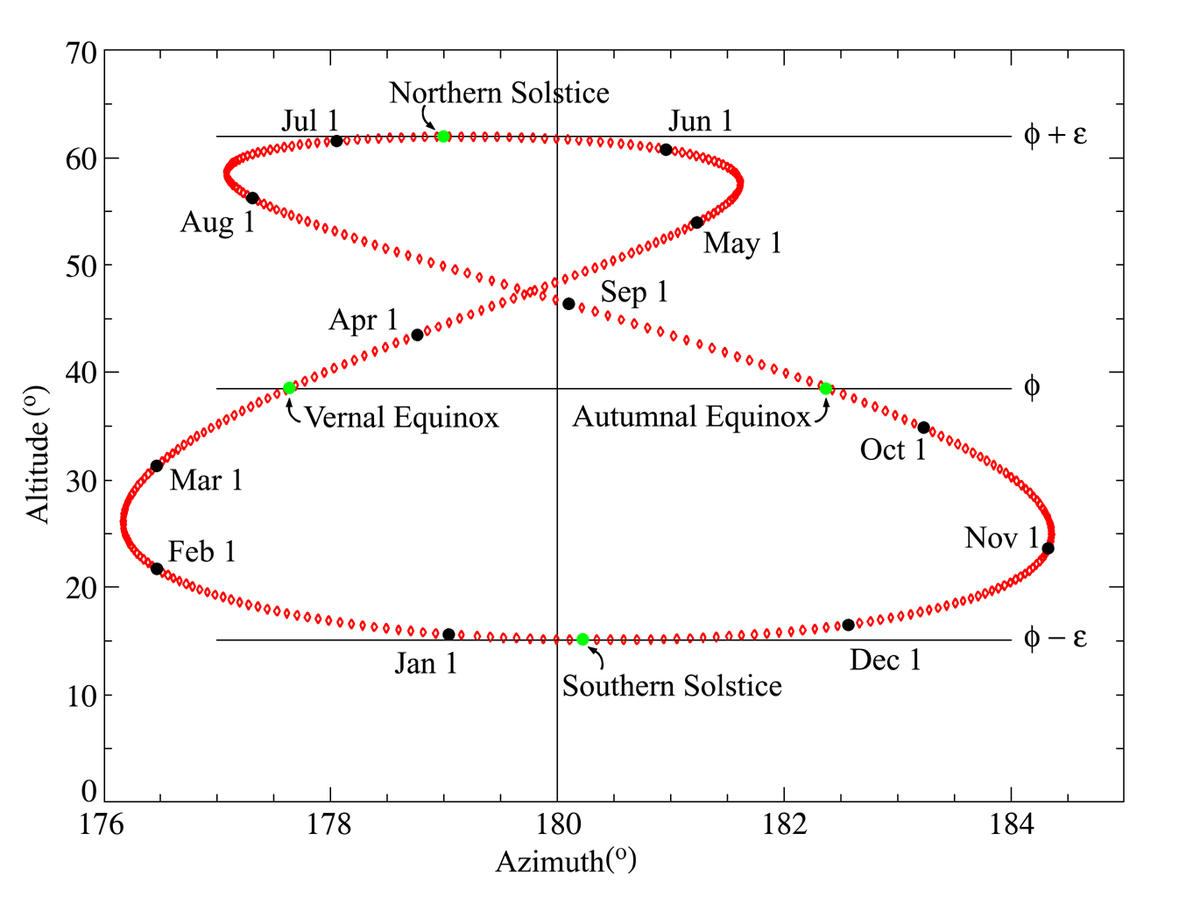
Latitude 51,4791° nord, colatitude = 38,5209°, longitude 0°.
L'évolution annuelle de l'équation du temps, en un lieu donné, peut être visualisée à l'aide d'une courbe appelée analemme ou courbe en 8, définie comme suit : chaque point de cette courbe représente une position du soleil (vrai) lorsqu'il est 12 h pour le soleil moyen, c'est-à-dire lorsque ce dernier passe au centre du diagramme. Les axes sont les suivants, avec des échelles différentes, de façon à mieux mettre en évidence la légère asymétrie de la courbe :
- L'axe horizontal représente l'azimut en degrés (180° correspond au sud). L'équation du temps se lit le long de cet axe, donc comme l'écart horizontal par rapport à la ligne 180°. Avec la convention de signe adoptée, elle est positive à gauche de la ligne 180°. La correspondance entre l'angle et le temps est 360° = 24 h, donc 1° = 4 minutes.
- L'axe vertical représente la hauteur du soleil au-dessus de l'horizon, liée aux variations de sa déclinaison.
- Le soleil moyen, midi moyen, se trouve au centre du diagramme (azimut = 180°, hauteur = 90° - latitude du lieu)
Sur l'exemple ci-contre, le premier jour de chaque mois est affiché en noir, et les positions des solstices et équinoxes sont affichées en vert. On lit par exemple :
- le 3 novembre, avance maximale du soleil vrai sur le soleil moyen, et l'équation du temps, qui est négative, vaut - 16 min 23 sec ;
- le 12 février, le retard est maximal, et l'équation du temps, qui est positive, vaut + 14 min 20 sec ;
- au solstice d'hiver, vers le 21 décembre, la hauteur du soleil est minimale et vaut 15,08° (hauteur au solstice d'hiver = colatitude du lieu - obliquité de l'écliptique = 38,52° - 23,44°) ;
- au solstice d'été, vers le 21 juin, la hauteur est maximale et vaut 61,96° (hauteur au solstice d'été = colatitude du lieu + obliquité de l'écliptique = 38,52° + 23,44°) ;
- aux équinoxes, le soleil passe dans le plan de l'équateur et a, à ce moment-là, la même hauteur que le soleil moyen, égale à la colatitude du lieu
Certains cadrans solaires sont munis d'un analemme. Ils peuvent même donner directement le temps moyen, soit parce que les droites horaires sont transformées en courbes corrigées de l'équation du temps, soit parce que le gnomon a reçu une forme tenant compte de cette correction. Dans les deux cas, il faut tenir compte de la période de l'année ou disposer de deux cadrans.
Homonymie
Il ne faut pas confondre cet analemme avec la figure du même nom, qui lui est historiquement bien antérieure, et qui servait à tracer des cadrans solaires ou établir géométriquement la hauteur du soleil. Elle résultait de la projection de la sphère céleste sur le plan méridien.
Variation de cette évolution au cours du temps
La forme de la courbe « équation du temps », c'est-à-dire la valeur des extrema et les instants où on les observe, ainsi que les instants où la courbe s'annule, évoluent très lentement au cours des années pour au moins deux raisons :
- la Terre dans son mouvement autour du Soleil subit l'influence des autres planètes du système solaire, ce qui entraîne une variation de l'excentricité de son orbite, ainsi qu'une lente rotation de la ligne joignant le périhélie à l'aphélie de l'orbite, appelée ligne des apsides.
- la Terre, dans sa rotation sur elle-même, subit l'influence du couple (Lune, Soleil), ce qui entraîne une variation de son obliquité en inclinaison et direction ; ces phénomènes sont connus et décrits sous le nom de nutation en longitude, nutation en obliquité et précession des équinoxes.
Ces évolutions provoquent notamment un glissement relatif des dates des passages aux apsides par rapport à celles des solstices et des équinoxes, qui sont fixes par construction de l'année tropique. Sur une durée de 70 siècles, de l'an - 2000 à + 5000, les extrema sont définis par le tableau suivant :
| Année | Premier maximum | Premier minimum | Deuxième maximum | Deuxième minimum |
|---|---|---|---|---|
| - 2000 | + 18 min 33 s, 31 janvier | - 12 min 45 s, 20 mai | + 2 min 06 s, 10 août | - 9 min 30 s, 26 octobre |
| - 1000 | + 18 min 18 s, 3 février | - 10 min 14 s, 21 mai | + 2 min 06 s, 6 août | - 11 min 45 s, 27 octobre |
| 0 | + 17 min 27 s, 6 février | - 7 min 44 s, 20 mai | + 2 min 57 s, 1er août | - 13 min 45 s, 29 octobre |
| + 1000 | + 16 min 04 s, 9 février | - 5 min 27 s, 18 mai | + 4 min 30 s, 29 juillet | - 15 min 20 s, 1er novembre |
| + 2000 | + 14 min 15 s, 11 février | - 3 min 41 s, 14 mai | + 6 min 30 s, 26 juillet | - 16 min 25 s, 3 novembre |
| + 3000 | + 12 min 08 s, 14 février | - 2 min 37 s, 10 mai | + 8 min 41 s, 25 juillet | - 16 min 57 s, 6 novembre |
| + 4000 | + 9 min 52 s, 15 février | - 2 min 24 s, 6 mai | + 10 min 48 s, 25 juillet | - 16 min 54 s, 9 novembre |
| + 5000 | + 7 min 38 s, 15 février | - 3 min 00 s, 3 mai | + 12 min 38 s, 26 juillet | - 16 min 17 s, 12 novembre |