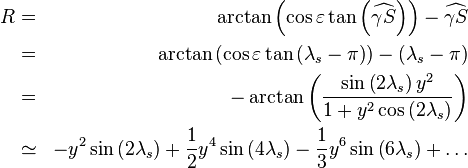Équation du temps - Définition

Étude détaillée

Influence de l'ellipticité de l'orbite de la terre

• Calcul de l'anomalie moyenne

avec J₂₀₀₀ = 2451545. J est le jour julien de la date considérée. En première approximation, (J − J₂₀₀₀) peut être remplacé par le numéro d du jour dans l'année (d = 1 le premier janvier).

• Contribution de l'ellipticité de la trajectoire : c'est l'équation du centre en radian où e = 0,01671 représente l'excentricité de la trajectoire de la Terre autour du Soleil.

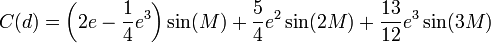
Application numérique :

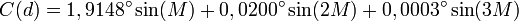
Influence de l'obliquité de la terre

• Calcul de la longitude écliptique

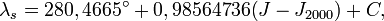
la petite différence de période entre λ_s et M est est due à la précession des équinoxes

• Contribution de l'obliquité de la Terre : c'est la réduction à l'équateur (en radian) où y = tan(ε / 2) ; ε = 23,43929^o représente l'inclinaison de l'axe de la Terre par rapport au plan de l'écliptique.

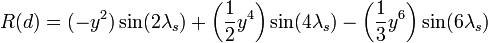
Application numérique :

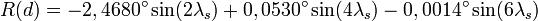
Équation du temps

Équation du temps en degrés :

E(d) = C(d) + R(d), où C et R sont exprimés en degrés.

Équation du temps en minutes :

, où E est exprimé en degrés.

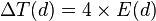
Explications et démonstration de la formule

La figure 1 montre la Terre T qui tourne sur elle même et qui tourne autour du Soleil S en un an dans le plan de l'écliptique. La situation présentée correspond à l'automne. Le point P est le périhélie, atteint au début du mois de janvier. L'angle θ s'appelle anomalie vraie. L'axe γ, appelé axe vernal ou point vernal, est l'intersection du plan de l'écliptique avec le plan équatorial. Il sert d'origine pour mesurer la longitude écliptique λ_s.

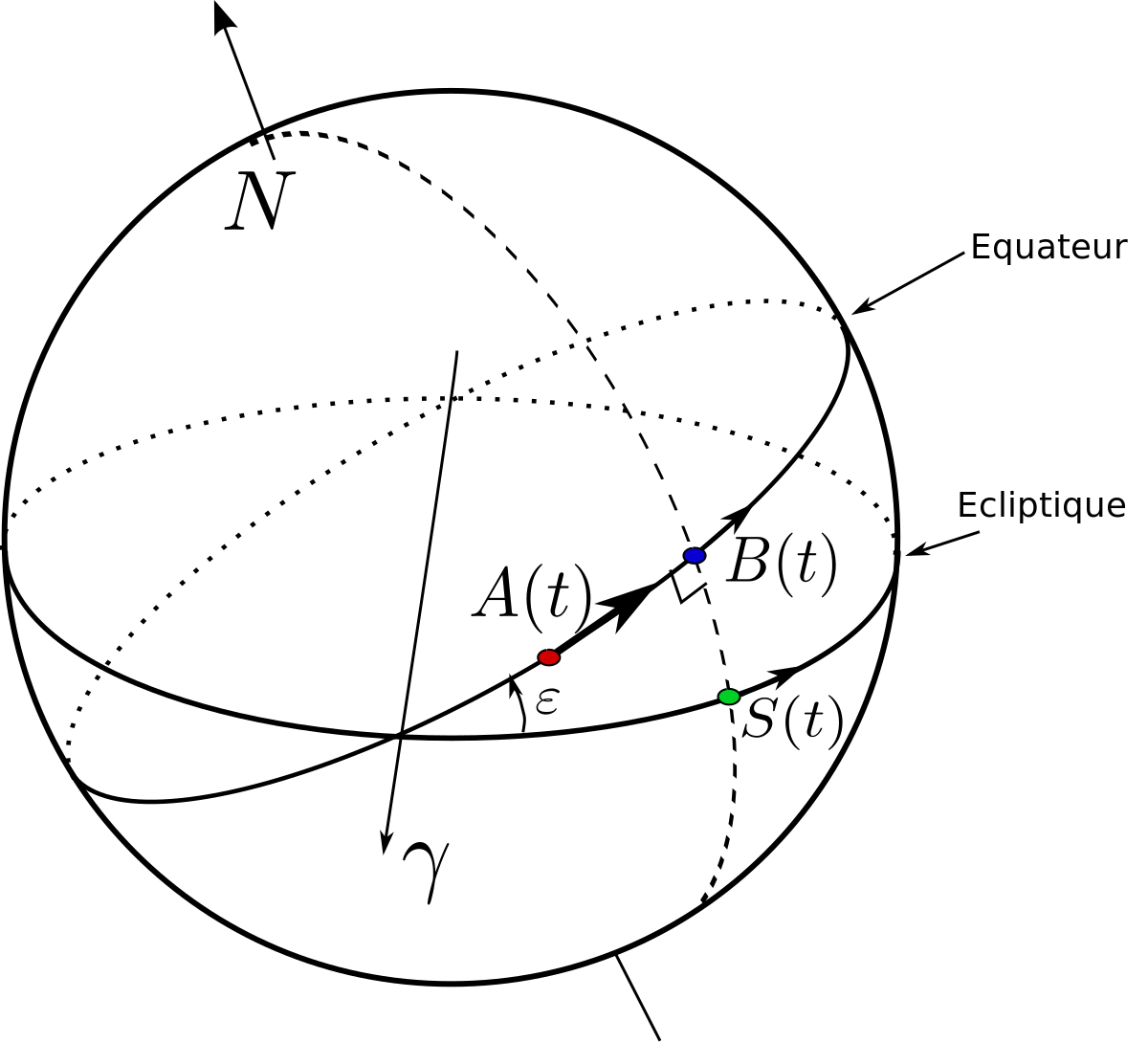
La figure 2 représente la Terre dans un repère fixe par rapport aux étoiles. L'obliquité est l'angle entre le plan de l'écliptique et le plan de l'équateur.

Appelons t le temps qui s'écoule. Considérons un point fixé sur Terre et positionné sur l'équateur. Il fait donc un tour en un jour sidéral de façon régulière.

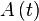
Partant du centre de la terre, le point est situé en direction du Soleil. Il se situe donc sur le cercle de l'écliptique. Le point fait un tour en une année sidérale.

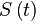
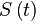
Comme l'orbite terrestre est elliptique et d'après les lois de Kepler, ne tourne pas de façon régulière. Considérons le méridien passant par et appelons l'intersection de ce méridien avec l'équateur. Remarquons qu'il est midi solaire au point A lorsque le point traverse ce méridien (i.e. lorsque les points

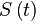
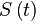
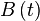
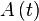
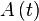
et coïncident). Remarquons aussi qu'un jour solaire vrai est la durée qui sépare deux croisements de et . Plus généralement l'heure solaire vraie est l'angle entre et  :

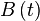
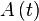
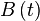
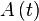
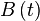
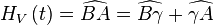
H_V est l'heure qu'indiquerait un cadran solaire.

Pour définir l'heure solaire moyenne, il faut se référer à des mouvements réguliers (moyennés). Nous avons vu que le point a un mouvement régulier. Ce n'est pas le cas du point , ni même du point . À la place de on considère un point virtuel sur l'écliptique qui a un mouvement régulier et de même période (on verra que est directement relié à l'anomalie moyenne ).

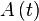
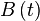
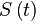
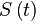
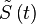
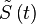
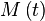
Par conséquent l'heure solaire moyenne est :

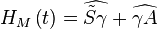
Par définition l'équation du temps est la différence :

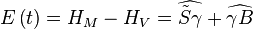
Or une relation de trigonométrie donne :

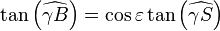
En effet, projetons à partir du centre de la terre le triangle sphérique SγB sur le plan tangent à la terre au point vernal γ. Il devient un triangle rectangle d'angle au sommet γ et de côté adjacent et d'hypothénuse . On déduit la relation .

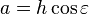
On déduit :

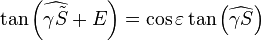
et l'expression de l'équation du temps :

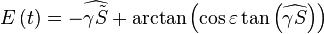
Remarques

• Dans cette dernière équation tout est connu. D'une part, d'après la figure 1 il apparaît que l'angle est reliée à la longitude écliptique λ_s par

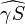
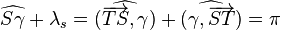
et λ_s elle même est reliée à l'anomalie vraie par où est la longitude du périhélie. Donc

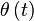
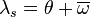
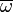
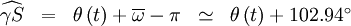
De même est relié à l'anomalie moyenne par

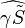
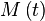
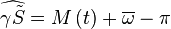
• Traditionnellement on décompose E(t) de la façon suivante :

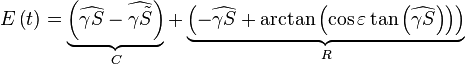
Le premier terme, C, est appelé « contribution de l'ellipticité » ou équation du centre. On a : . C est dû à l'ellipticité de l'orbite terrestre. Dans un modèle où la Terre aurait un mouvement circulaire et régulier, on aurait et seul le deuxième terme, R, appelé réduction à l'équateur et dû à l'obliquité , interviendrait. Remarquer que si on avait (le soleil en permanence dans le plan de l'équateur), ce dernier terme serait nul.

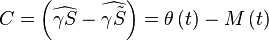
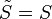
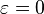
• À l'aide d'un développement limité, et en posant , le terme de la réduction à l'équateur ci-dessus peut s'écrire