Géométrie symplectique - Définition
La liste des auteurs de cet article est disponible ici.
Présentation générale
Géométrie symplectique linéaire
La géométrie euclidienne concerne les espaces affines euclidiens E : à ces derniers sont associées une distance naturelle, appelée distance euclidienne, unique invariant pour l'action diagonale du groupe des isométries affines de E sur E2, et une notion d'angle. Les distances et angles définis par un ensemble de points de E sont préservés sous l'action d'une isométrie.
En oubliant la notion de distance, il est loisible de s'intéresser uniquement au volume euclidien. Il est bien connu qu'un isomorphisme linéaire affine préservant le volume est de déterminant +1 ou -1. Malheureusment, en dimension n, on perd ainsi toute information sur les configurations d'au plus n-1 points.
La géométrie symplectique linéaire apparaît comme une géométrie intermédiaire, dans laquelle on perd la notion de distance, tout en conservant une notion d'aire orientée, et donc un invariant associé à 3 points. À trois points A, B et C d'un espace vectoriel réel E doit être associée une aire a(ABC). Pour des raisons d'additivité et de monotonicité des aires, cette quantité doit s'écrire :
- a(ABC) = ω(AB,AC),
où
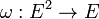
- ω(u,v) = − ω(v,u).
Cette forme est dite non-dégénérée lorsque, pour tout vecteur
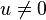
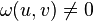
Un isomorphisme linéaire ou affine de E est dit symplectique lorsqu'il préserve la forme symplectique ω. L'ensemble des isomorphismes linéaires symplectiques de Cn forme un groupe, appelé le groupe symplectique, noté Sp(n) ou Sp(2n) suivant les auteurs. C'est un groupe de Lie classique connexe non compact de dimension n(n-1)/2. Il contient le groupe unitaire U(n) comme rétracte par déformation forte : ces deux groupes ont donc le même type d'homotopie.
La classification des ellipsoïdes dans un espace euclidien de dimension 2n modulo les isométries est donnée par 2n invariants, qui sont leurs diamètres respectifs. Par opposition, comme observé par Hofer et Zehnder, la classification des ellipsoïdes d'un espace symplectique modulo les applications affines symplectiques est donné par n invariants.
Géométrie symplectique
Les variétés différentielles s'obtiennent par des recollements d'ouverts d'espaces vectoriels réels de dimension finie suivant des difféomorphismes. Un intérêt porté sur des structures particulières peut conduire à imposer des restrictions sur la nature de ces recollements.
L'objet d'étude de la géométrie symplectique est les 2-formes différentielles fermées non dégénérées. Une telle forme différentielle est appelée forme symplectique. Sur une variété différentielle M, on se donne une forme antilinéaire non dégénérée ωx, et on demande à ce que la collection
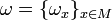
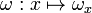
-
![X\cdot\omega(Y,Z)+Y\cdot \omega(Z,X)+Z\cdot \omega(X,Y)=\omega([X,Y],Z)+\omega([Y,Z],X)+\omega([Z,X],Y)](https://static.techno-science.net/illustration/Definitions/autres/c/cafb42aa9353df8939a401fa92557f92_97cc849edca7a6fdb08196089fd46447.png)
Une variété munie d'une forme symplectique est appelée variété symplectique. Une fois les objets d'étude définis, on a coutume de s'intéresser aux relations qu'ils peuvent entretenir entre eux. Un difféomorphisme
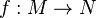
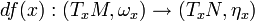
L'ensemble des difféomorphismes symplectiques de (M,ω) forment un groupe, appelé groupe des difféomorphismes symplectiques, et noté Symp(M,ω). Son étude a un intérêt de premier plan.
L'un des principaux résultats élémentaires de la géométrie symplectique est le théorème de Darboux : localement, deux variétés symplectiques de même dimension sont isomorphes. Dit autrement, aucun invariant local n'existe. Sur ce point, et pas le moindre, la géométrie symplectique s'oppose complètement à la géométrie riemannienne :
- En géométrie riemannienne, l'existence d'invariants de classe C2 se traduit par un groupe d'isométries de dimension finie et une quantité infinie de classes d'équivalence de métriques riemanniennes.
- En géométrie symplectique, l'inexistence d'invariants locaux au contraire donne un groupe de dimension infinie de difféomorphismes symplectiques et un ensemble "discret" de classes d'équivalence de formes symplectiques.
Cette dichotomie résume bien l'opposition entre la souplesse de la géométrie riemannienne contre la rigidité de la géométrie symplectique. Cette rigidité se retrouve à bien d'autres niveaux (rigidité des symplectomorphismes, théorème de rigidité de Gromov, ...).
Variétés symplectiques
Les espaces de phases étudiés jusqu'à maintenant étaient assez simples car nous étions partis d'espaces de configurations assez simples. Cependant, dans l'exemple du pendule simple, il eut été plus logique de considérer que la variable q1 vivait dans une cercle et pas dans une droite. Plus généralement, on peut imaginer des espaces de configuration arbitrairement compliqués, par exemple si un point est astreint à se déplacer sur une surface ayant une forme sophistiquée.
Quelle que soit la complexité de l'espace de configuration on peut toujours lui associer un espace des phases appelé fibré cotangent de l'espace de configuration et qui est toujours muni d'une structure symplectique canonique. Les théorèmes de Liouville, Poincaré, Noether et Liouville-Arnold restent vrais et on peut donner des analogues du théorème de Gromov dans ce cadre plus général.
Définition et théorème de Darboux
On peut vouloir aller plus loin dans la généralisation et étudier tous les espaces munis d'une structure symplectique. Pour cela il faut revenir un peu plus en détail sur la définition d'une structure symplectique. À partir de maintenant on considère un variété M de dimension 2n, c'est-à-dire un ensemble qui peut localement être paramétré par 2n nombres. Comme expliqué plus haut, une structure symplectique sur M est une application qui, à toute surface dans M, associe un nombre et qui vérifie en plus deux propriétés. La première est que cette structure doit permettre d'associer un volume à toute partie de dimension 2n de M en procédant comme expliqué dans le paragraphe sur le théorème de Poincaré. La deuxième condition est que le nombre associé à toute surface sans bord est nul.
Le passage des espaces de phases aux variétés symplectiques générales est une grande généralisation mais on peut montrer qu'une variété symplectique ressemble toujours localement à un espace de phases. C'est le théorème de Darboux : au voisinage de n'importe quel point, toute variété symplectique peut être paramétré par un espace de phase de sorte que toute surface assez petite se voit attribuer le même nombre par la structure symplectique donnée et par la structure symplectique de l'espace des phases.
Existence et classification
La question de savoir quels ensembles admettent au moins une structure symplectique est difficile. On connaît de nombreux exemples, des conditions nécessaires, d'autres qui sont suffisantes mais aucune caractérisation complète.
De même, une fois l'existence acquise on ne sait que très rarement combien de structures symplectiques réellement différentes cohabitent sur un même ensemble.
Symplectomorphismes
L'étude de la géométrie symplectique est née du constat que l'évolution d'un système mécanique préserve la structure symplectique canonique de l'espace des phases. Plus généralement on peut chercher à comprendre l'ensemble des transformations qui préservent une structure symplectique donnée. De telles transformations sont appelées symplectomorphismes et sont toujours très nombreuses, elles forment un ensemble de dimension infinie appelé groupe des symplectomorphismes. Pour comprendre la forme de cet ensemble, on cherche à le comparer à des ensembles plus petits que l'on comprend mieux. Les premiers résultats significatifs dans ce domaine sont dus à Gromov dans la foulée de son théorème de non-tassement.
Interactions
- Géométrie complexe : De nombreux exemples de structures symplectiques et de nombreuses questions viennent de la géométrie complexe. Ainsi pour (presque) toute équation polynomiale en plusieurs variables complexes, l'ensemble des solutions est muni d'une structure symplectique. L'étude de ces équations et des structures symplectiques s'éclairent l'une l'autre et c'est en transposant au cas symplectique général des idées nées dans le contexte de la géométrie complexe que Gromov a obtenu son théorème de non-tassement et de nombreux autres résultats révolutionnaires.
- Géométrie de contact : La géométrie de contact est une autre branche de recherche en géométrie qui entretient des liens tellement étroits que certains auteurs présentent la géométrie de contact comme un analogue en dimension impaire de la géométrie symplectique. Sous des circonstances favorables, le bord éventuel d'une variété symplectique hérite d'une structure de contact (la variété symplectique est alors appelée remplissage de la variété de contact) ; de nombreux problèmes se posent, comme l'existence d'un tel remplissage ou l'existence de caractéristiques fermées (lire à ce sujet Conjecture de Weinstein).
- Systèmes dynamiques (différentiables) : Les développements en géométrie symplectique ont été motivées par les conjectures d'Arnold concernant l'estimation du nombre de points fixes minimal d'un symplectomorphisme sur une variété symplectique compacte (voir Histoire). En retour, l'intégration de champs de vecteurs spécifiques dépendant du temps sur des variétés symplectiques donnent lieu à une classe particulière de symplectomorphismes, appelés difféomorphismes hamiltoniens. Les termes dynamique hamiltonienne ou système hamiltonien sont d'usage courant.
- Ergodicité : La n-ième puissance d'une forme symplectique sur une variété de dimension 2n est une forme volume, préservée par les symplectomorphismes. Des travaux de Polterovich portent sur les propriétés ergodiques de ces difféomorphismes, et en particulier donnent des estimations de leurs entropies métriques.
- Géométrie riemannienne : Une famille importante de variétés symplectiques est donnée par les variétés cotangentes.
- Géométrie algébrique : Suite aux travaux de Gromov, un certain nombre de concepts de géométrie complexe s'adaptent en géométrie symplectique : courbes holomorphes, invariants de Gromov-Witten, ...

















































