Mathématiques - Définition

Mathématiques et philosophie

Les questions traditionnelles que se pose la philosophie au sujet des mathématiques peuvent se classer selon trois thèmes :

1. La nature des objets mathématiques : s'ils existent par eux-mêmes, ou bien s'ils sont des constructions mentales ? Quelle est la nature d'une démonstration ? Quelles sont les liens entre la logique et les mathématiques ?
2. L'origine de la connaissance mathématique : d'où vient la vérité des mathématiques, et de quelle nature est-elle ? Quelles sont les conditions pour que des mathématiques existent, et leur lien avec l'homme ? Quels sont les impacts de la structure de la pensée humaine sur la forme et le développement des mathématiques actuelles ? Les limites qu'elle induit?
3. La relation des mathématiques avec la réalité : quelle relation les mathématiques abstraites entretiennent-elles avec le monde réel ? Quels sont les liens avec les autres sciences ?

Les mathématiques sont parfois surnommées « reine des sciences ». Cependant, l'expression remonte à Carl Friedrich Gauss : Regina Scientiarum et le mot scientiarium signifie en réalité « des connaissances ».

Impact culturel

Expression artistique

Les notes qui sonnent bien ensemble à une oreille occidentale sont des sons dont les fréquences fondamentales de vibration sont dans des rapports simples. Par exemple, l'octave est un doublement de fréquence, la quinte une multiplication par 3/2.

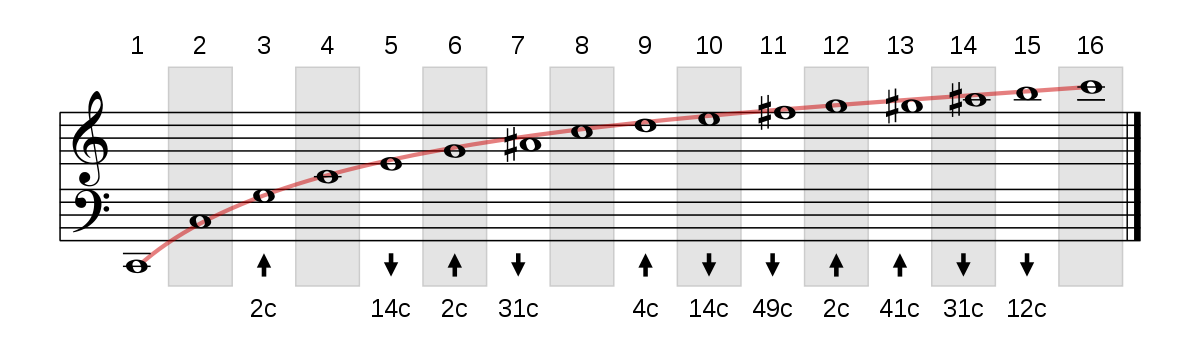
Ce lien entre les fréquences et l'harmonie a été notamment détaillé dans le Traité de l'harmonie réduite à ses principes naturels de Jean-Philippe Rameau, compositeur baroque français et théoricien de la musique. Il repose en partie sur l'analyse des harmoniques (notées 2 à 15 dans la figure suivante) d'un son fondamental Do grave (noté 1), les premières harmoniques et leurs octaves sonnant bien entre elles.

Si la courbe tracée en rouge, qui suit les notes harmoniques, a une allure logarithmique, cela correspond au rapport entre deux phénomènes:

• d'une part, la représentation de la hauteur d'un son par notre système auditif qui est proportionnelle au logarithme de la fréquence du son (une fréquence double correspond toujours à la même « distance sonore » appelée octave).
• d'autre part, les fréquences harmoniques qui sont des multiples entiers de la fréquence fondamentale.

Les Occidentaux associent une certaine beauté aux figures symétriques. Une symétrie d'une figure géométrique est, intuitivement, l'existence d'un motif de la figure qui se répète suivant une règle précise, tout en étant partiellement transformé. Mathématiquement, une symétrie est l'existence d'une action non triviale d'un groupe, très souvent par isométrie, c'est-à-dire qui préserve les distances sur la figure. En d'autres termes, l'intuition de la règle est mathématiquement réalisée par le fait que c'est un groupe qui agit sur la figure, et le sentiment qu'une règle régit la symétrie est précisément dû à la structure algébrique de ce groupe.

Par exemple, le groupe lié à la symétrie miroir est l'ensemble . Un test de Rorschach est une figure invariante par cette symétrie, de même qu'un papillon et plus généralement le corps des animaux, du moins en surface. Lorsqu'on dessine la surface de la mer, l'ensemble des vagues possède une symétrie par translation : bouger notre regard de la longueur séparant deux crêtes de vagues ne change pas la vue que l'on a de la mer. Un autre cas de symétrie, cette fois non isométrique et presque toujours seulement approximative, est celui présenté par les fractales : un certain motif se répète à toutes les échelles de vision.

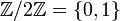
Vulgarisation

La vulgarisation mathématique a pour objectif de présenter les mathématiques en un langage dénué de termes techniques. Comme l'objet d'études des mathématiques n'est pas réel, elle use souvent d'un vocabulaire imagé, et de comparaisons ou analogies non rigoureuses, pour faire sentir l'idée des développements mathématiques. Parmi les ouvrages qui se fixent ce but, citons Oh, les maths de Yakov Perelman et Le livre qui rend fou de Raymond Smullyan. Toutefois, les mathématiques font rarement l'objet de vulgarisation dans des journaux écrits ou télévisés.

La revue Tangente, l'aventure mathématique, est le principal magazine de vulgarisation mathématique édité en France.

La revue Images des mathématiques, soutenue par le Centre national de la recherche scientifique (CNRS), relève également le défi. Elle fait découvrir au plus grand nombre la recherche mathématique contemporaine et son environnement.

Littérature et filmographie

Si nombre de biographies portent sur les mathématiciens, les mathématiques sont un thème certes peu exploité dans la littérature ou la filmographie, mais présent.

Romans

• Plusieurs livres de Denis Guedj, dont :
  • Le Théorème du Perroquet
  • Zéro, ou les cinq vies d'Aémer
• Le Démon des maths de Hans Magnus Enzensberger
• Mathématique du crime de Guillermo Martinez
• Flatland, d'Edwin Abbott Abbott

Films

• Will Hunting
• Un homme d'exception, film de Ron Howard (2001)
• Pi, film de Darren Aronofsky (1998)
• La preuve irréfutable, (2005) [1]
• Cube, Cube 2 et Cube Zero
• Crimes à Oxford.
• C'est la tangente que je préfère [2] .

Théâtre

Pièces de théâtre

• La Preuve de David Auburn, 2000 (Proof, Ed. Dramatist's Play Service, 2002)

Spécialistes de théâtre de sciences

• Le Théâtre scientifique de Louis Figuier, Fabienne Cardot, Revue Romantisme, 1989
• Théâtre et sciences, Le double fondateur, Jacques Baillon, L'Harmattan, 1998
• La Recherche théâtrale dans un institut technologique et scientifique, Ouriel Zohar, dans Théâtre et Science, Ed. Prof. Lucile Garbagnati, F. Montaclair and D. Vingler, Presses du Centre Unesco de Besançon et du Théâtre de l' Université de Franche-Comté, Besançon, 1998.
• Théâtre et matière, Les moteurs de représentation, Jacques Baillon, L'Harmattan, 2002
• Le Théâtre de sciences, Michel Valmer, CNRS Éditions, 2006
• Science on stage, from Dr Faustus to Copenhagen, Kirsten Sheperd-Barr, Princeton University Press, 2006.
• Le Modèle scientifique dans le théâtre de Tom Stoppard, Liliane Campos, dans Epistémocritique, Revue d'études et de recherches sur la littérature et les savoirs, vol. II, 2008
• L'île logique, théâtre et clowns sur la logique, les mathématiques et la physique théorique (CNRS, école Polytechnique), Cédric Aubouy. 2008.

Séries télévisées

• Numb3rs, série de Nicolas Falacci et Cheryl Heuton.
• Eureka, série télévisée créée par Andrew Cosby et Jaime Paglia.