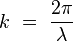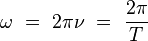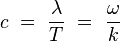Onde - Définition

Dimensionnalité

Soient le déplacement de l'energie et la vitesse de l'onde :

•  : l'onde est longitudinale.

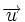
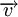
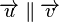
exemple : Ressort à boudin. Si on déplace brutalement une spire d'un tel ressort tendu entre deux supports on voit se former une onde de compression des spires. Dans ce cas le mouvement des spires se fait dans la même direction que la propagation de l'énergie, suivant la droite que constitue l'axe de symétrie du ressort. Il s'agit d'une onde longitudinale à une dimension.

•  : l'onde est transversale.

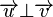
Exemples : Lorsqu'on frappe un tambour, on crée sur sa peau une onde transverse à deux dimensions, comme dans le cas de la surface de l'eau.

Lorsqu'on déplace des charges électriques, les champs magnétiques et électriques locaux varient pour s'adapter à la variation de position des charges produisant une onde électromagnétique. Cette onde est transverse et peut se propager dans les trois directions de l'espace. Dans ce cas, l'onde n'est pas un déplacement de matière.

• Une onde peut être à la fois longitudinale et transversale.

Exemple : Sur la mer, une vague est créée par un vent qui provoque une variation de la hauteur d'eau. Il en est de même pour les ronds dans l'eau provoqués par la chute d'un caillou. Dans ce cas on peut facilement voir que la propagation de l'onde se fait dans les deux dimensions de la surface de l'eau.

Ondes et stabilité d'un milieu

Pour que des ondes se propagent dans un milieu il faut que celui-ci soit stable: sous l'action d'une perturbation extérieure, le milieu doit développer un mécanisme de rappel le ramenant vers sa position d'équilibre. La nature et les propriétés de l'onde dépendent de la manière dont ce mécanisme agit. Ainsi, par exemple, pour les vagues, ce mécanisme de rappel est la pesanteur tendant à ramener la surface libre vers une position d'équilibre. Pour les ondes sonores, le mécanisme de rappel est la tendance d'un fluide à uniformiser sa pression. Pour les ondes de torsion (comme sur un violon joué à l'archet), le mécanisme de rappel est le couple exercé par la corde.

Modélisation d'une onde progressive

Une onde se modélise par une fonction A(x,t), d'amplitude A, x étant la position dans l'espace (vecteur) et t étant le temps.

Une très grande famille des solutions d'équations de propagation des ondes est celle des fonctions sinusoïdales, sinus et cosinus (elles ne sont pas les seules). On montre également que tout phénomène périodique continu peut se décomposer en fonctions sinusoïdales (série de Fourier), et de manière générale toute fonction continue (transformée de Fourier). Les ondes sinusoïdales sont donc un objet d'étude simple et utile.

Dans ce cadre, une onde sinusoïdale peut s'écrire :

(Démonstration)

On appelle

• amplitude le facteur A₀,
• phase l'argument du sinus ,
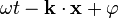
• tandis que φ est la phase à l'origine lorsque t et x sont nuls.

La phase absolue d'une onde n'est pas mesurable. La lettre grecque ω désigne la pulsation de l'onde on note qu'elle est donnée par la dérivée de la phase par rapport au temps :

.

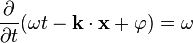
Le vecteur k est le vecteur d'onde. Lorsque l'on se place sur un seul axe, ce vecteur est un scalaire et est appelé nombre d'onde : c'est le nombre d'oscillations que l'on dénombre sur 2π unités de longueur.

On a pour la norme du vecteur d'onde :

La pulsation s'écrit en fonction de la fréquence ν :

La vitesse de phase vaut enfin :

Périodicité temporelle et périodicité spatiale

Phénomène ondulatoire

Le cas le plus simple d'onde progressive périodique est une onde dite « monochromatique ».

Onde progressive vue à plusieurs instants successifs

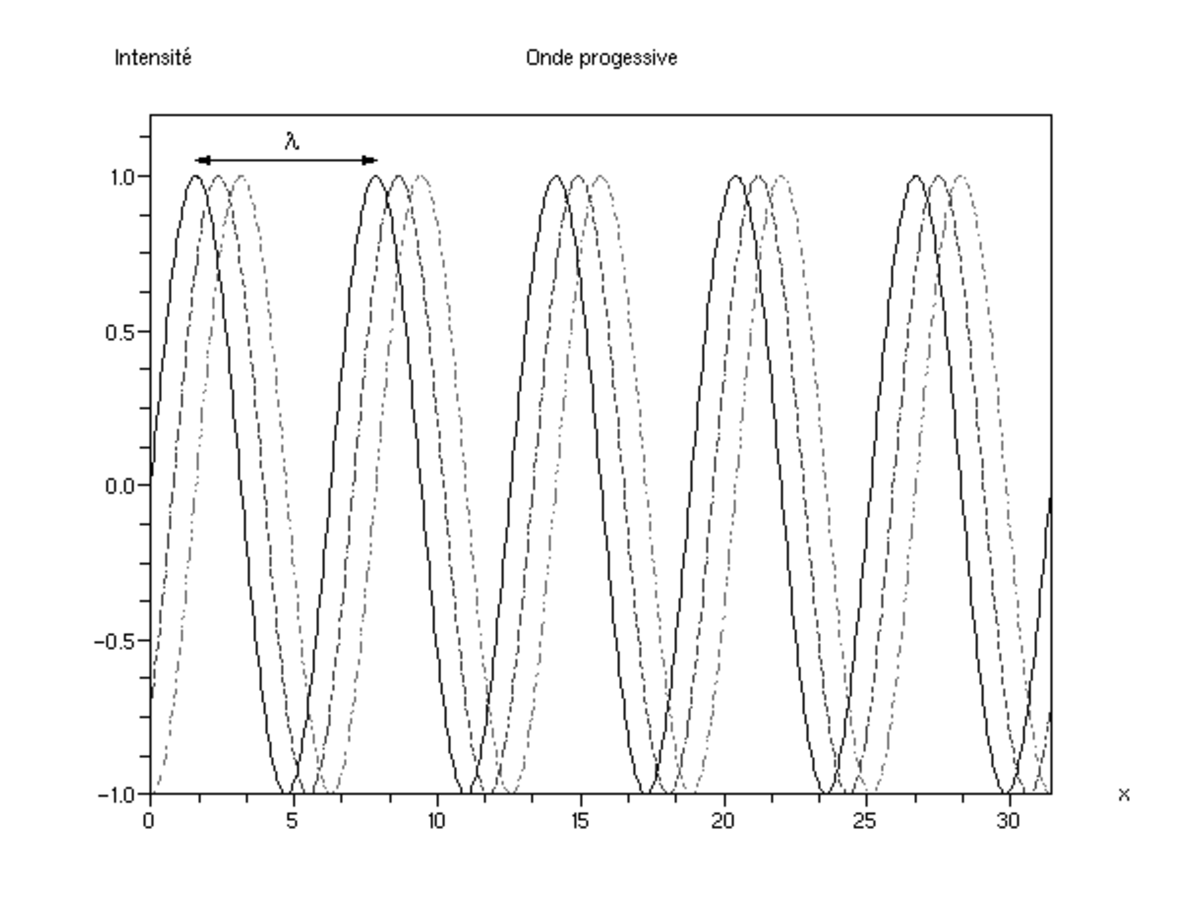
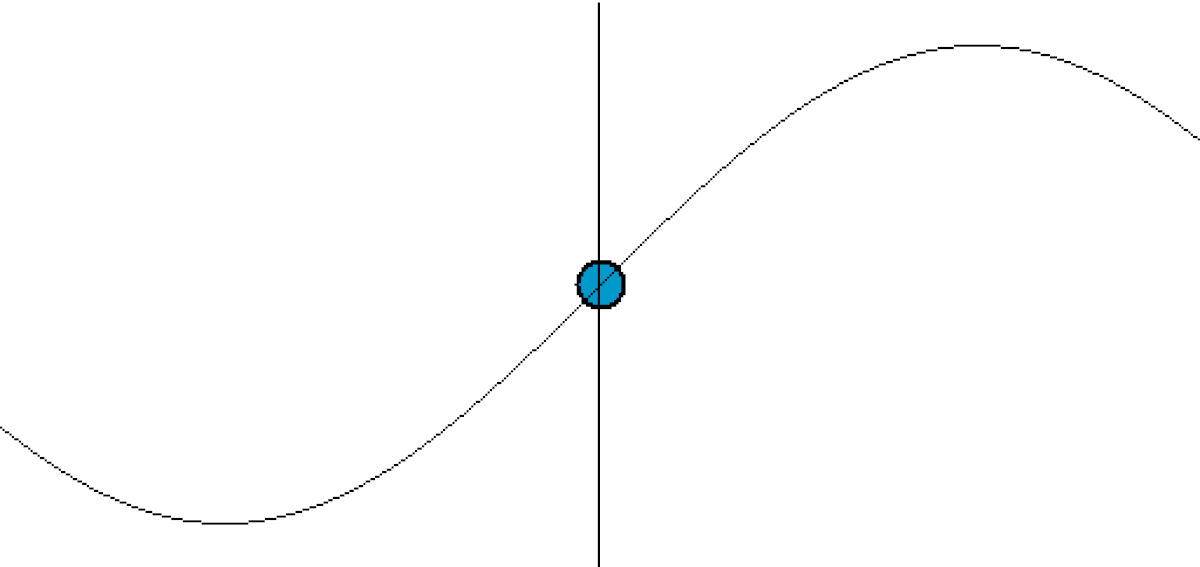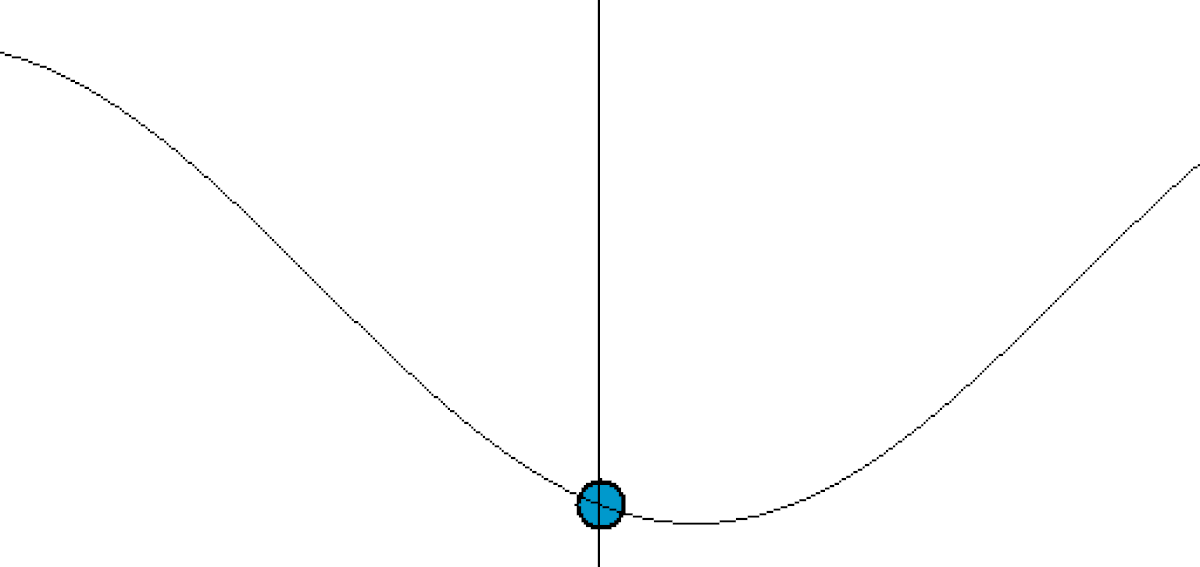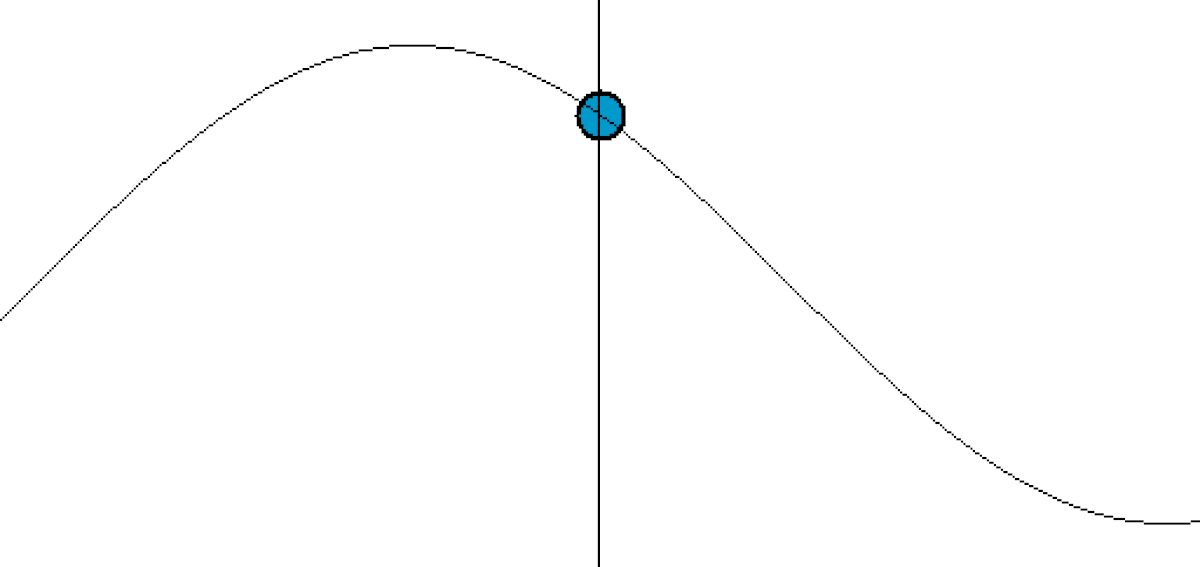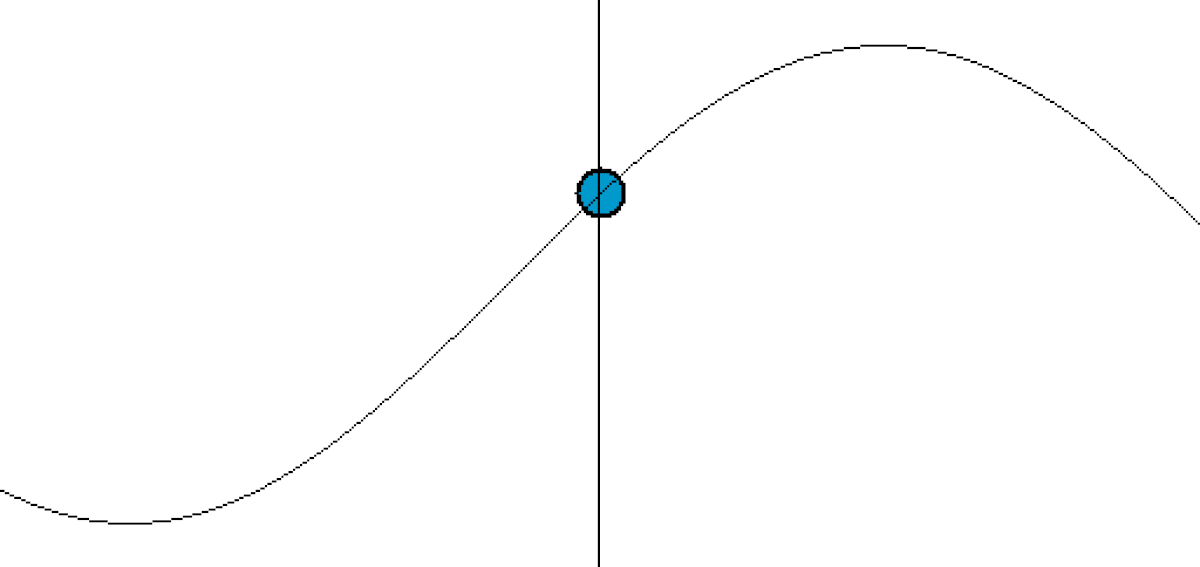
Si l'on prend un cliché du milieu à un moment donné, on voit que les propriétés du milieu varient de manière sinusoïdale en fonction de la position. On a donc une périodicité spatiale ; la distance entre deux maxima est appelée longueur d'onde, et est notée λ. Si l'on prend des photographies successives, on voit que ce « profil » se déplace à une vitesse nommée vitesse de phase.

Effet d'une onde en un endroit donné : variation cyclique de l'intensité

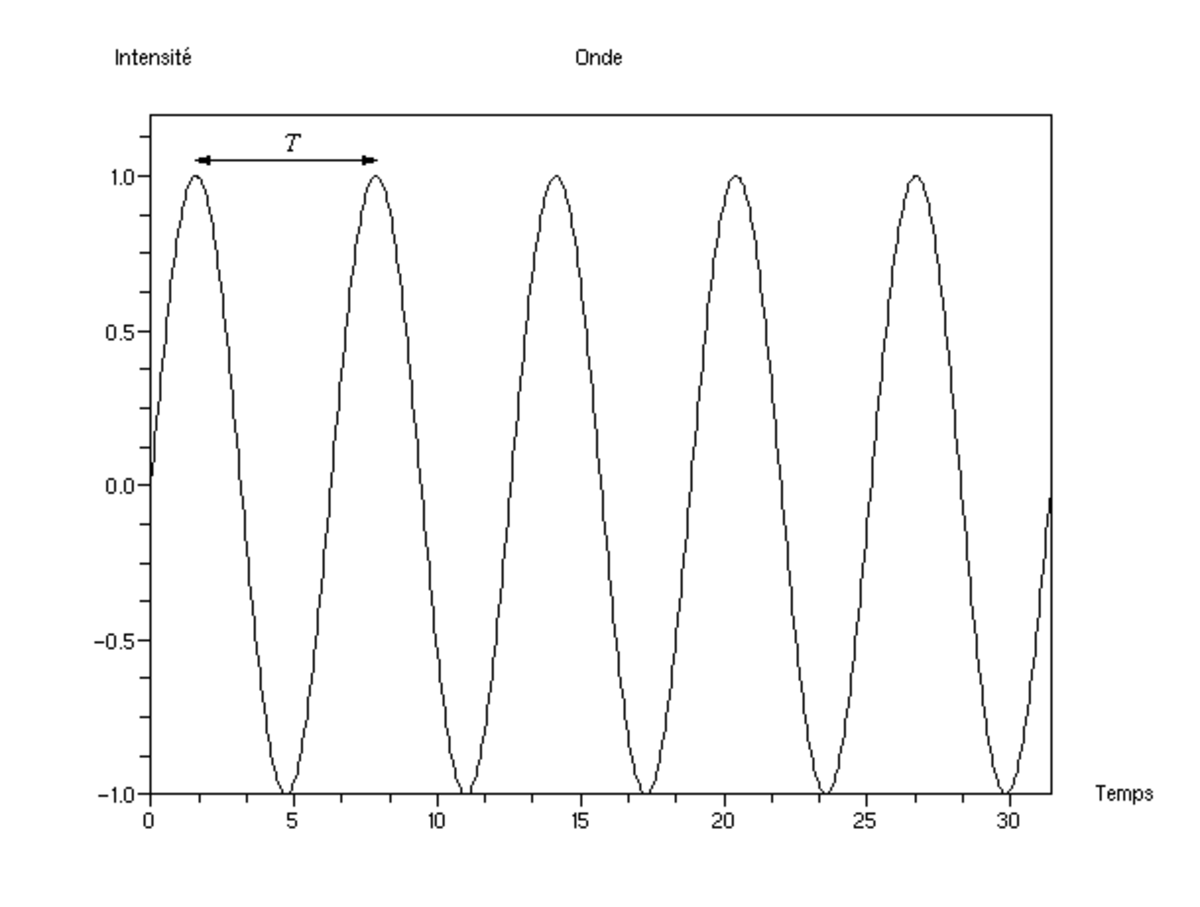
Si l'on se place à un endroit donné et que l'on relève l'intensité du phénomène en fonction du temps, on voit que cette intensité varie selon une loi, elle aussi sinusoïdale. Le temps qui s'écoule entre deux maxima est appelé période et est noté T.