Optique métaxiale - Définition

Introduction

L'optique métaxiale constitue une synthèse entre l'optique géométrique et l'optique physique. Elle a pour spécificité de rendre compte simultanément du phénomène d’imagerie du couple Champ-Cohérence, ainsi que de ses transformations fonctionnelles, qui sont les constituantes d’une optique ondulatoire de Fourier. De façon à pouvoir mieux situer cette doctrine métaxiale, il est bon d’établir une comparaison thème par thème avec l’optique géométrique.

Optique Géométrique

L’Optique géométrique se préoccupe uniquement du transfert par imagerie de l’Intensité lumineuse ; association réalisée entre un objet émetteur et un écran récepteur particulier, séparés par un ensemble de milieux homogènes et de dioptres, qui sont les constituants du Système optique utilisé.

Outil

L’outil de ce transfert repose sur le postulat des Rayons lumineux, soumis au Principe de Retour inverse et réfractés suivant la Loi de Snell.

Approximation géométrique

Cette Optique géométrique postule, pour les systèmes en cause, des dimensions transversales extrêmement faibles à l’échelle des dimensions longitudinales ; d’où son nom d’Optique paraxiale. De ce fait, toutes les surfaces (objet, émetteur, dioptres) peuvent se représenter dans une approximation du premier ordre, donc par leurs seuls plans tangents au sommet.

Transfert

Le système paraxial délivre, sur l’écran-image, une copie de la répartition de l’Intensité lumineuse rayonnée par la surface-objet. Le pôle de l’écran-image est le conjugué géométrique de celui du plan de l’objet, selon une relation donnée par la Formule de Descartes, conséquence de la Loi de Snell. L’imagerie en intensité s’effectue point par point, à l’échelle du grandissement , quantité qui dépend de la position de l’objet.

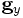
Système équivalent

Un système optique peut se réduire à un système équivalent formé de deux foyers et de deux plans principaux. Ces derniers ont pour pôles respectifs les deux points conjugués géométriques par le système initial pour le grandissement .

Optique Métaxiale

L’Optique Métaxiale a pour mission de rendre compte du transfert du couple Champ électromagnétique-Cohérence entre une surface émettrice et une surface réceptrice arbitrairement choisie, séparés par un ou plusieurs milieux homogènes.

Outil

L’outil de ce transfert concerne les opérateurs spatiotemporels agissant sur un Champ électromagnétique, aléatoire et polychromatique, ainsi que, simultanément, sur sa Cohérence. Il écarte tout postulat, en s’appuyant sur les seules Equations de Maxwell de l’électromagnétisme et sur le Principe de Réciprocité : il s’intègre donc entièrement dans une optique physique, pour laquelle il s’attache à appliquer les concepts et méthodes de la Théorie des Signaux et des Systèmes.

Dans cette théorie, le transfert d’un Système est parfaitement défini dès lors que l’on connaît le Gain Complexe (alias Fonction de transfert) de ce dernier. Un tel concept correspond, dans notre cas, à l’Amplitude complexe du Champ perçu sur l’Ecran, à travers le Système optique, à partir du rayonnement d’une source ponctuelle, unitaire et monochromatique située sur l’Objet.

Toute l’étude repose alors sur la détermination de l’expression analytique d’un tel Gain Complexe, tant pour le Champ que pour sa Cohérence. Or, la théorie du filtrage des signaux aléatoires (cf. Formule des Interférences ) fait apparaître une propriété fondamentale : la Cohérence d’un couple de points est transférée, à travers un Système, par un « Opérateur de Cohérence », associé univoquement aux « Opérateurs de Champ » relatifs aux points en cause. Cela fait que la connaissance des règles et des propriétés du transfert du Champ entraîne ipso-facto celle des règles et des propriétés du transfert de la Cohérence ; grâce à quoi, on peut faire l’économie d’une étude séparée, qui aurait été consacrée à la seule Cohérence.

Approximation géométrique

L’Optique métaxiale postule également, pour les systèmes en cause, des dimensions transversales faibles à l’échelle des dimensions longitudinales, mais avec une exigence moindre que pour le domaine paraxial. Ainsi, par hypothèse, toutes les surfaces (objet, émetteur, dioptres) peuvent se représenter, dans le modèle métaxial, avec une approximation du second ordre , donc par leurs seules sphères osculatrices au sommet. Relativement au modèle paraxial, on gagne ainsi plusieurs ordres de grandeur sur les dimensions transversales prises en compte.

L’approximation métaxiale fait que les angles d’inclinaison sur l’axe sont peu élevés. Elle permet ainsi de se limiter à une description scalaire du Champ électromagnétique et de faire alors intervenir la simple Equation de Kirchhoff. Par suite, cette doctrine métaxiale, qui englobe déjà toute la Radioélectricité, depuis le spectre des LF jusqu’aux rayons X, en passant par les UHF (Radar), peut s’appliquer sans modification à l’Acoustique des Fluides (Sonar).

C’est pourquoi nous utilisons de préférence le terme plus général de Diffraction Métaxiale.

Transfert

Trilogie

Dans le cas le plus simple d’un milieu homogène unique , le modèle métaxial décrit le transfert entre un objet rayonnant et un écran du même milieu par une transformation fonctionnelle du Champ (ou de sa Cohérence) laquelle va s’intègrer dans une « Trilogie » , formée de la combinaison (opérée dans l’ordre) :

• d’une Transformée de Fourier (TF) spatiale ,
• d’un Filtrage de Fresnel ,
• d’une Transparence de courbure .

Les détails de cette Trilogie sont donnés plus loin ( § 2.35 à 2.37).

Imagerie cohérente.

Dans le cas général d’un champ rayonnant présent sur un objet de l’espace amont d’un Système formé de plusieurs milieux séparés par des dioptres, le modèle métaxial implante, dans le milieu aval du système, une réplique cohérente de cet objet (Champ et Cohérence) répartie sur une surface bien déterminée, la « Sphère-image » .

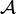
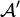
Cette réplique se comporte à son tour comme un objet secondaire appartenant à l’espace aval ; intermédiaire immatériel susceptible de rayonner vers n’importe quel écran de cet espace et qui, quantitativement, se substitue entièrement à l’ensemble « Objet + Système » .

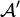
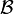
La Sphère-image

La Sphère-image est décrite par :

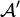
- un pôle , qui est le conjugué géométrique, au sens de la Formule de Descartes, du pôle de la sphère-objet , - un centre de courbure, également conjugué géométrique du centre de l’objet.

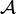
L’ Imagerie cohérente qu’elle délivre est caractérisée par :

• un facteur d’échelle de la réplique, donné par le grandissement gy à l’endroit du pôle de la sphère-image.
• un facteur d’amplitude du champ qui vaut  ; celui de la cohérence valant

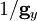
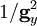
Tétralogie

Le transfert entre la sphère-image , en tant qu’objet secondaire, et la sphère choisie comme écran véritable constitue bien un transfert dans un milieu homogène unique , ici le milieu aval. Décrit dans le modèle métaxial , ce type de transfert entre donc dans le cadre de la « Trilogie » déjà évoquée.

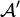
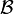
L’ensemble «  Imagerie cohérente + Trilogie  » correspond au comportement le plus général du transfert, à travers un système, entre un objet amont connu et un écran matériel aval déterminé arbitrairement : il portera le nom de « Tétralogie ».

Transformée de Fourier spatiale

Elle traduit une diffraction de Fraunhofer intermédiaire. Celle-ci est uniquement liée à la structure de l’objet : position et courbure .

La TF spatiale est perçue (Champ et Cohérence) sur la «  Sphère de Fourier » associée à l’objet (réel ou secondaire) par une permutation pôle-centre :

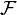
• son pôle est le centre de courbure de l’objet,
• son centre de courbure est le pôle de l’objet.

Dans le cas particulier où la répartition sur la sphère-objet se limite à un champ monochromatique (longueur d’onde λ) et monofréquentiel (fréquence spatiale ) le champ induit sur la sphère de Fourier se réduit à un point unique. Le vecteur qui décrit la direction de ce point, une fois normalisé et projeté sur un plan orthogonal à l’axe, fournit la fréquence angulaire . On aboutit alors à la très importante « Loi d’Ohm métaxiale », , laquelle relie la fréquence spatiale, caractéristique de la structure d’un objet et la fréquence angulaire, caractéristique de sa diffraction.

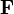
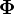
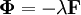
Filtrage de Fresnel

Ce filtrage est associé à la seule position de l’écran matériel .

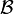
On prend pour seconde surface intermédiaire une sphère concentrique avec la sphère de Fourier  : la Sphère Cardinale , qui est telle que :

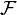
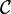
• son pôle est celui de la surface choisie comme écran véritable,
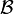
• son centre de courbure est le pôle de l’objet.

Le passage de la Sphère de Fourier à la Sphère Cardinale concentrique se traduit par un produit de convolution spatial : constituant déjà un filtrage temporel, il réalise ainsi un filtrage spatiotemporel, le Filtrage de Fresnel, deuxième composante de la Trilogie.

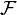
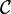
Dans ces conditions, le transfert direct de l’objet rayonnant vers la Sphère Cardinale , apparaît analytiquement comme le résultat d’une Transformée de Fourier-Fresnel (géneralisée). Un tel comportement est valable pour le Champ analytique aussi bien que pour la Cohérence.

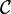
Transparence de Courbure

La dernière opération de la Trilogie ne dépend que de la courbure de l’écran final .

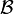
Elle concerne en effet le passage de la Sphère Cardinale vers cet écran . Les deux sphères possédant déjà un même pôle, il suffit de passer de la courbure de à celle de . Une telle opération se traduit par l’intervention d’un facteur complexe, de module unité, agissant sur le Champ analytique (il en est de même pour la Cohérence). Un tel comportement est celui d’une transparence : la Transparence de courbure.