Théorie des équations (histoire des sciences) - Définition

Nouveau départ

Viète, Fermat et Descartes

En découvrant le calcul littéral, François Viète trouve un langage formel donnant à l’algèbre son autonomie par rapport à la géométrie.

Le début d'une véritable théorie des équations est généralement attribué à Viète, mathématicien français de la fin du XVI^e siècle. S’il refuse encore de considérer les avancées de Bombelli, c’est-à-dire les nombres négatifs ou imaginaires, il réalise néanmoins trois avancées majeures.

La plus célèbre est probablement celle qu’il appelle la logique spécieuse et que l’on qualifie maintenant de calcul littéral. Viète réunit deux usages des lettres en mathématiques. Celui de l'algèbre se répand et se perfectionne en Europe au cours du XVI^e siècle, mais apparaissait déjà chez Diophante : une lettre s’additionne ou se multiplie et joue le rôle d’inconnue dans une équation. Celui de la géométrie est courant dès l'Antiquité : une lettre désigne une grandeur ou un objet non spécifié, point, droite, distance entre deux points sur une figure … Les principes généraux de résolution des équations ne peuvent être établis qu'à l’aide de la géométrie, comme l’usage de gnomons pour les identités remarquables, puis illustrés par des exemples d’équations polynomiales aux coefficients numériques, que Viète considère comme appartenant à la logique numéreuse. Viète introduit une deuxième catégorie de lettres pour les coefficients. Ceux-ci sont aussi des valeurs considérées comme fixées, même si on ne les connaît pas : c'est ce qu'on appelle maintenant un paramètre. En transportant une ancienne habitude géométrique à l’algèbre, Viète crée la logique spécieuse. Cette nouvelle approche revient à considérer une équation comme une expression du type : aX² + bX = c. Réussir à résoudre cette équation c’est être capable de résoudre toutes les équations du second degré, un unique cas général de logique spécieuse permet de traiter une infinité de cas particuliers issus de la logique numéreuse.

À ce premier apport, Viète ajoute le développement d’un langage symbolique permettant d’exprimer plus simplement une expression polynomiale. Les idées de Viète permettent une expression plus limpide que celle de ses prédécesseurs. Son vocabulaire est toujours en partie d’actualité : on lui doit le terme de coefficient ainsi que celui de polynôme.

Ce formalisme permet d’exprimer les premiers résultats généraux, au sens ou ils sont indépendants du degré du polynôme, comme la relation entre les coefficients et les racines d’un polynôme.

Le système de notations de Viète est repris par Fermat et Descartes pour, d’après Nicolas Bourbaki, devenir « à peu de choses près, celui que nous utilisons aujourd’hui. » Ces travaux permettent un renversement de la hiérarchie mathématique. Jusqu’à Viète, la théorie des équations est nécessairement une émanation de la géométrie. L’unique méthode générique de démonstration se fonde sur les Éléments d’Euclide et les calculs-clés, comme les identités remarquables, sont établis à l’aide de considérations géométriques. Le calcul littéral permet d’affranchir l’algèbre de ces contraintes. Pour Descartes, l’algèbre, additionnée de l’usage d’un repère cartésien, devient une machine à démontrer des théorèmes géométriques. Elle est une « extension de la logique, dénuée de toute signification par elle-même, mais indispensable pour le maniement des quantités, et, en un sens, plus fondamentale même que la géométrie. »

Calcul infinitésimal

La deuxième moitié du XVII^e siècle est l’époque d’un séisme appelé calcul infinitésimal. L’étude des trajectoires et des mouvements, issue de la physique, est à l’origine de nouvelles idées. Pour cette étude, Isaac Newton cherche à modéliser l’idée de variable à l’aide du concept de temps, qu’il appelle fluente : « J'appellerai quantité fluente, ou simplement fluente, ces quantités que je considère comme augmentées graduellement et indéfiniment, et je les représenterai par les dernières lettres de l’alphabet v, x, y et z ».

Vu sous l’angle de la théorie des équations, cela revient à remplacer le X des formules utilisées depuis Diophante, par un x qui devient une quantité qui varie de moins à plus l’infini. Le polynôme devient une fonction et à ce titre jouit de nouvelles propriétés. Les outils associés au calcul infinitésimal sont la limite, la dérivée ou encore l’intégrale. En 1691, Michel Rolle les utilise pour établir un théorème, indiquant que si a et b sont deux racines d’un polynôme P non constamment nul, il existe une valeur c comprise dans l’intervalle ]a, b[racine du polynôme dérivée de P, retrouvant un résultat de Bhaskara II et Sharaf al-Dîn al-Tûsîau du XII^e siècle. Une autre application est une découverte de Newton pour le calcul des racines, appelée méthode de Newton. Elle consiste à choisir initialement une valeur, à calculer la tangente du polynôme en cette valeur, à trouver la racine de la tangente et à réitérer.

Si ces résultats apportent des éléments nouveaux à la théorie des équations, ils n’en font pas partie au sens propre. Newton développe sa méthode pour les polynômes, mais elle n’est en rien spécifique à ceux-ci et permet d’approximer un zéro d’une fonction dérivable quelconque, ce dont Newton prend conscience puisqu’il applique ensuite sa méthode à des fonctions non polynomiales. Le théorème de Rolle est maintenant généralisé à toute fonction dérivable, même si la démonstration de ce résultat date de 1860. D’autres résultats de même nature, comme la méthode de Ruffini-Horner pour approximer une racine ou le théorème de Sturm pour localiser la présence d’une solution dans un intervalle, sont mis au point durant le XIX^e siècle.

Imaginaires et nombres complexes

Les travaux de Leonhard Euler sont à l’origine d’une meilleure compréhension des nombres complexes, indispensable à la théorie des équations.

Les nombres imaginaires sont nés dans une ambiguïté que le calcul infinitésimal finit par dissiper. Pour Bombelli, un nombre imaginaire est une longueur géométrique à laquelle on a ajouté l’un des quatre signes possibles : le plus des vraies longueurs, le moins, ainsi que deux autres qu’il appelle piu di meno et meno di meno qui correspondent avec nos notations à i et -i. Il existe une autre définition, plus générale mais plus vague, qui nous vient de Descartes. Il utilise pour la première fois le terme imaginaire en 1637. Pour exprimer les relations entre les coefficients et les racines, mises en évidence par Viète, il est nécessaire de faire parfois appel à des nombres impossibles soit parce qu’ils sont «moindres que rien» ce qui ne fait pas sens pour une longueur, soit parce qu’ils sont impossibles. Ces racines doivent alors être imaginées, elles sont « [...] quelquefois seulement imaginaires c’est-à-dire que l’on peut toujours en imaginer autant que j'ai dit en chaque équation, mais qu’il n’y a quelquefois aucune quantité qui corresponde à celle qu’on imagine ». Ces deux définitions ne semblent pas équivalentes. Dans un cas, les nombres imaginaires sont définis comme des complexes de la forme a + i.b, dans l’autre, un nombre imaginaire est n’importe quoi qui pourrait servir aux calculs intermédiaires d’une équation algébrique. A. Dahan-Dalmedico et J. Peiffer précisent décrivent ainsi cette double définition : « Dès son origine, une ambiguïté préside à l’apparition de ce terme imaginaire : entre d’une part l’acception idéale de Descartes ou même de Girard et, d’autre part, les nombres de la forme a + b√-1, avec a, b réels, qui interviennent dans les résolutions des équations de bas degré ».

Le calcul infinitésimal incite au choix d’une définition précise et permet de résoudre les paradoxes apparents de ces étranges nombres. La racine carrée possède une propriété algébrique, si a et b sont deux réels positifs, √a.√b = √a.b, d’où un premier paradoxe :

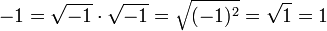
À travers des développements en série, Leibniz parvient à justifier des égalités de Bombelli comme :

Les travaux de De Moivre mettent en évidence une correspondance entre les imaginaires de Bombelli et la trigonométrie. La formule d'Euler e^iπ + 1 = 0 donne leurs lettres de noblesses aux nombres complexes de la forme a + i.b. Tobias Dantzig remarque que cette formule contient : « les symboles les plus importants : union mystérieuse dans laquelle l’arithmétique est représentée par 0 et 1, l’algèbre par √-1, la géométrie par π et l’analyse par e. » La logique de Bombelli est définitivement adoptée.

Si ces travaux ne se rattachent pas à l'algèbre ou à la théorie des équations, ils sont néanmoins indispensables pour comprendre son histoire et son contenu.

Théorème fondamental de l’algèbre

Jean le Rond d’Alembert est le premier à ressentir la nécessité de démontrer le théorème fondamental de l’algèbre.

Le récent statut acquis par ces nombres imaginaires impose la démonstration d’un théorème : Tout polynôme non constant admet au moins une racine complexe. Il est alors entendu que les coefficients sont des nombres réels. C’est Jean le Rond d’Alembert qui en exprime la première fois le besoin en 1746. Sa motivation n’est en rien algébrique, il souhaite intégrer des fonctions rationnelles et utilise pour cela une décomposition en éléments simples. Sa démonstration est issue de ses préoccupations, elle est purement analytique.

La question est immédiatement considérée comme importante, et ce résultat prend le nom de théorème fondamental de l’algèbre. Le terme est cohérent car l’algèbre désigne, à cette époque, la théorie des équations. Mais la preuve de d’Alembert ne séduit pas. Tout d’abord, elle suppose connus deux résultats, l’existence d’un minimum pour une fonction continue définie sur un compact ; ensuite un théorème de convergence de série, maintenant appelé théorème de Puiseux. L’absence de techniques topologiques et de connaissance sur la convergence rend à l’époque impossible une démonstration complète. Ensuite, l’usage exclusif de l’analyse n’apparaît pas comme la méthode la plus adéquate pour démontrer le résultat fondamental de la théorie des équations.

Euler reprend la question sous un angle algébrique, héritage d’al-Khawarizmi et de Viète. Son objectif est de montrer que les racines, au sens de Descartes, sont bien des nombres complexes au sens de Bombelli. Dans le cas du degré 4, sa démonstration est rigoureuse mais inutile, les formules de Ferrari établissant déjà le résultat. Pour les autres cas, la démonstration n’est qu’esquissée. Lagrange comble les lacunes en 1771.

Cette approche algébrique ne convainc pas Gauss qui indique : « l’hypothèse de base de la démonstration est que toute équation possède effectivement n racines possibles ou impossibles. Si l’on entend par possibles réels et par impossibles, complexes, cet axiome est inadmissible puisque c’est justement ce qu’il s’agit de démontrer. Mais si l’on entend par possibles les quantités réelles et complexes et par impossibles tout ce qui manque pour qu’on ait exactement n racines, cet axiome est acceptable. Impossible signifie alors quantité qui n’existe pas dans tout le domaine des grandeurs. » Rien ne permet effectivement encore de donner un sens comme le fait Descartes aux racines, qui sont pourtant utilisées dans les calculs de Lagrange.

La première démonstration de Gauss est construite sur le canevas de d’Alembert, mais la compréhension des fonctions continues est encore trop faible pour permette de conclure. Les travaux de Bolzano finissent par permettre à Jean-Robert Argand de rédiger la première démonstration solide, encore sur les idées de d’Alembert. Gauss trouve une preuve un peu plus tard, cette fois ci sur le canevas d’Euler et de Lagrange. Sa compréhension des polynômes formels lui permet de trouver un contournement. Comme toutes les preuves algébriques du théorème, elle contient une partie analytique, à savoir l’existence d’une racine si le degré du polynôme est impair.

L’article détaillé relate plus précisément cette partie de l’histoire et propose diverses démonstrations du théorème.