Théorie des équations (histoire des sciences) - Définition

Vers le théorème d'Abel

Premières tentatives

Si la découverte du calcul infinitésimal permet quelques percées, celles-ci ne sont guère algébriques, et à ce titre n’entrent que partiellement dans la théorie des équations. Les mathématiciens , forts des succès concernant les équations de degré inférieur à quatre, se sont efforcés de trouver des formules analogues à celles d’al-Khawarizmi, Cardano ou Ferrari, mais cette fois pour un degré quelconque. Plusieurs tentatives, émanant de Tschirnhaus (un ami de Leibniz) puis d'Euler et enfin de Bézout, se soldent par des échecs.

Les canevas sont similaires, l’objectif est de ramener une équation de degré n à une forme canonique Xⁿ - c = 0. À partir de cette forme canonique, l’équation n’est pas encore complètement résolue mais les travaux de Moivre en trigonométrie permettent d'écrire une solution x _k, si c est positif :

Pour cela, la méthode consiste à passer d’une équation à une inconnue P(X) = 0 à deux équations à deux inconnues en ajoutant la suivante : Q(X) - Y = 0. En choisissant habilement le polynôme Q, serait-il possible d’annuler les coefficients intermédiaires ? Pour n égal à 2, 3 ou même 4, cette méthode revient à résoudre une équation d’un degré inférieur, que l’on résout avec les méthodes précédentes. Mais avec n égale 5, l’équation à résoudre est de degré 120, et si l’on peut ramener son degré à 24 par d’autres artifices, la méthode n’est guère concluante.

Le point noir de la théorie reste la résolution effective de l’équation polynomiale.

Vandermonde et l’équation cyclotomique

Les racines du polynôme cyclotomique sont régulièrement espacées sur le cercle trigonométrique complexe.

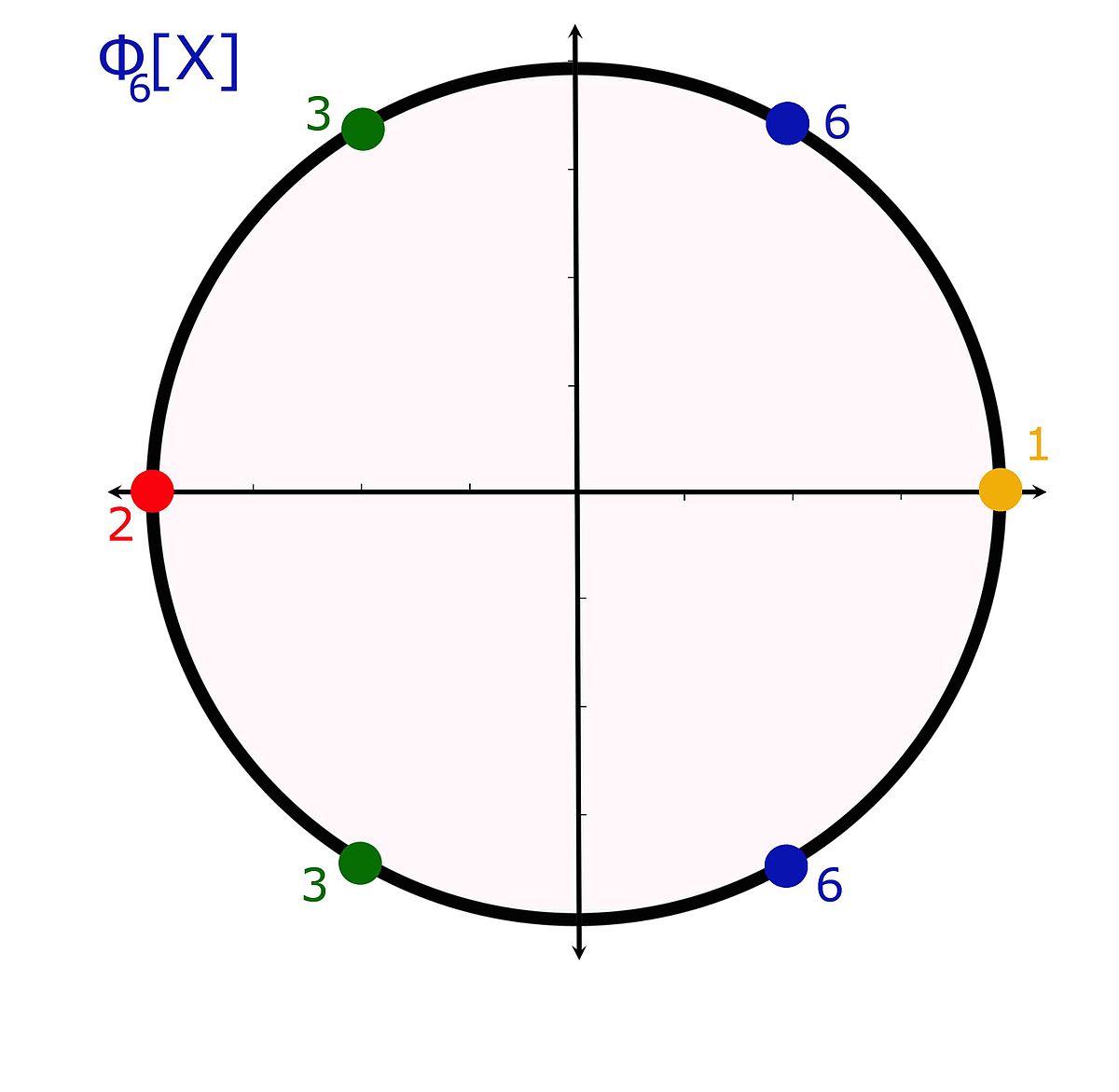
En 1771, Alexandre-Théophile Vandermonde apporte du nouveau sur ce délicat point noir. Son ambition est plus modeste que celle de ses prédécesseurs. Il ne cherche plus à résoudre l’équation algébrique dans son intégralité, mais uniquement celle que les tentatives précédentes recherchaient comme point d’arrivée, à savoir Xⁿ - c = 0. Comme le passage du coefficient 1 au coefficient c est trivial, il se limite à l’équation Xⁿ - 1 = 0, dite cyclotomique. La valeur n peut être choisie parmi les nombres premiers, la résolution de ce cas particulier permet d’en déduire les solutions dans le cas général.

Une expression trigonométrique de la solution est connue, ce qui assure que les n racines de l’équation sont bien complexes et dans ce cas particulier, le théorème fondamental de l’algèbre est déjà établi. Il reste encore à trouver une formule algébrique capable de les exprimer. Par formule algébrique, on entend une expression contenant des nombres rationnels, l’unité imaginaire i, les quatre opérations et des fonctions racines n^ièmes. Le terme consacré est résolution par radicaux de l’équation algébrique.

La méthode de Vandermonde consiste à faire usage de polynômes en plusieurs indéterminées, et particulièrement des polynômes symétriques, c’est-à-dire ceux qui sont invariants par toute permutation des indéterminées. La relation entre les coefficients et les racines peut se lire comme le fait que n polynômes symétriques à n indéterminées ont une image connue du n-uplet des racines, ces images sont les coefficients du polynôme. Ce résultat est une reformulation d’une remarque de Viète. L’intérêt est que ces n polynômes symétriques génèrent l’intégralité des polynômes symétriques. En plus les images sont particulièrement simples pour le polynôme cyclotomique, elles sont toutes nulles, à l’exception de celle associée au polynôme X₁...X_n, qui vaut ±1 selon la parité de n. Enfin, si les racines sont notées dans l’ordre trigonométrique ξ₀ = 1, ξ₁, ξ₂,..., ξ_n on trouve que, ξ_j.ξ_k = ξ_j+k si j + k < n, et ξ_n-j-k sinon.

La méthode de Vandermonde consiste à calculer des sommes partielles de racines, qui peuvent s’exprimer comme des images de fonctions rationnelles en des polynômes symétriques. Ceci permettrait de calculer ses sommes partielles, puis d’appliquer une nouvelle décomposition de chaque somme en sous-sommes et de calculer ces sous-sommes. En réitérant, il a l’espoir d’obtenir des sous-sommes composées chacune d’une unique racine et de conclure. Cette méthode lui permet de résoudre le cas où n est égal à 11, mais une méthode générique reste hors de portée. Il a toutefois résolu une équation du 11^e degré qui n’avait aucune factorisation évidente autre que celle associé au terme (X - 1).

Pour résoudre l’équation cyclotomique de degré quelconque, il reste encore un problème combinatoire. Comment associer les racines pour en faire des sommes partielles, solutions d’équations de degrés moindres ? Problème que ne résout pas Vandermonde. L’article détaillé propose une résolution pour les degrés 5 et 17.

Synthèse de Lagrange

Lagrange remet sérieusement en doute la possibilité de résolution algébrique de l’équation, dans le cas général.

Dans son mémoire de 1771, Lagrange réalise une synthèse de toutes les méthodes utilisées dans le passé pour résoudre l’équation algébrique de petit degré. À l’aide de cette synthèse, il développe une méthode, qui s’applique aux degrés 2, 3 et 4. Il montre de plus que cette méthode ne peut aboutir dans le cas général si le degré est plus élevé. Sa démarche, même si elle aboutit à un échec, est à beaucoup d’égards un véritable pas en avant.

Tout d’abord, la méthode est suffisamment générale pour que toutes les tentatives précédentes ne soient que des cas particuliers de la sienne. Il met ainsi un terme à l’époque des méthodes empiriques de Tschirnchaus ou Euler, nécessairement vouées à l’échec.

Il reprend l’idée de Vandermonde d’utiliser les fonctions symétriques ainsi que les relations entre les coefficients et les racines et montre l’importance des n! permutations des racines pour la résolution du cas général. Il établit à ce propos deux théorèmes préfigurant la théorie des groupes. Le premier est que les n! permutations d’un n-uplets ont comme image par une fonction de n variables un ensemble de cardinal un diviseur de n!. Ce résultat est un ancêtre de ce que l’on appelle maintenant le théorème de Lagrange sur les groupes. Le deuxième concerne les fonctions qu’il qualifie de semblables et qui sont invariantes par le même sous-groupe de permutation. Ce résultat anticipe les théorèmes sur les suites de sous-groupes que l’on trouve dans la théorie de Galois ou dans le Théorème de Jordan-Hölder. La conclusion de Lagrange est pessimiste : « d’où il s’ensuit que, si la résolution algébrique des équations de degrés supérieurs au quatrième n’est pas impossible, elle doit dépendre [...] » L’idée d’une impossibilité de résolution algébrique de l’équation est émise. Le chemin est tracé, soit pour trouver une méthode générale de résolution, soit pour montrer l’inexistence d’une telle méthode. La solution réside dans une analyse combinatoire des possibles permutations des racines. La conclusion est analogue à celle de Vandermonde pour le polynôme cyclotomique, mais cette fois, elle valable dans le cas général.

En parallèle des travaux de Vandermonde et de Lagrange, les développements de l’analyse ont fait perdre beaucoup d’intérêt au problème millénaire de la résolution d’une équation. À l’époque des mathématiques arabes, cette résolution était une méthode de calcul numérique essentielle. Al-Buruni souhaitait résoudre l’équation cubique pour calculer des sinus de tiers d’angle déjà connue. Dès l’aube du XIX^e siècle, l’analyse offre des méthodes beaucoup plus efficaces pour calculer des racines. Les résultats de Lagrange montrent qu’il faudra de plus, soit beaucoup de calculs, soit une grande idée, pour mettre un point final à cette question. De plus, elle risque fort de prendre la forme d’un constat d'échec, peu prometteur en termes de progrès des mathématiques. Cet environnement n’est pas favorable pour motiver des mathématiciens déjà renommés par ailleurs.

Progrès de Gauss

Carl Friedrich Gauss pousse plus loin les travaux initiés par Vanermonde sur les polynômes cyclotomiques. Il use pour cela d’une approche structurelle, qui préfigure l’avenir de l’algèbre.

Gauss ouvre le siècle suivant en apportant des éléments de réponses, sur les questions de Vandermonde et de Lagrange. Avancer dans la théorie des équations suppose le choix de bonnes fonctions rationnelles, invariantes par certaines permutations des racines. Lagrange l’a clairement montré et Vandermonde a émis l’hypothèse qu’elles devaient exister pour l’équation cyclotomique. Le nombre de permutations augmente rapidement en fonction du degré n du polynôme, il en existe factorielle n, soit déjà 120 pour le degré 5. L’approche aléatoire imposerait une quantité de calcul rapidement rédhibitoire. Gauss tient compte de cet acquis et change radicalement les méthodes d’analyse.

Il ne s’attaque pas au problème général, mais uniquement à l’équation cyclotomique, qu’il appelle « la théorie de la division du cercle ». Sa méthode préfigure la démarche-clé du XIX^e siècle, toujours en vigueur. Au lieu d’étudier directement le polynôme, il analyse la structure de l’ensemble des polynômes muni de son addition et de sa multiplication. Cette structure possède des points communs avec celle des entiers, il en conclut que cette branche des mathématiques « n’appartient pas par elle-même à l’arithmétique, mais ses principes ne peuvent être puisés que dans l’arithmétique transcendante. Ce résultat pourra sembler aux géomètres aussi inattendu que les vérités nouvelles qui en dérivent ». Par arithmétique transcendante, Gauss entend ce que l’on appelle maintenant la théorie algébrique des nombres. En termes contemporains, l’analogie provient du fait que si les coefficients sont choisis dans un corps commutatif, l’anneau des polynômes et celui des entiers sont tous les deux euclidiens. Il va considérer les ensembles de polynômes en choisissant les coefficients les plus divers. Le cas où ils sont entiers l’amène à démontrer un lemme qui porte son nom, montrant le caractère factoriel de cette structure. Il utilise une de ses découvertes, l’arithmétique modulaire et travaille aussi sur des polynômes à coefficients sur les corps finis. Cette démarche impose l’usage du polynôme formel au détriment de la fonction polynôme, remettant ainsi à l’honneur la conception de Viète du polynôme.

Pour choisir les bonnes permutations, Gauss remarque qu’elles sont liées à la structure du groupe multiplicatif des racines, ou plus exactement celui de ses automorphismes. Dans le cas du polynôme cyclotomique, les racines sont les racines n^ièmes de l’unité et elles forment un groupe commutatif. À la différence de Lagrange, il perçoit l’importance de la loi du groupe, qui permet de combiner les différents éléments, alors que Lagrange se limitait à un simple dénombrement. Cette opération se traduit par des sommes de Gauss, qui permettent de trouver les sommes partielles imaginées par Vandermonde. Il en profite pour résoudre une conjecture qu’avaient vainement tenté de démontrer Euler et Legendre : la loi de réciprocité quadratique.

Si Gauss fait progresser la théorie des équations, son objectif est néanmoins différent ; il met à jour une connexion inattendue entre la théorie des nombres et celle des équations.

Solution d'Abel

Niels Henrik Abel montre l’impossibilité de la résolution par radicaux de l’équation algébrique, dans le cas général, mettant fin à la quête millénaire et centrale de la théorie des équations. Son résultat est passé sous silence.

L’éventuelle impossibilité de la résolution par radicaux du cas général fait son chemin. Paolo Ruffini publie quatre mémoires à ce sujet, en 1799, 1804 puis en 1808 et 1813. Pour la première fois, est déclarée clairement cette impossibilité. Sa tentative pour le montrer suit la démarche de Lagrange et consiste à montrer que l’usage d’une équation auxiliaire ne permet pas, pour le degré 5, d’abaisser systématiquement le degré de l’équation initiale. Il établit que, si une fonction symétrique de cinq variables prend strictement moins de cinq valeurs par permutations des variables, alors elle n’en prend pas plus de 2. En conséquence, si la méthode de Tschirnhaus fonctionnait, elle réduirait une équation du cinquième degré à une équation du deuxième degré, ce qui n’est pas possible dans le cas général. Cette approche est lacunaire. Rien n’indique qu’une approche radicalement différente de celles décrites par Lagrange ne pourrait aboutir.

Pour conclure de manière définitive, il fallait raisonner différemment que ne l’avaient fait Lagrange ou Ruffini. Niels Abel l’exprime ainsi : « [...] on se proposait de résoudre les équations sans savoir si cela était possible. Dans ce cas, on pouvait bien parvenir à la résolution, quoique ce ne fût nullement certain [...] Au lieu de demander une relation dont on ne sait pas si elle existe ou non, il faut se demander si une telle relation est en effet possible. » En 1826, Abel part du résultat et suppose qu’il existe une formule, fonction rationnelle de radicaux, qui donne la solution d’une équation de degré 5. Il sait qu’elle est à même d’exprimer 5 racines différentes et qu’en conséquence, elle possède un comportement précis vis à vis des permutations des variables, déjà étudiées par Vandermonde, Lagrange puis Cauchy. Il démontre que ce comportement introduit une absurdité.

Ce résultat reste à ce moment fort peu connu. Son article, pourtant envoyé à Gauss, Legendre et Cauchy n’intéresse personne. Gauss, qu’Abel souhait rencontrer dans sa ville de Göttingen, ne le reçoit pas. D’un point de vue théorique, le résultat d’Abel apparaît tout d’abord comme la mort de la théorie des équations, du moins sous sa forme classique, et l’intérêt de s’investir dans une branche condamnée semble limité. Et puis, à quoi bon souhaiter exprimer les racines sous forme de radicaux ? En termes algébriques, comme le fait remarquer Gauss, il est plus simple de noter les racines x₁,..., x_n et l’expression sous forme de radicaux est un peu désuète. En termes de calcul numérique, cette méthode est lourde, comparée à ce que permet l’analyse. Il suffit, pour s’en rendre compte, de regarder l’expression de la partie réelle d’une des racines de l’équation X ¹⁷ - 1 = 0, trouvée par Gauss :

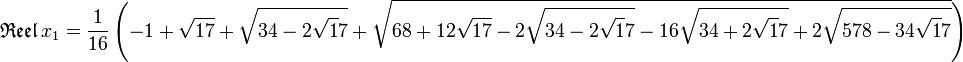
Abel ne trouve une première notoriété que posthume, avec son travail sur les intégrales elliptiques, et non avec son travail sur la théorie des équations.