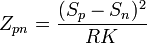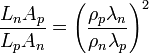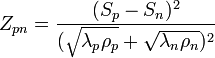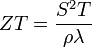Thermoélectricité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Découvert puis compris au cours du XIXe siècle grâce aux travaux de Seebeck, Peltier ou encore Lord Kelvin, l'effet thermoélectrique est un phénomène physique présent dans certains matériaux : il y lie le flux de chaleur qui les traverse au courant électrique qui les parcourt. Cet effet est à la base d'applications de réfrigération (ex. module Peltier) et de génération d'électricité : un matériau thermoélectrique va permettre de transformer directement de la chaleur en électricité, ou de déplacer des calories par l'application d'un courant électrique.
Un grand nombre des matériaux possédant des propriétés thermoélectriques intéressantes ont été découverts au cours des décennies 1950 et 1960. C'est notamment le cas du tellurure de bismuth (Bi2Te3) utilisé dans les modules Peltier commerciaux, ou des alliages silicium-germanium (SiGe) utilisés pour l'alimentation des sondes spatiales dans des générateurs thermoélectriques à radioisotope.
Jusqu'à présent, les rendements peu élevés et les coûts importants des systèmes de conversion thermoélectriques les ont limités à un marché de niche. Néanmoins, des progrès récents ainsi qu'un nouvel intérêt pour ces systèmes, dû à la fois à la hausse des coûts de l'énergie et aux exigences environnementales, ont conduit à un renouveau important des recherches scientifiques dédiées à cette technologie (voir par exemple).
Aspects historiques
Le premier effet thermoélectrique a été découvert par le physicien allemand Thomas Johann Seebeck en 1821. Celui-ci remarqua qu’une aiguille métallique est déviée lorsqu’elle est placée entre deux conducteurs de natures différentes liés par des jonctions à leurs extrémités et soumis à un gradient thermique (voir effet Seebeck). Il interprète ses observations en postulant un lien entre champ magnétique et différence de température entre les deux jonctions et établit le sens de déviation de l'aiguille pour un grand nombre de couples. Il pense ainsi avoir trouvé une explication à l'origine du champ magnétique terrestre. En réalité, l'effet observé est d'origine électrique : une différence de potentiel apparaît à la jonction de deux matériaux soumis à une différence de température. L’utilisation la plus connue de l’effet Seebeck est la mesure de température à l’aide de thermocouples.
Quelques années plus tard, en 1834, le physicien français Jean Peltier découvrit le second effet thermoélectrique : une différence de température apparaît aux jonctions de deux matériaux de natures différentes soumis à un courant électrique (voir effet Peltier). En 1838, Heinrich Lenz montre que de la chaleur est absorbée ou libérée à une jonction suivant le sens du courant.
Le physicien anglais William Thomson (Lord Kelvin) montra en 1851 que les effets Seebeck et Peltier sont liés : un matériau soumis à un gradient thermique et parcouru par un courant électrique échange de la chaleur avec le milieu extérieur. Réciproquement, un courant électrique est généré par un matériau soumis à un gradient thermique et parcouru par un flux de chaleur. La différence fondamentale entre les effets Seebeck et Peltier considérés séparément et l’effet Thomson est l'existence de ce dernier pour un seul matériau et l'inutilité d’une jonction (voir effet Thomson).
Principes de base, en détails
La conversion d'énergie par effet thermoélectrique (chaleur → électricité ou électricité → chaleur) est basée à la fois sur les effets Seebeck, Peltier et Thomson.
Bref rappel sur les coefficients Seebeck, Peltier et Thomson
Coefficient Seebeck
Une différence de température dT entre les jonctions de deux matériaux a et b implique une différence de potentiel électrique dV selon :
Le coefficient Seebeck, également appelé « Pouvoir Thermoélectrique » s'exprime en V.K-1 (ou plus généralement en µV.K-1 au vu des valeurs de ce coefficient dans les matériaux usuels).
Les coefficients Seebeck des deux matériaux sont reliés au coefficient Seebeck du couple selon :
Coefficient Peltier
Dans le cas de l’effet Peltier, un courant électrique I est imposé à un circuit composé de deux matériaux, ce qui entraîne une libération de chaleur Q à une jonction et une absorption de chaleur à l’autre jonction, selon :
Coefficient Thomson
Au contraire des coefficients Seebeck et Peltier, le coefficient Thomson peut être défini directement pour un seul matériau. Lorsque sont présents simultanément un gradient de température et un courant électrique, il y a génération ou absorption de chaleur dans chaque segment de matériau pris individuellement. Le gradient de flux thermique au sein du matériau est alors donné par :
où x est la coordonnée spatiale et τ est le coefficient Thomson du matériau.
Relations entre les coefficients Seebeck, Peltier et Thomson
Kelvin a montré que les trois coefficients Seebeck, Peltier et Thomson ne sont pas indépendants les uns des autres. Ils sont liés par les deux relations :
Principes de la conversion d'énergie par effet thermoélectrique
Pour la réfrigération ou la génération d’électricité par effet thermoélectrique, un « module » est constitué de « couples » connectés électriquement. Chacun des couples est constitué d’un matériau semi-conducteur de type p (S>0) et d’un matériau semi-conducteur de type n (S<0). Ces deux matériaux sont joints par un matériau conducteur dont le pouvoir thermoélectrique est supposé nul. Les deux branches (p et n) du couple et tous les autres couples composant le module sont connectés en série électriquement et en parallèle thermiquement (voir schéma à droite). Cette disposition permet d’optimiser le flux thermique qui traverse le module et sa résistance électrique. Par souci de simplicité, nous raisonnerons dans la suite sur un seul couple, formé de deux matériaux de sections constantes.
La figure à droite présente le schéma de principe d’un couple p-n utilisé pour la réfrigération thermoélectrique. Le courant électrique est imposé de telle manière que les porteurs de charge (électrons et trous) se déplacent de la source froide à la source chaude (au sens thermodynamique) dans les deux branches du couple. Ce faisant, ils contribuent à un transfert d’entropie de la source froide à la source chaude, et donc à un flux thermique qui va s’opposer à celui de la conduction thermique. Si les matériaux choisis ont de bonnes propriétés thermoélectriques (nous verrons par la suite quels sont les paramètres importants), ce flux thermique créé par le mouvement des porteurs de charge sera plus important que celui de la conductivité thermique. Le système permettra donc d'évacuer de la chaleur depuis la source froide vers la source chaude, et agira alors comme un réfrigérateur.
Dans le cas de la génération d'électricité, c'est le flux de chaleur qui entraîne un déplacement des porteurs de charge et donc l'apparition d'un courant électrique.
Rendement de conversion et paramètres importants
Calcul du rendement de conversion d'un système thermoélectrique
Le calcul du rendement de conversion d'un système thermoélectrique s'effectue en déterminant la relation entre le flux de chaleur et le courant électrique dans le matériau. Il nécessite l'utilisation des relations de Seebeck, Peltier et Thomson (voir plus haut), mais aussi des lois de propagation de la chaleur et du courant électrique.
L'exemple suivant présente le calcul du rendement de conversion dans le cas de la réfrigération (celui de la génération d'électricité peut être effectué par des raisonnements analogues).
Reprenons donc le schéma précédent. Dans chacune des deux branches du couple, le flux de chaleur généré par l’effet Peltier s’oppose à la conductivité thermique. Les flux totaux sont donc dans la branche p et la branche n :
-
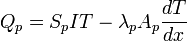
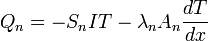
avec x la coordonnées spatiale (voir schéma), λp et λn les conductivités thermiques des matériaux, et Ap et An leurs sections.
La chaleur est donc extraite de la source froide avec un flux Qf :
Dans le même temps, le courant qui parcourt les deux branches est à l’origine d’une création de chaleur par effet Joule I2ρ/A par unité de longueur des branches. En utilisant l’équation de Domenicali et en supposant que le coefficient Thomson est nul (cela revient à supposer que S est indépendant de la température, voir la relation de Thomson), la conservation de l’énergie dans le système s’écrit dans les deux branches :
-
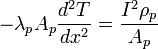
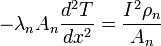
En considérant des conditions aux limites T=Tf en x=0 et T=Tc en x=Lp ou x=Ln avec Lp et Ln les longueurs des branches p et n, Tf et Tc les températures des sources froide et chaude, Qf s'écrit :
avec K et R les conductance thermique et résistance électrique totales des branches du couple :
-
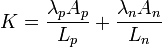
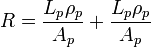
La puissance électrique W fournie au couple correspond à l’effet Joule et à l’effet Seebeck, soit :
Le rendement du système de réfrigération thermoélectrique correspond au rapport de la chaleur extraite de la source froide à la puissance électrique dissipée, soit :
Pour une différence de température ΔT donnée, le rendement dépend du courant électrique imposé. Deux valeurs particulières du courant permettent de maximiser soit le rendement de conversion η soit la chaleur extraite de la source froide Q_f.
Par un raisonnement similaire, le rendement d’un couple p-n utilisé en génération d’électricité sera donné par le rapport de la puissance électrique utile délivrée à une résistance de charge r au flux thermique traversant le matériau :
Ici encore, deux valeurs particulières de I maximisent soit le rendement de conversion soit la puissance électrique délivrée par le système.
Paramètres importants pour obtenir un bon rendement
En maximisant ces deux rendements de conversion, on peut montrer qu’ils dépendent uniquement des températures Tf et Tc et d'une grandeur adimensionnelle ZpnTM appelée « facteur de mérite » (TM est la température moyenne du système, TM=(Tf+Tc)/2) dont l'expression est :
On remarque que Zpn pour un couple n’est pas une quantité intrinsèque au matériau mais dépend des dimensions relatives des branches du module au travers de R et K (résistance électrique et conductance thermique). Le rendement de conversion du système (en génération d'électricité comme en refroidissement) est maximum lorsque Zpn est maximum, donc lorsque le produit RK est minimum, ce qui est vérifié quand :
Le facteur de mérite Zpn devient alors fonction uniquement de paramètres intrinsèques aux matériaux :
Pour obtenir un rendement de conversion maximum, il convient donc de choisir les matériaux constituant le couple de manière à maximiser Zpn. En règle générale, cela ne revient pas simplement à optimiser individuellement les deux matériaux pour optimiser leurs facteurs de mérite respectifs Z=S2/(ρλ). À la plupart des températures utilisées dans la pratique, et notamment celles utilisées pour la génération d’électricité, les propriétés thermoélectriques des meilleurs matériaux de type p et de type n sont similaires. Dans ce cas, le facteur de mérite du couple est proche de la moyenne des facteurs de mérite individuels, et il est raisonnable d’optimiser les deux matériaux indépendamment l’un de l’autre.
L’optimisation de matériaux pour une utilisation dans la conversion d’énergie par effet thermoélectrique passe donc nécessairement par l’optimisation de leurs propriétés de transport électriques et thermiques de manière à maximiser le facteur de mérite :
Un bon matériau thermoélectrique possèdera donc simultanément un coefficient Seebeck élevé, une bonne conductivité électrique (c.-à-d. une faible résistance électrique) , et une faible conductivité thermique.
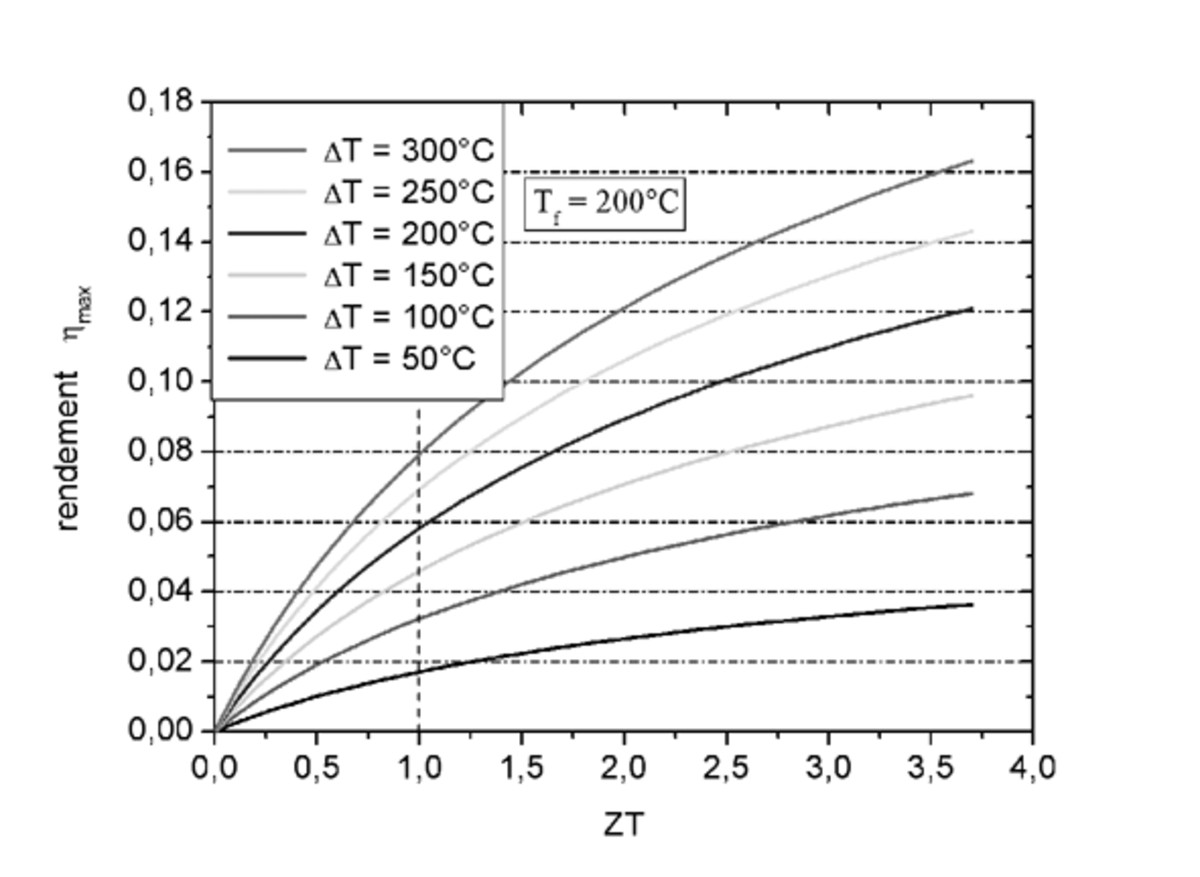
La figure ci-contre montre l'évolution du rendement de conversion d'un système thermoélectrique dans des conditions idéales en fonction du facteur de mérite ZT. Par exemple, si ZT=1 et que la différence de température est de 300 °C, le rendement de conversion sera de 8 %, ce qui signifie suivant le cas (génération d'électricité ou réfrigération) que 8 % de la chaleur traversant le matériau sera convertie en électricité, ou bien que la chaleur extraite par le refroidissement correspondra à 8 % de la puissance électrique employée.
Modules thermoélectriques
Optimisation géométrique
Nous avons vu que les propriétés de conversion d'un couple de matériaux thermoélectriques constituant un module ne sont pas uniquement intrinsèques : elles dépendent également de la géométrie du système (longueur et section des branches du module) dont dépendent la résistance électrique R et la conductance thermique K des branches. Il faut en effet que K soit suffisamment faible pour qu'un gradient thermique puisse être maintenu, tout en étant suffisamment élevée pour que de la chaleur traverse le module : si K est nulle aucune chaleur ne traverse le module et il n'y a donc pas de conversion. De même, R doit être choisie de manière à avoir le meilleur compromis possible entre la puissance électrique et la différence de potentiel électrique. Une fois les matériaux constituant le module choisis (grâce au facteur de mérite ZT), il est donc nécessaire d'optimiser la géométrie du système pour pouvoir obtenir le rendement de conversion, la puissance électrique ou la chaleur extraite maximum en fonction de l'application du module.
Modules segmentés
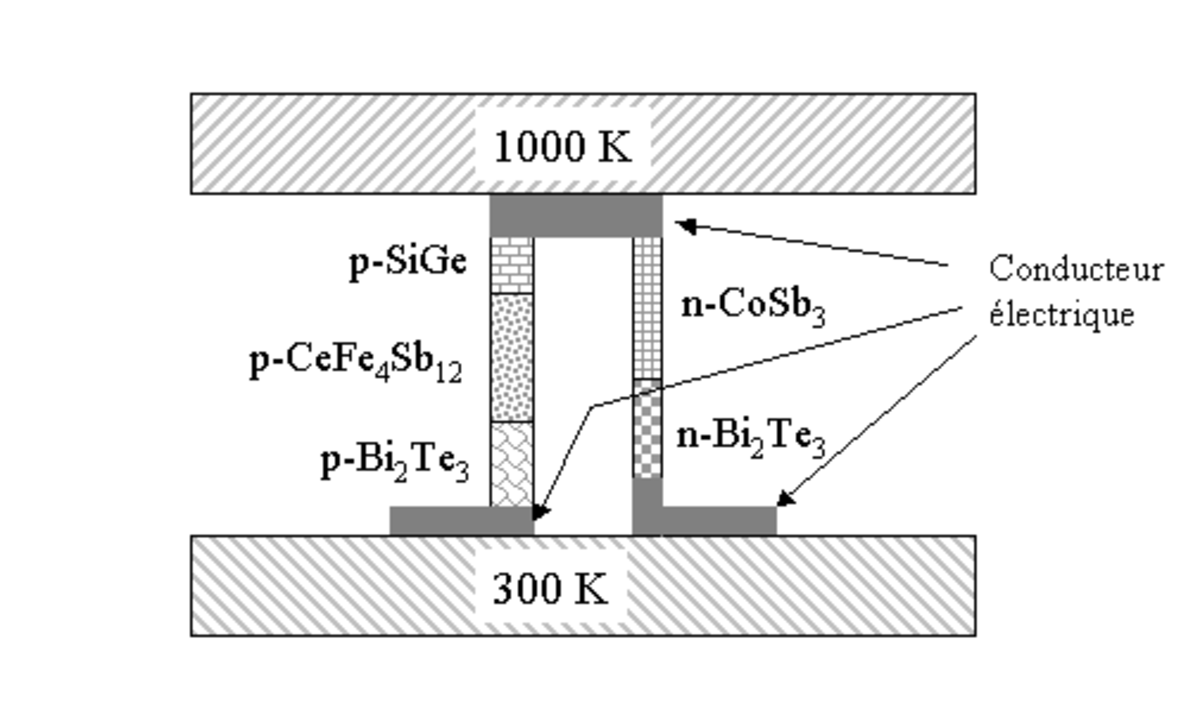
Les matériaux utilisés dans les modules de conversion thermoélectrique ne sont généralement efficaces que dans une gamme de température restreinte. Ainsi, l'alliage SiGe utilisé pour l'alimentation de la sonde Voyager n'est efficace qu'à des températures supérieures à 1 000 K environ. Il peut donc être intéressant, pour des applications où le gradient de température est très grand, d'utiliser plusieurs matériaux thermoélectriques dans chaque branche, chacun dans la gamme de température pour laquelle il est le plus efficace. On parle alors de module thermoélectrique segmenté.
La figure ci-contre illustre le concept de module thermoélectrique segmenté. Nous avons ici un gradient de température très important (700 K de différence entre la zone chaude et la zone froide), et aucun matériau connu n'est efficace dans toute la gamme de température. Chacune des deux branches du couple est donc formée de plusieurs matériaux (ici deux pour la branche n et trois pour la branche p). La longueur de chacun de ces matériaux est choisie pour qu'il soit utilisé dans la gamme de température où il est le plus efficace. Un tel module permettra donc d'obtenir un rendement de conversion, une puissance électrique, ou une chaleur extraite, nettement plus élevée que si chaque branche n'était composée que d'un seul matériau. Ainsi, les meilleurs rendements obtenus en laboratoire avec ce type de modules sont à l'heure actuelle voisins de 15 % (ce qui signifie que 15 % de la chaleur traversant le matériau est convertie en puissance électrique). Les modules segmentés sont cependant d'un prix beaucoup plus élevé que les modules « simples », ce qui les restreint à des applications pour lesquelles le coût n'est pas le facteur de choix décisif.
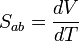
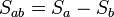
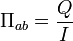
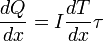
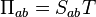
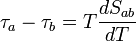
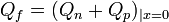
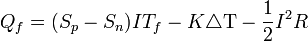
![W=I[(S_p-S_n)\triangle\mathrm{T}+IR]\,](https://static.techno-science.net/illustration/Definitions/autres/9/9075f8c4c47f477cbb799cda608de6da_ea11492a5e57cc8c79dac0decc3a0d71.png)
![\eta=\frac{Q_f}{W}=\frac{(S_p-S_n)IT_f-K\triangle\mathrm{T}-\frac{1}{2}RI^2}{I[(S_p-S_n)\triangle\mathrm{T}+IR]}\,](https://static.techno-science.net/illustration/Definitions/autres/1/1e55063740168a13181d276f33b66965_fc312fbcf3789a72abd407fb8a345711.png)
![\eta=\frac{P_u}{Q_c}=\frac{I[(S_p-S_n)\triangle\mathrm{T}-IR]}{(S_p-S_n)IT_c+K\triangle\mathrm{T}-\frac{1}{2}(R+r)I^2}\,](https://static.techno-science.net/illustration/Definitions/autres/f/f38084e764d75441a6b5de4a5305e141_24de2bd782eeeb81a845ccae98862fc6.png)