Topologie d'un espace vectoriel de dimension finie - Définition

Introduction

En mathématiques, la topologie d'un espace vectoriel de dimension finie sur un corps K est, sous certaines hypothèses, un cas particulier de topologie d'espace vectoriel normé. Le prototype est Rⁿ muni de la norme qui à un n-uplet de réels associe la plus grande des valeurs absolues de ces n réels.

Propriétés liées à la topologie du corps

Un espace vectoriel E de dimension finie n sur un corps K (par exemple sur K=le corps R des réels) peut toujours être identifié à Kⁿ par le choix arbitraire d'un isomorphisme entre ces deux espaces vectoriels (ou, ce qui est équivalent, par le choix d'une base de E). Tous les énoncés ci-dessous concernant Kⁿ s'étendent ipso facto à un tel E (muni de la topologie transportée de celle de Kⁿ par un tel isomorphisme).

Ici, le corps K considéré sera principalement celui des réels ou des complexes, corps pour lesquels toutes les hypothèses mentionnées sont vérifiées. Par conséquent, en première lecture, on peut remplacer dans tout ce qui suit K par R ou C. On peut de plus remplacer partout espace vectoriel topologique par espace vectoriel normé, qui est une notion moins générale.

Les principaux résultats seront : sur Rⁿ et Cⁿ, toutes les normes sont équivalentes ; pour l'une quelconque de ces normes, l'espace est complet (donc fermé dans tout espace vectoriel normé dont il est un sous-espace), et les parties compactes sont les fermés bornés.

Topologie produit

Si K est (comme le sont R et C) un corps topologique séparé, Kⁿ est naturellement muni d'une topologie produit (séparée) qui en fait un espace vectoriel topologique (c'est-à-dire que l'addition et la multiplication par un scalaire sont deux applications continues).

Remarquons dès à présent que si K est complet (respectivement : localement compact) alors Kⁿ le sera aussi.

Par définition de la topologie produit, on a également:

Les applications (multi-)linéaires définies sur Kⁿ sont continues, en particulier le produit scalaire, toutes les formes bilinéaires ou quadratiques, le déterminant ou encore le produit tensoriel :

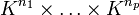
En effet, la continuité d'une application linéaire sur Kⁿ découle immédiatement du fait que E est un espace vectoriel topologique, et l'uniforme continuité est alors automatique (comme pour tout morphisme continu de groupes topologiques). Quant à la continuité d'une application p-linéaire, elle s'en déduit, par composition avec l'application p-linéaire canonique de de dans Kⁿ pour n= le produit des n_k : cette dernière est continue d'après la proposition précédente, car ses composantes sont polynômiales.

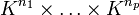
Si de plus la topologie sur K provient (comme pour R et C) d'une valeur absolue, cette topologie produit sur Kⁿ est induite par une norme : cette norme, nommée norme infini, associe à un vecteur la plus grande des valeurs absolues de ses coordonnées. Elle fait de Kⁿ un espace vectoriel normé.

Unicité de la topologie, équivalence des normes

On suppose ici que K est (comme R et C) un "corps valué" (au sens : muni d'une valeur absolue) complet, non discret. La situation est alors remarquablement simple : la topologie produit sur Kⁿ est en fait "la seule raisonnable".

Remarque : la condition de séparation est indispensable. On déduit en effet facilement de ce théorème que les topologies sur E (la séparée et les autres) compatibles avec les deux opérations sont en bijection avec les sous-espaces vectoriels de E (la séparée correspondant au sous-espace nul, et la grossière au sous-espace E).

Sur un K-espace vectoriel, toute norme induit une structure d'espace vectoriel topologique séparé. Deux normes sont équivalentes si et seulement si elles induisent la même topologie. On déduit donc immédiatement du théorème précédent :

En conséquence, il n'existe qu'un K-espace vectoriel normé de dimension n, à isomorphisme bi-uniformément continu près.

Remarque : le théorème et le corollaire ci-dessus se démontrent classiquement pour K=R, par des arguments de compacité qui sont en fait superflus : K peut ne pas être localement compact. La complétude du corps, par contre, est indispensable : par exemple l'espace vectoriel (de dimension 2, sur le corps des rationnels) est pourvu de multiples normes non équivalentes, comme N(x,y) = max( | x | , | y | ) et .

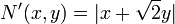
Complétude et fermeture

De cette "unicité" de la topologie (en particulier, de l'unicité de la norme à équivalence près), jointe à la complétude de Kⁿ mentionnée précédemment, on déduit un corollaire très utile en analyse fonctionnelle :

On utilise pour cela que toute partie complète d'un espace séparé est fermée (ce qui est bien connu dans le cadre métrique mais s'étend au cadre uniforme), et (pour passer des sous-espaces vectoriels aux sous-espaces affines) que toute translation est un homéomorphisme.

Les K-espaces vectoriels normés de dimension finie étant ici complets, et l'espace des applications linéaires continues à valeurs dans un complet héritant de cette complétude (propriété démontrée dans l'article Espace vectoriel normé), on en déduit un autre résultat sur la complétude :

Compacité locale

Ajoutons l'hypothèse (encore vérifiée par R et C) que le corps K ("valué" et non discret) est non seulement complet, mais même localement compact. On obtient alors la généralisation naturelle du théorème de Borel-Lebesgue :

Cette propriété n'est vraie que si E est de dimension finie. Dans le cas contraire, la boule unité fermée n'est pas compacte : ce résultat est connu sous le nom de théorème de Riesz.