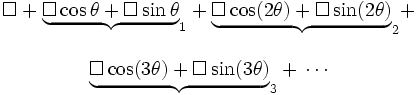Applications de la trigonométrie - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Domaines auxquels la trigonométrie s'applique - Séries de Fourier - Interaction de ces domaines avec la trigonométrie - Statistiques - Les transformations de Fourier - Théorie des nombres - Une simple expérience avec des lunettes polarisées - Exponentielles complexes

Introduction

La trigonométrie a de nombreuses applications très variées. Les applications mentionnées explicitement dans les manuels et les cours sur la trigonométrie sont souvent des utilisations pratiques, notamment en navigation, pour l'orientation, pour l'arpentage, pour la construction d'édifices, ... Elle est également employée dans certains domaines d'étude ou de recherche, principalement en mathématiques, en physique et en technologie. Dans l'esprit des gens, non mathématiciens ou non scientifiques, la trigonométrie est connue principalement pour ses applications aux problèmes de mesure, cependant elle est aussi souvent employée dans des matières insoupçonnées comme en théorie de la musique ou en théorie des nombres de manière encore plus technique. Les branches des mathématiques de l'étude des séries de Fourier et des transformations de Fourier, comptant fortement sur la connaissance des fonctions trigonométriques, trouvent des applications dans un certain nombre de secteurs, incluant les statistiques.

Domaines auxquels la trigonométrie s'applique

Les domaines scientifiques utilisant la trigonométrie sont:

l'acoustique, l'architecture, l'astronomie (et ainsi la navigation, sur les océans, dans les airs et dans l'espace; à cet égard vous pouvez voir la distance du grand cercle), la biologie, la cartographie, la chimie, le génie civil, l'infographie, la géophysique, la cristallographie, les sciences économiques (en particulier dans l'étude des marchés financiers), l'électrotechnique, l'électronique, la topographie et la géodésie, beaucoup de sciences physiques, la construction mécanique, l'imagerie médicale (tomographie axiale calculée et ultrasons), la météorologie, la théorie de la musique, la théorie des nombres (et par conséquent la cryptographie), l'océanographie, l'optique, la pharmacologie, la phonétique, la théorie des probabilités, la psychologie, la séismologie, les statistiques, et la perception visuelle.

Séries de Fourier

Beaucoup de domaine se servent de la trigonométrie d'une manière si avancée qu'il est impossible d'en discuter dans un simple article. Souvent ces utilisations font intervenir des outils appelés série de Fourier, et qui portent le nom du mathématicien et physicien français du 18ième et XIXe siècle Joseph Fourier. Les séries de Fourier possèdent une très grande variété d'applications dans beaucoup de domaines scientifiques, en particulier dans tous les phénomènes impliquant des périodicités saisonnières mentionnées ci-dessus, dans les mouvements ondulatoires, et par conséquent dans l'étude des radiations, en acoustique, en sismologie, dans la modulation des ondes radios en électronique, et dans la technologie de l'énergie électrique.

Une série de Fourier est une somme de la forme:

\begin{matrix} \square+\underbrace{\square\cos\theta+\square\sin\theta}_{1}+ \underbrace{\square\cos(2\theta)+\square\sin(2\theta)}_{2}+ \\ \\ \underbrace{\square\cos(3\theta)+\square\sin(3\theta)}_{3}+\,\cdots \\ \end{matrix}

où chacun des carrés ( $\square$ ) représente un certain nombre appelé coefficient, et les trois petits points signifient que des termes sont ajoutés une infinité de fois. Fourier employa ces séries pour étudier les flux de chaleur l'écoulement et la diffusion de la matière (la diffusion est le processus par lequel, lorsque vous laissez tomber un morceau de sucre dans un verre d'eau, le sucre se répartit graduellement par l'eau, (ou lorsqu'un polluant se propage dans l'air, ou n'importe quelle substance dissoute se répand dans n'importe quel fluide).

Les séries de Fourier s'appliquent également à des sujets d'étude dont le lien avec les mouvements ondulatoires est loin d'être évident. Un exemple omniprésent est la compression numérique par laquelle des données images, les audios et vidéos sont compressées dans une taille beaucoup plus petite rendant possible leur transmission via le téléphone, l'internet, les émissions sur les ondes et les réseaux informatiques.

Un autre exemple, mentionné ci-dessus, est la diffusion de la matière.

Parmi tant d'autres, il y a aussi: la géométrie des nombres, les problèmes isopérimétriques, les répétitions dans une promenade aléatoire, la réciprocité quadratique, le théorème de la limite centrale, l'inégalité d'Heisenberg.