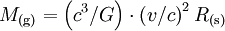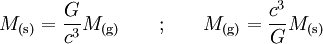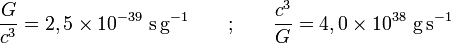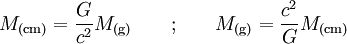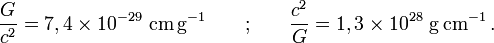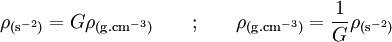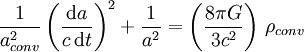Univers fini de Friedmann - Définition
La liste des auteurs de cet article est disponible ici.
Question d'unités
Le fait d'utiliser un système d'unités dans lequel la vitesse de la lumière c et la constante de la gravitation G valent l'unité (autrement dit disparaissent des formules) conduit à des formules plus simples à manipuler d'un point de vue mathématique, ainsi que le montrent les équations écrites ci-dessus. En conformité avec le choix de Wheeler, nous pourrions désigner ces unités sous le nom d'unités « géométrisées ». Mais cette façon de faire peut déconcerter plus d'une personne, surtout celles qui auraient la louable habitude de mener leurs calculs en étant attentives à l'homogénéité des formules et à la signification physique des termes manipulés. Voici donc quelques pistes pour jongler avec les systèmes d'unités employés en cosmologie.
Avant de continuer, précisons que nous emploierons comme unités « ordinaires », conventionnelles celles du système CGS : la seconde, le centimètre et le gramme. Ce choix est le fruit d'une longue habitude en astronomie et ne présente aucun inconvénient dans la mesure où ces unités dérivent immédiatement par une simple puissance de dix des unités du système international.
Il est également courant, en cosmologie, d'établir des équivalences entre des quantités physiques apparemment différentes, mais liées — en particulier, mais pas uniquement, par la lumière. Dans ce système d'unité, les facteurs disparaîssent, et on peut écrire des égalités directes, par exemple entre un temps et une distance. On propose ici quelques conversions élémentaires, en indiquant les unités en indice et en parenthèses.
Distances et durées
Soit une distance r, mesurée en centimètres. La conversion en unités de temps (secondes) se fait par la relation :
avec c la vitesse de la lumière en unités CGS, c'est-à-dire environ 3.1010 cm.s-1. Il s'agit alors du temps qu'il a fallu à la lumière pour parcourir cette distance. La conversion est réversible :
Ainsi la distance de la Terre au Soleil est-elle environ 150 millions de kilomètres, soit :
- 1,5×1013cm ;
- 500 s = 8,33 minutes de lumière.
De même, la distance qui nous sépare de la galaxie d'Andromède est d'environ 3 millions d'années-lumière, une année valant 3×107 secondes.
Masses, durées et distances
En ce qui concerne les unités de masse, nous devons naturellement introduire la constante de la gravitation universelle :
Prenons par exemple la formule donnant la vitesse v d'un mobile en orbite circulaire de rayon R autour d'une masse M, à savoir :
La masse est de même dimension que le rapport Rv²/G, ce qui permet de tracer un lien entre l'unité de masse et celle des autres grandeurs :
En utilisant les relations pour les distances, on a :
formule qui montre qu'on passe d'une masse en secondes à une masse en grammes en multipliant par la quantité
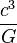
avec
La masse M peut encore s'exprimer en unités de distance, c'est-à-dire en centimètres, les formules de transformation étant :
avec
Le Soleil a une masse de 2×1033 grammes, soit :
- 5×10-6 seconde ;
- 1,5×105 centimètres (soit 1,5 kilomètres).
En unités « géométrisées » une masse par unité de volume, ou « densité » (comme la désignent incorrectement les astrophysiciens) est le rapport d'une masse (en secondes) à un volume (en secondes au cube) et s'exprime donc en (secondes)-2. Les formules ci-dessus conduisent facilement aux règles de conversion suivantes:
Conséquences
Ainsi l'équation d'Einstein d'un univers de Friedmann s'écrit-elle en unités conventionnelles sous la forme :
où aconv s'exprime en centimètres et ρconv en g / cm3.
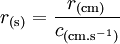
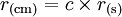
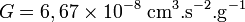
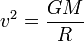
![M_{\rm (g)} = R_{\rm (cm)} \cdot \left[ v_{\rm (cm.s^{-1})} \right]^2 / G_{\rm (cm^3.s^{-2}.g^{-1})}](https://static.techno-science.net/illustration/Definitions/autres/c/cb420f8a3c6ec28bc19b9d5878169e9c_bb54a17470275d590bb86395509d32a6.png)