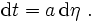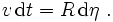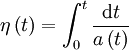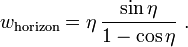Univers fini de Friedmann - Définition

Distance de l'horizon cosmologique

Quelle est l'interprétation physique de l'angle η ? En dérivant l' donnant le temps t en fonction du paramètre η on obtient la relation très simple

Cette forme est celle de l'expression ds = a(t) dχ écrite plus haut liant la longueur infinitésimale ds à la variation dχ de la coordonnée angulaire radiale χ le long d'une ligne de visée.

Puisque nous mesurons les distances en temps de lumière, la quantité de gauche dt représente la distance parcourue par un photon pendant le temps dt. Le terme de droite correspond à cette même distance exprimée maintenant à l'aide de la différentielle dη de la coordonnée angulaire η sur une hypersphère de rayon a. Comme plus haut, raisonnons par analogie avec le cas d'une surface sphérique à deux dimensions dans notre espace ordinaire à trois dimensions. Un mobile partant du pôle nord le long d'un grand cercle à la vitesse v parcourt la distance vdt pendant le temps dt. Sur une terre de rayon R l'arc représentant le trajet effectué peut aussi s'exprimer par Rdη, où dη est le déplacement en latitude η. On a donc :

La formule est exactement la même dans notre espace courbe à trois dimensions, considéré comme l'hypersurface d'un hypervolume sphérique à quatre dimensions (il suffit de remplacer v par 1 et R par a). Le paramètre η représente la coordonnée radiale angulaire d'un photon issu de l'origine. On peut désigner ce paramètre η sous le nom de « distance paramétrique angulaire ». C'est l'équivalent (pour un photon) du paramètre angulaire radial χ introduit dans la section sur la métrique. En effet, en reprenant l'expression de cette métrique FLRW le long du trajet radial d'un photon (dφ = dθ =0) et en écrivant que l'intervalle ds est nul, comme il se doit pour tout photon honnête, on obtient bien dt = a dχ.

Si a était constant et égal à R, on aurait tout simplement sur un intervalle de temps fini t = Rη ou η = t / R. Lorsque a est fonction de t, on a soit t en fonction de η donné par la formule paramétrique ci-dessus, soit η en fonction de t par l'intégrale

Le paramètre η a une interprétation physique encore plus fondamentale. Un photon issu de l'origine (le point où nous nous trouvons, disons le pôle nord) parcourt l'arc dη dans le temps dt et par conséquent l'arc total η(t) au bout du temps t. Réciproquement nous ne voyons autour de nous au temps t que les photons qui ont voyagé pendant un temps inférieur à t et qui sont issus de points dont la distance paramétrique angulaire est inférieure à η(t). Puisque par définition l'horizon cosmologique est la limite entre la partie observable de l'univers et sa partie inaccessible, nous pouvons énoncer :

C'est lorsque le paramètre η vaut π que l'univers est entièrement exploré, l'horizon cosmologique ayant atteint le point le plus éloigné, appelé anticentre (le pôle sud en quelque sorte si l'origine est vue comme le pôle nord). C'est aussi, nous l'avons noté, l'instant où l'univers atteint sa taille maximale, avec un rayon a=A, au temps π A / 2.

La « distance » de l'horizon cosmologique en un point lorsque l'univers a l'âge t peut s'exprimer sous différentes formes, selon la définition utilisée et le contexte. La plus simple est évidemment de dire que les photons issus de l'horizon ont voyagé pendant un temps t. Ils ont donc parcouru la « vraie distance » t. La distance en coordonnée comobile angulaire est η(t), que nous avons définie précédemment : elle est très commode à manipuler. Enfin, si on imaginait que l'expansion s'arrête brutalement au temps t, la distance « instantanée » de l'horizon cosmologique serait a(t) η (t) mais cette quantité n'a pas grande valeur physique pratique.

Des donnant la loi de Hubble, on peut trouver l'expression de la pseudo-vitesse de récession w_horizon à la distance de l'horizon cosmologique. Nous venons de dire en effet que cet horizon est situé à la distance paramétrique angulaire χ = η, de sorte que l'on obtient sans peine

Il est intéressant de remarquer que cette pseudo-vitesse peut devenir supérieure à la vitesse de la lumière. Par exemple pour η = 1 on trouve que w_horizon vaut 1,8 — c'est-à-dire 1,8 c en unités conventionnelles. Ce résultat nous montre que l'horizon cosmologique dans un univers de Friedmann n'est pas l'endroit où la vitesse de récession devient égale à la vitesse de la lumière, comme il est indiqué parfois à tort dans des ouvrages de vulgarisation.