Univers fini de Friedmann - Définition
La liste des auteurs de cet article est disponible ici.
La métrique FLRW
Pour rendre justice aux cosmologistes qui ont contribué après Friedmann à développer le modèle homogène fini satisfaisant aux équations de la théorie de la gravitation d'Einstein, on nomme métrique de Friedmann-Lemaître-Robertson-Walker celle qui permet de décrire la géométrie de l'espace-temps de l'univers homogène et isotrope de Friedmann. Dans la théorie d'Einstein, cette géométrie est entièrement décrite par ce que l'on appelle la métrique de l'espace-temps.
Par définition, la métrique donne la « distance », entendue au sens de la relativité restreinte, entre deux événements infiniment voisins. Si on repère un événement par ses quatre coordonnées spatio-temporelles (t, x, y, z), alors la distance relativiste entre deux événements dont les coordonnées diffèrent de dt, dx, dy, dz est donnée par :
en choisissant d'exprimer les distances en unités de temps, c'est-à-dire en secondes, ce que l'on fait couramment en astronomie. La formule permettant de passer des centimètres aux secondes est s (en secondes) = s (en centimètres)/c, où c est la vitesse de la lumière, soit 3×1010 cm/s.
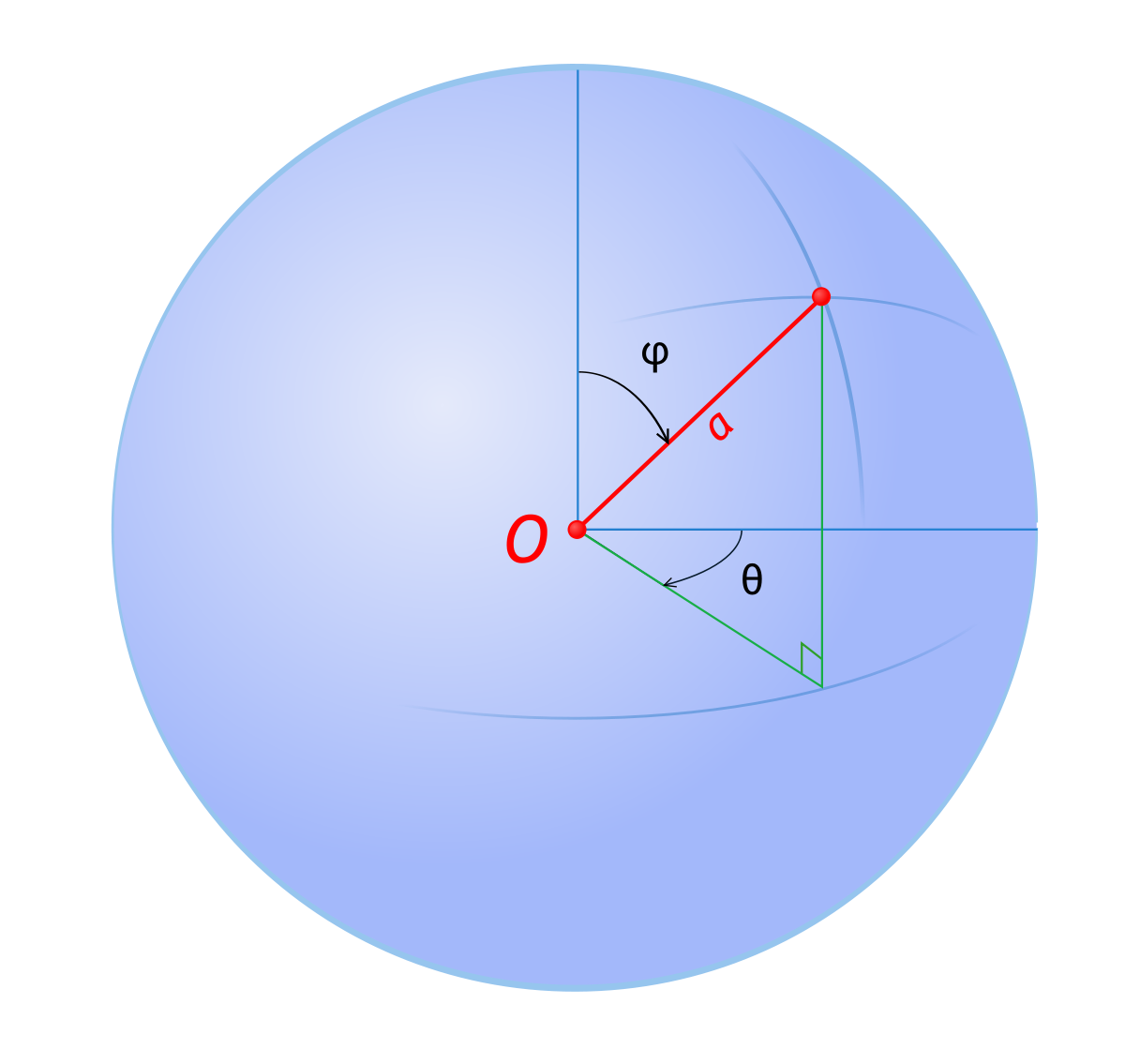
Il est facile d'écrire la métrique d'un univers courbe homogène à trois dimensions en généralisant le calcul de la distance entre deux points voisins d'une surface courbe à deux dimensions. En se plaçant en coordonnées cartésiennes (x, y, z), la surface à deux dimensions d'une sphère à trois dimensions de rayon a est décrite par l'équation :
On peut représenter cette surface sphérique à deux dimensions, en coordonnées polaires, à l'aide des deux paramètres angulaires, appelés latitude et longitude, notés respectivement θ et φ, sous la forme classique :
On a par ailleurs la métrique euclidienne spatiale :
On peut réécrire cette métrique en utilisant la paramétrisation donnée ci-dessus :
De façon similaire, notre propre espace (courbe, homogène, à trois dimensions) peut être considéré comme l'hypersurface à trois dimensions d'une boule à quatre dimensions et de rayon a. Une telle boule est l'ensemble des points solutions dont les coordonnées sont liées par l'équation :
On peut donc représenter notre espace à trois dimensions, en coordonnées polaires, à l'aide de trois paramètres angulaires θ, φ et χ sous la forme :
On en déduit la métrique spatiale :
Les paramètres angulaires θ et φ servent à fixer la direction du point considéré tandis que l'angle χ fixe sa distance radiale. Le long d'une ligne de visée donnée (dφ = dθ=0), on voit que la distance radiale élémentaire entre deux points est de la forme ds = a(t) dχ, la même que celle donnant sur un cercle ordinaire de rayon R la longueur ds de l'arc d'angle au centre dχ, à savoir ds = R dχ.
La métrique relativiste de l'espace-temps homogène et isotrope FLRW s'écrit finalement :
où a est une longueur à laquelle on peut donner le nom de « rayon de l'univers ». Toutefois il faut prendre conscience du fait que ce rayon est celui d'une sphère à quatre dimensions et qu'on ne peut donc pas le visualiser. En revanche le paramètre a est une vraie longueur, qui s'exprime donc en secondes (ou plutôt en dizaines de milliards d'années pour notre Univers). La signification physique de cette longueur a est de donner l'échelle de distance à partir de laquelle la courbure se manifeste. En effet de même qu'un petit jardin à la surface de la Terre est comme plat (on pourrait désigner cette proposition comme le théorème du jardin), de même une portion d'espace très petite devant le rayon a ne manifestera pas de courbure.
Cette forme de la métrique suppose que l'on a accepté avec Einstein la condition de fermeture de l'Univers (l'univers fini est aussi appelé univers fermé), en refusant comme physiquement inconséquente la solution d'un univers infini (dit aussi ouvert). Incidemment, dans le cas infini les fonctions trigonométriques sont remplacées par des fonctions hyperboliques, la métrique prenant alors la forme :
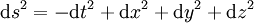
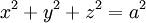
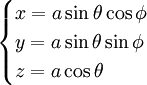
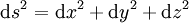
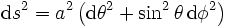
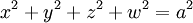

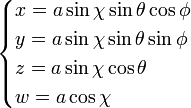
![\mathrm ds^2 = a^2 \left( t \right) \left[ \mathrm d\chi^2 + \sin^2\chi \left( \mathrm d\theta^2 + \sin^2\theta \,\mathrm d\phi^2 \right) \right]~](https://static.techno-science.net/illustration/Definitions/autres/9/9fd531031390704cc080cbe320bdba96_4f6da9bdd2329afbb3d59b18d006562b.png)
![\mathrm ds^2 = - \mathrm dt^2 + a^2 \left(t \right) \left[ \mathrm d\chi^2 + \sin^2\chi \left( \mathrm d\theta^2 + \sin^2\theta \,\mathrm d\phi^2 \right)\right]~](https://static.techno-science.net/illustration/Definitions/autres/f/f2bcdf612253cdca6b82ae20b71387b7_dbc45d0b87909b5b70630675bea943fe.png)
![\mathrm ds^2 = - \mathrm dt^2 + a^2 \left(t \right) \left[ \mathrm d\chi^2 + \sinh^2\chi \left( \mathrm d\theta^2 + \sinh^2\theta \mathrm d\phi^2 \right) \right].](https://static.techno-science.net/illustration/Definitions/autres/d/de1de77cea86a78ffe05f8596b99a005_6c374a449ab2ad82456f14d65589ad68.png)

















































