Valeur propre (synthèse) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les notions de vecteur propre, de valeur propre, et d'espace propre s'appliquent à des endomorphismes (ou opérateurs linéaires), c'est-à-dire des applications linéaires d'un espace vectoriel dans lui-même. Elles sont intimement liées, et forment un pilier de la réduction des endomorphismes, partie de l'algèbre linéaire qui vise à décomposer de la manière la plus efficace possible l'espace en somme directe de sous-espaces stables.
Cet article résume les propriétés mathématiques essentielles associées à ces notions et renvoie vers des articles dédiés pour un approfondissement.
L'article Valeur propre, vecteur propre et espace propre détaille l'historique de ces concepts ainsi que leurs utilisations aussi bien dans le champ des mathématiques que dans les autres branches scientifiques.
Définitions et propriétés
Dans toute la suite, on considère un espace vectoriel E sur un corps commutatif
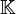
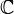
Valeur propre
Définition formelle:
Soit
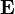
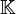
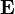
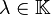
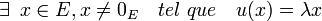
L'ensemble des valeurs propres de u est appelé spectre de u noté Sp(u).
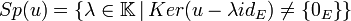
C'est donc l'ensemble des scalaires λ tels que l'application u − λidE ne soit pas injective (autrement dit son noyau n'est pas restreint au vecteur nul).
Si E est de dimension n, alors u possède au plus n valeurs propres.
Exemples :
- si u = Id alors u ne possède qu'une valeur propre : 1.
- si u est définie sur
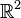
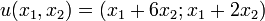
- 4 car u(2 ; 1) = (8 ; 4) = 4(2 ; 1)
- -1 car u(-3 ; 1) = (3; -1) = -1 (-3 ; 1)
- pas d'autre valeur propre puisque la dimension est 2.
On parle aussi de valeur propre d'une matrice carrée. En effet, une matrice carrée est la représentation d'un endomorphisme sur
Vecteur propre
Soit x un vecteur non nul de E, x est un vecteur propre de l'endomorphisme u si et seulement s'il existe un scalaire λ tel que u(x) = λx . On dira que x est un vecteur propre associé à la valeur propre λ.
- Un vecteur propre ne peut pas être associé à deux valeurs propres différentes
- Une famille de k vecteurs propres associés à k valeurs propres différentes constitue une famille libre.
Dans le cas d'une valeur propre associée à une matrice carrée, on emploie souvent le terme de colonne propre plutôt que celui de vecteur propre.
Sous-espaces propres
Soit λ une valeur propre de u ; alors l'ensemble constitué des vecteurs propres de valeur propre λ, et du vecteur nul, forme un sous-espace vectoriel de E appelé sous-espace propre de u associé à la valeur propre λ.
- Soit λ une valeur propre, alors l'espace propre de valeur propre λ est le sous-espace vectoriel égal au noyau de u - λ.Id.
- Par définition d'une valeur propre, un espace propre n'est jamais réduit au vecteur nul.
- Les espaces propres Ei de valeurs propres λi forment une somme directe de sous-espaces vectoriels stables par u.
- Cette propriété se démontre simplement avec les outils développés dans l'article Polynôme d'endomorphisme. X - λi est un polynôme annulateur de la restriction de u à Ei. Ces polynômes sont tous premiers entre eux, la dernière proposition du paragraphe Idéaux annulateurs termine la démonstration.
- La somme directe ne fait pas pour autant des Ei des sous-espaces supplémentaires. Ce ne sera le cas que lorsque l'endomorphisme sera diagonalisable.
- Si deux endomorphismes u et v commutent, alors tout espace propre de u est stable par v.
- Soit x un vecteur propre de u, de valeur propre λ ; alors:
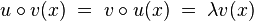
- Nous avons donc démontré que v(x) est soit nul soit vecteur propre de valeur propre λ: il est donc bien élément de l'espace propre de λ.
Polynôme caractéristique
On se place ici dans le cadre d'un espace vectoriel E de dimension finie n.
On appelle polynôme caractéristique de l'endomorphisme u, le polynôme formel det(u − X.Id)
- Les racines du polynôme caractéristique sont les valeurs propres de u.
- Une des propriétés du déterminant est d'être nul si et seulement si le noyau de l'endomorphisme associé est non réduit au vecteur nul. Cela signifie que λ est racine du polynôme caractéristique si et seulement si le noyau de u - λ.Id est non réduit au vecteur nul, ce qui est une condition nécessaire et suffisante pour que λ soit une valeur propre.
- Soit a un automorphisme, c'est-à-dire un endomorphisme bijectif, alors si u est un endomorphisme, u et a-1.u.a ont même polynôme caractéristique et donc mêmes valeurs propres.
- En effet, l'article sur les déterminants nous montre que:
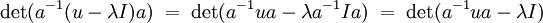
- Si
- Dire qu'un corps est algébriquement clos, c'est dire que tout polynôme de degré différent de zéro admet au moins une racine. Cette racine est nécessairement une valeur propre, d'après la première propriété de ce paragraphe. De plus, les polynômes réels ont toujours une racine si le degré est impair. Cela termine la démonstration.
L' ordre de multiplicité algébrique d'une valeur propre est l'ordre de multiplicité de la racine dans le polynôme caractéristique. L'ordre de multiplicité algébrique d'une valeur propre λ correspond donc à la puissance du monôme (X-λ) dans le polynôme caractéristique.
- Dans un corps algébriquement clos,
- Le déterminant est égal au produit des valeurs propres élevées à leur ordre de multiplicité algébrique.
- La trace est égale à la somme des valeurs propres multipliées par leur ordre de multiplicité algébrique.
Polynôme minimal
On se place ici en dimension finie. Le polynome minimal est le polynôme normalisé (son facteur de plus haut degré est égal à 1) de plus petit degré qui annule l'endomorphisme u
- Le théorème de Cayley-Hamilton permet d'affirmer que le polynôme minimal divise le polynôme caractéristique
- Les racines du polynôme minimal forment l'ensemble des valeurs propres de u
Sous-espaces caractéristiques
On se place dans un espace vectoriel E de dimension finie n sur un corps
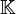
Si λi est une valeur propre de u, dont l'ordre de multiplicité est αi, on appelle sous-espace caractéristique de u associé à la valeur propre λi le noyau de
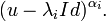
- Ei est aussi le noyau de
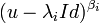
- Ei est stable par u
- dim(Ei) = αi
- L'espace E est somme directe de ses sous-espaces caractéristiques
- la restriction de u à Ei a pour polynôme minimal