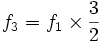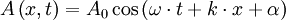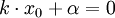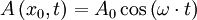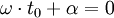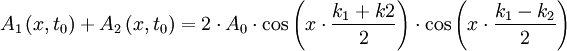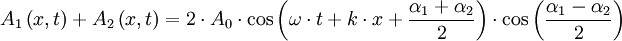Battement - Définition

En physique, la superposition de deux ondes de fréquence, de nombre d'onde ou de phase différentes donne lieu au phénomène de battement. On l'observe de fait dans tous les domaines ou interviennent des ondes, notamment l'acoustique et l'optique.

Acoustique musicale

En acoustique musicale, le battement est une perception sonore due au mélange de deux sons, de fréquences fondamentales voisines, ou contenant des fréquences harmoniques voisines. C'est l'équivalent sonore des franges de moiré que l'on peut observer en optique.

Lorsque deux sons sont de fréquences ƒ₁ et ƒ₂ très proches — donc de hauteurs voisines — l'oreille perçoit une sorte de pulsation lente dont la fréquence est la différence ƒ₁ - ƒ₂ en valeur absolue.

Par exemple, un la à 440 Hz joué en même temps qu'un la à 443 Hz produiront conjointement une pulsation de 1,5 battements par seconde :

•  ^{Battements 440 Hz et 440,5 Hz}
•  ^{Battements 440 Hz et 442 Hz}

Un battement est également perçu entre des sons de fréquence ƒ₂ et ƒ₃ si cette dernière est une fréquence harmonique simple de ƒ₁. Par exemple, si ƒ₃ est la quinte de ƒ₁, alors :

Les battements se produisent en fait en grand nombre entre toutes les fréquences en présence, mais la plupart ne sont pas audibles. En effet, il est possible que ces battements ou les sons résultants correspondent à des fréquences existantes, qui sont alors renforcées, ou bien qu'elles soient de trop faible intensité ou qu'elles varient trop lentement (un battement toutes les 5 secondes ou plus lent). On ne les entendra pas non plus si les battements sont trop rapides : au-delà de 20 battements par secondes, ils ne sont plus discernables, et on entre dans le champ des fréquences audibles : 20 Hz (extrême grave) étant considéré comme le seuil auditif d'une oreille ordinaire. Le phénomène reste le même, mais on parle alors, à cause du changement de perception, de son résultant.

Le phénomène de battement s'entend très bien lorsqu'une personne accorde un instrument à corde (par exemple une guitare) : on entend une vibration du son, due au mélange des sons émis par les deux cordes pincées ensemble. C'est ce phénomène qui permet d'effectuer, simplement à l'oreille, l'accord des instruments de musique : un intervalle est pur lorsqu'on n'entend plus aucun battement.

Mais inversement, l'existence d'un battement reconnu permet également d'effectuer l'accord ou l'intonation. Par exemple, la tierce majeure n'est jamais utilisée pure (sauf en musique ancienne), la qualité de son battement permet aux instrumentistes de s'assurer qu'ils jouent juste.

Des méthodes d'accordage emploient aussi comme outil infaillible, mais pas toujours pratique, le comptage des battements : leur vitesse indique avec une grande précision l'état des l'intervalles tempérés indispensables à l'accord d'un instrument à sons fixes.

Des intervalles moins consonants, bien que " justes ", tels que les seconde ou sixte mineures, peuvent également générer des battements qui sont constitutifs de leur nature. C'est là la raison de leur faible consonance. Même des intervalles assez consonants en contiennent : voir le cas intéressant de la tierce.

Cas général

Les ondes peuvent être représentées par des fonctions trigonométriques : en effet, le théorème de Fourier garantit que l'on peut décomposer toute fonction périodique comme somme de fonctions trigonométriques.

Supposons des ondes linéaires, solutions de l'équation de d'Alembert, se propageant transversalement sur une dimension : par exemple une corde vibrante. Alors le déplacement en un point d'abscisse x, à un instant t par rapport à la position de repos est donné par la formule :

avec ω la pulsation (en rad·s^-1), k le nombre d'onde (en rad·m^-1), α la phase à l'origine (en rad) et A₀ l'amplitude de l'onde.

On peut relier la pulsation à la fréquence par cette équation :

ω = 2πf

Battements dans le temps

Battements interférentiels de deux ondes de fréquence proches (10 % de différence).

Pour simplifier, on se place en un point fixe, d'abscisse x₀, et on étudie les battements qui se produisent en ce point, dans le temps.

On choisit x₀ de sorte que :

On a alors, à tout instant t :

Puisque l'on a des interférences entre deux ondes, il faut sommer deux fonctions trigonométriques. Cela peut être fait en utilisant les formules d'addition :

.

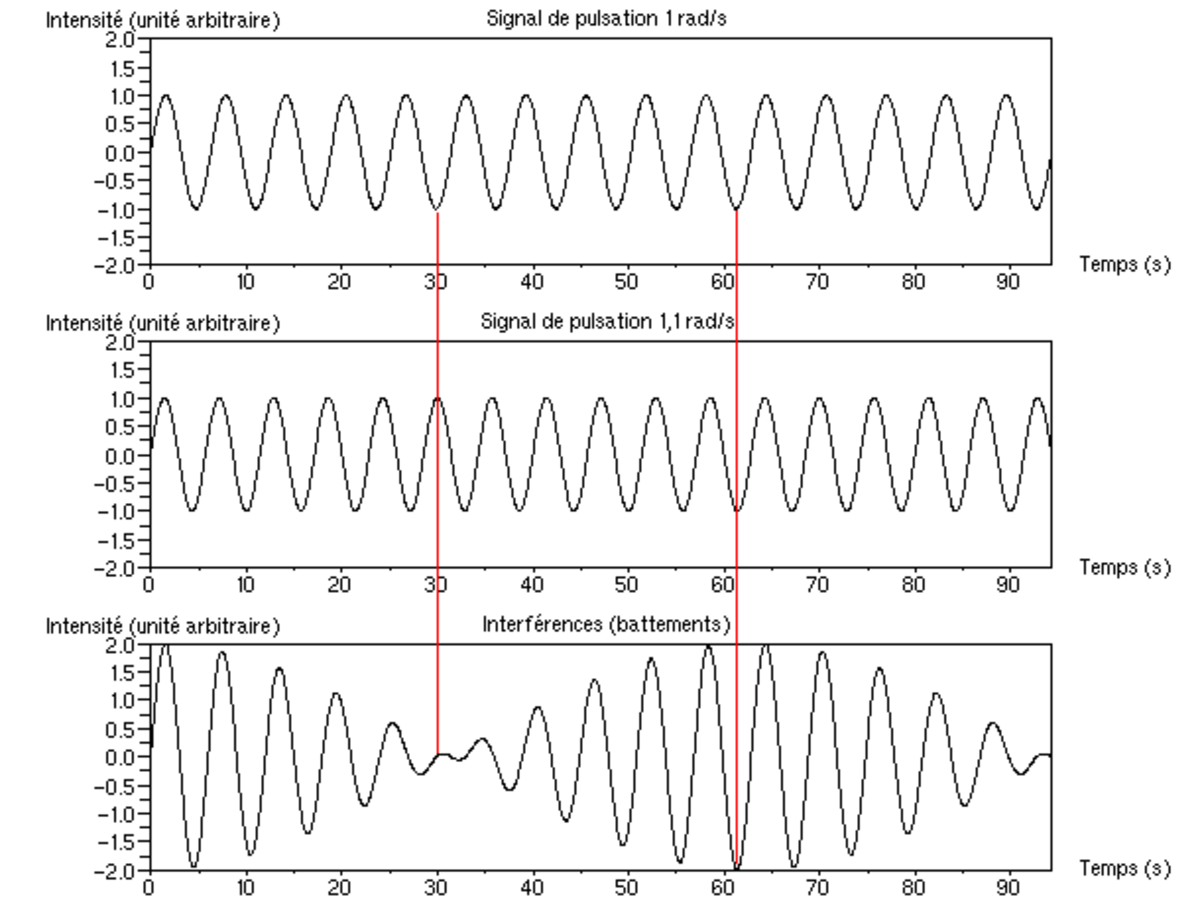
Supposons que se propagent deux ondes de même amplitude, mais de pulsations différentes. Alors le déplacement en un point et la somme des contributions des deux ondes :

Il apparaît que l'onde totale peut être décomposée en une onde " de base ", de pulsation rapide (ω₁ + ω₂) / 2^[1], et en une onde de pulsation lente (ω₁ − ω₂) / 2 qui fait varier l'amplitude de la première.

Battements dans l'espace

Battements d'interférence selon l'endroit à un instant donné, pour une différence de nombre d'onde de 10 %.

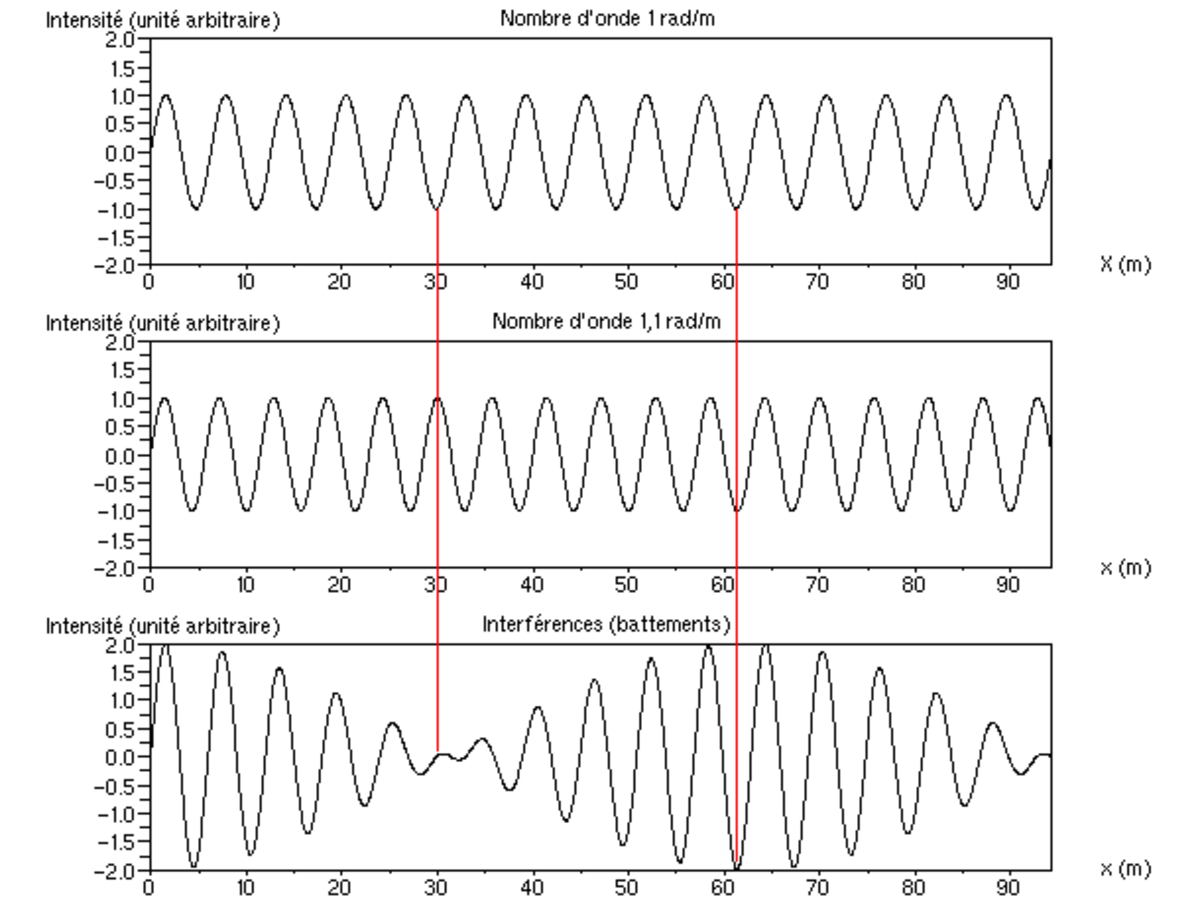
Il est possible de réaliser l'étude complémentaire : on fixe un instant t₀ et on regarde l'onde dans l'espace.

On choisit t₀ de sorte que :

De même que précédemment, l'onde totale est la somme des deux ondes de nombres d'onde différents :

on obtient une figure spatiale d'interférence, ayant également une variation de petite longueur d'onde (k ₁ + k ₂)/2 et une variation de grande longueur d'onde (k ₁ - k ₂)/2^[2]

Différence de phase

Si l'on considère maintenant des ondes de même amplitude A, de même pulsation ω (donc de même nombre d'onde k) mais de phase α différente, on a :

L'onde résultante a donc la même pulsation, mais sa phase à l'origine et son amplitude dépendent des phases des ondes interférentes.

Si α₁ = α₂ [2π], le facteur cos((α₁ - α₂)/2) vaut cos(0) = 1, on a donc une onde d'amplitude double ; on parle d'interférences constructives et on dit que les ondes sont " en phase ".

Si en revanche α₁ = α₂ + π [2π], le facteur cos((α₁ - α₂)/2) vaut cos(π/2) = 0, les ondes s'annulent ; on parle d'interférences destructives et on dit que les ondes sont " en opposition de phase ".

Entre ces situations, l'amplitude passe de 2·A₀ à 0 en fonction du facteur cos((α₁ - α₂)/2). Les endroits où l'on a une extinction du son pour deux haut-parleurs branchés en opposition de phase correspondent aux lieux pour lesquels les ondes sont toujours en opposition de phase.

Notes et références