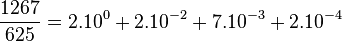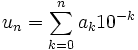Développement décimal - Définition
En mathématiques, le développement décimal est une façon d'écrire des nombres réels positifs à l'aide des puissances de 10 (négatives ou positives). Lorsque les nombres sont des entiers naturels, le développement décimal correspond à l'écriture en base 10. Lorsqu'ils sont décimaux, on obtient un développement décimal limité. Lorsqu'ils sont rationnels, on obtient un développement décimal illimité périodique. Enfin, lorsqu'ils sont irrationnels, le développement décimal est illimité et non périodique.
Cas des nombres entiers
Tout nombre entier possède une écriture décimale qui nous est naturelle car enseignée depuis notre enfance. Nous prenons conscience du fait qu'il ne s'agit que d'une écriture lorsque les circonstances nous mettent en contact avec d'autres systèmes de numération.
Exemple : 123 827 = 1×105 + 2×104 + 3×103 + 8×102 + 2×101 + 7×100
Cas des nombres décimaux
Un nombre décimal est un nombre pouvant s'écrire sous la forme
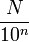
Un nombre décimal positif possède alors un développement décimal limité comportant des puissances de 10 à exposant négatif mais le plus petit exposant ne peut être que - n.
Exemple :
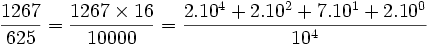
Et on vérifie très simplement à l'aide d'une calculatrice que
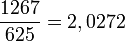
Réciproquement : tout nombre possédant un développement décimal limité est un nombre décimal car il suffit de le multiplier par la puissance de 10 adéquate pour retomber sur un entier.
Cas des nombres rationnels
Aborder l'écriture décimale de certains nombres rationnels nous fait rentrer dans le monde de l'infini car l'écriture ne s'arrête jamais. On parle de développement décimal illimité.
exemple: Division de 13 par 7
13 |7 60 |1,85714285... 40 | 50 | 10 | 30 | 20 | 60 | 40 | |
Puisque l'on obtient de nouveau le reste 6 (avant dernière ligne), en abaissant le 0, on se trouvera à diviser encore 60 par 7 à réobtenir pour quotient 8, pour reste 4 etc. Le cycle 857142 s'appelle la période du développement décimale illimité périodique. On écrira
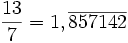
La période du développement décimal ne commence pas toujours juste après la virgule :
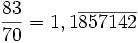
On peut démontrer que tout nombre rationnel possède un développement décimal illimité périodique. Pour le comprendre, il suffit de généraliser le principe de la division précédente. Supposons que l'on divise P par Q, dans la division de P par Q, on est amené, pour les décimales après la virgule, à " abaisser des zéros ". Si le reste précédent est r, on cherche alors à diviser 10r par Q. Les restes de la division sont en nombre fini (0, 1, ..., Q - 1), donc on ne peut pas prolonger indéfiniment la division sans rencontrer deux restes identiques. Si on appelle r1 et r'1 les deux premiers restes identiques, on voit que la division de 10r1 par Q sera identique à celle de 10r2 par Q, donnera le même quotient q1 = q'1 et même reste r2 = r'2 et ainsi de suite.
Un nombre décimal possède aussi un développement décimal illimité de période 0.
Réciproquement, tout développement décimal illimité périodique correspond à l'écriture d'un rationnel.
- Exemple : 3,25723723723... = x
- 100x = 325,723723723...
- 100x - 325 = y = 0,723723723... On peut remarquer que, si y est rationnel, x le sera aussi.
- y = 0,723723....
- 1000y = 723,723723723...
- 1000y = 723 + y
- 999y = 723
-
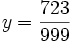
La méthode se généralise pour tout développement décimal illimité périodique. On se débarrasse de la mantisse par une multiplication par la puissance de 10 adéquate et par la soustraction d'un nombre entier. On obtient alors un nombre y s'écrivant 0,périodepériodepériode.... sur lequel on effectue le même type d'opération que plus haut : multiplication par la puissance de 10 adéquate 10ny = période + y . La résolution de l'équation précédente prouve que y est rationnel et donc que x est rationnel.
Cette méthode de décalage sera employée par la suite pour calculer de façon analogue la somme des termes d'une suite géométrique.
Cas particulier de 0,99999999... = y.
En utilisant la technique précédente, on obtient 10y = 9,99999... = 9 + y. La résolution de l'équation précédente mène donc à y = 1.
1 possède donc deux " développements décimaux illimités " périodiques : 1,000000... et 0,9999.... Selon la définition d'un développement décimal illimité sur

Cas des nombres réels
Si x est un nombre réel, on construit les suites de nombres décimaux suivantes :
-
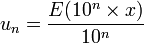
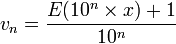
un s'appelle l'approximation décimale de x par défaut à 10-n et vn celle par excès.
On démontre facilement que un et un+1 ne diffèrent (éventuellement) que sur la n+1e décimale qui est de 0 pour un et de an+1 pour un+1.
un s'écrit alors
où tous les ak pour k = 1 à n sont des entiers compris dans {0, ..., 9}
On démontre aussi que (un) et (vn) sont des suites adjacentes encadrant x donc elles convergent vers x. On appelle alors développement décimal illimité la suite (an) et on remarquera que
-
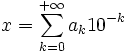
Réciproquement, si (an) est une suite d'entiers tels que tous les ak pour k = 1 à n sont des entiers compris dans {0, ..., 9}, on démontre que la série
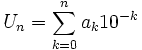
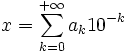
- Si la suite (an) converge vers 9 (tous les termes égaux à 9 à partir d'un certain rang k). Alors x est un décimal d'ordre k - 1. La suite (un) définie dans la première partie ne coincidera pas à la suite (Un). La suite (an) ne sera pas appelée un DDI.
- Si la suite ne converge pas vers 9, la suite (un) définie dans la première partie coincidera à la suite (Un) . La suite (an) sera appelée un DDI.
Cette construction d'un développement illimité permet de retrouver le développement d'un décimal 3,5670000.... , d'un rationnel 3,25743743743...... non impropre.
On démontre que cette définition construit une bijection entre les réels et les suites (an) d'entiers tels que tous les ak pour k = 1 à n sont des entiers compris dans {0, ..., 9} ne convergeant pas vers 9.
Régularité dans les développement décimaux illimités
Sauf pour les décimaux et les rationnels dont le développement illimité est périodique, il n'est en général pas possible de " prévoir " les décimales d'un réel. Seuls des calculs poussés permettent de découvrir les premières décimales (on connaît jusqu'à présent les 1 241 100 000 000 premières décimales de π.
Des études portant sur la fréquence des entiers dans les développement décimaux de

Lorsque les fréquences d'apparition de chaque chiffre est de 10% dans le développement décimal, on dit que le réel est un nombre normal.
Curiosités
- Le réel dont le développement décimal est 0,1234567891011121314151617... possède un développement décimal prévisible non périodique. Ce réel est la constante de Champernowne, du nom du mathématicien anglais qui l'a inventé en 1933. Ce nombre est évidemment irrationnel, mais aussi transcendant (prouvé par Kurt Mahler en 1961).
- La constante de Copeland-Erd?s 0,2357111317192329313741... constituée de la succession des nombres premiers.
- Le réel dont le développement décimal est 0,110001000000000000000001..., c'est-à-dire la somme des puissances factorielles négatives de 10 (10-1 + 10-2 + 10-6 + ...+ 10 -k! + ...) possède un développement décimal prévisible non périodique. Ce réel est la constante de Liouville, du nom du mathématicien français qui l'a inventé. Ce nombre est irrationnel, mais aussi transcendant (prouvé par Joseph Liouville).
- Le développement décimal est impossible dans un système positionnel sans zéro, c'est-à-dire que le développement décimal dépend non seulement d'un système de numération positionnel, mais également de l'usage du zéro positionnel.
Développement en base quelconque
Utiliser un développement décimal fait jouer un rôle particulier à la base 10. Tout ce qui précède s'applique à n'importe quel nombre entier b (comme base), supérieur à 1. Cette fois, les nombres admettant deux développements seront ceux de la forme
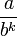
En fait la base 10 présente surtout un intérêt pratique, c'est celle à laquelle nous sommes habitués. Les bases 2 et 3 notamment sont très intéressantes. Plaçons nous en base 2. L'application de
![d:\{0,1\}^\N \rightarrow [0,1]](https://static.techno-science.net/illustration/Definitions/autres/d/d647a8a70831a9fe1efc9121f40efc6c_f5e073c01b149b6627a2679f711d7e39.png)
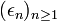
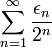
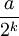
Plaçons nous maintenant en base 3. L'application qui aà la même suite
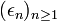
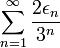
![[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d09694b77d8a3a03f6879fa37f09d0b0_c0411dcdc7776b6e09605dc7ec8741eb.png)
![[0,1]\times[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/7/709ba53bd4deaad714fb66ca0a272758_090d3ceb01660d1bfe72f925519ebc5e.png)