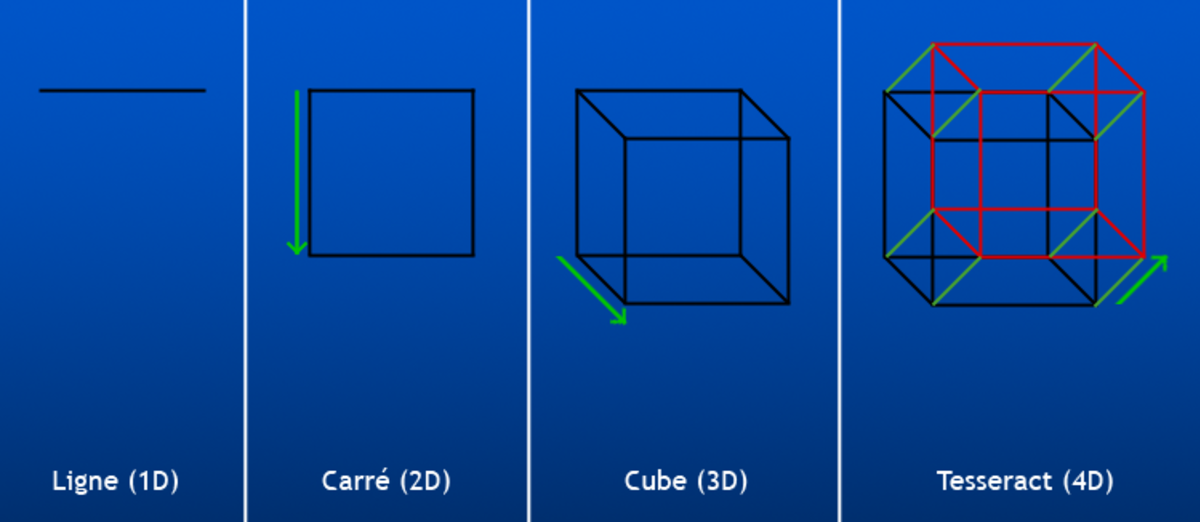
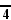Hypercube - Définition

Une projection d'un hypercube (dans une image bi-dimensionnelle)

En géométrie, un hypercube est un analogue n-dimensionnel d'un carré (n = 2) et d'un cube (n = 3). C'est une figure fermée, compacte, convexe constituée de groupes de segments parallèles opposés aligné dans chacune des dimensions de l'espace, en angle droit les uns les autres.

Un hypercube n-dimensionnel est aussi appelé un n-cube. Le terme "polytope de mesure" (qui est apparemment dû à Coxeter; voir Coxeter 1973) est aussi utilisé mais il est rare.

Définition

Si E est un espace euclidien de dimension n muni d'une base orthonormale, on peut définir un hypercube unité comme l'hypercube dont les 2ⁿ points dans Rⁿ avec des coordonnées égales à 0 ou 1. Les hypercubes sont les figures obtenues à partir de l'hypercube unité par des similitudes.

Représenter un hypercube de dimension n

Pour représenter un hypercube de dimension n, on procède comme suit :

• Dimension 1 : Un point est un hypercube de dimension zéro. Si on déplace ce point d'une longueur unité, il balaiera un segment de droite, qui est un hypercube unité de dimension un

• Dimension 2 : Si on déplace ce segment d'une longueur unité dans une direction perpendiculaire à partir de lui-même; il balaie un carré bi-dimensionnel.

• Dimension 3 : Si on déplace le carré d'une longueur unité dans la direction perpendiculaire à l'emplacement de celui-ci, il engendrera un cube tri-dimensionnel.

• Dimension 4 : Si on déplace le cube d'une longueur unité dans la quatrième dimension, il engendrera un hypercube unité quadri-dimensionnel (un tesseract unité).

...

• Dimension n > 3 : On trace un hypercube de dimension n-1, on reproduit son image et on lie les points deux à deux

En résumé, la construction d'un cube se fait par la translation du cube de dimension inférieure selon un axe perpendiculaire aux dimensions de ce cube.

Chaque nouvelle dimension est perpendiculaire aux précédentes

Les hypercubes sont une des quelques familles de polytopes réguliers qui sont représentés dans un nombre quelconque de dimensions. Le polytope dual d'un hypercube est appelé un polytope croisé. le 1-squelette d'un hypercube est un graphe hypercube.

Une généralisation du cube aux dimensions plus grandes que trois est appelée un “hypercube”, “n-cube” ou “polytope mesure”. Le tesseract est l'hypercube quadri-dimensionnel ou 4-cube. C'est un polytope régulier. C'est aussi un cas particulier de parallélotope : un hypercube est un parallélotope droit dont les arêtes sont de même longueur.

4 dimensions

L’hypercube à quatre dimensions est également appelé tesseract en anglais, d'après Charles Howard Hinton.

D'après la formule de Gardner, on peut retrouver les propriétés du tesseract en développant (2x + 1)⁴ :

Donc l'hypercube est composé de :

• 16 sommets ;
• 32 arêtes ;
• 8 faces cubiques (soit 24 faces planes) : chacune des faces du tesseract est un cube.

L'intersection d'un hypercube avec un hyperplan donne l'équation cartésienne :

Avec les quatre coordonnées de l'hyperespace de dimension 4, à savoir x, y, z, et w. En réalité, un hyperplan en quatre dimensions peut être comparé à l'espace tridimensionnel, c’est-à-dire que l'intersection d'un hypercube avec un plan est en fait une projection 3D de cet hypercube.

• Volume : c⁴, avec c le côté de l'hypercube.
• Aire totale : 24c²

Les faces d'un hypercube sont :

• Avant / Arrière
• Gauche / Droite
• Haut / Bas
• Ana / Kata

n dimensions

Un hypercube à n dimensions possède :

• V_n = 2ⁿ sommets ;
• S_n = 2 × S_n-1 + V_n-1 arêtes ; (ou n × 2^n-1)
• F_n = 2 × F_n-1 + S_n-1 faces planes ;
• HF_n = 2 × HF_n-1 + F_n-1 hyperfaces (cubes ou faces cubiques) ;
• Il en va de même pour les hyperfaces en 5 dimensions (faces hypercubiques) etc.
• De manière générale, le nombre de faces à k dimensions d'un hypercube à n dimension est égal à

• Le nombre total de faces d'un hypercube est de 3ⁿ − 1
• Volume = cⁿ avec c le côté de l'hypercube
• Aire totale = F_nc² avec F_n le nombre de faces

Éléments

Un hypercube de dimension n possède 2n "cotés" (un segment 1-dimensionnel a deux points aux extrémités; un carré 2-dimensionnel a quatre bords; un cube 3-dimensionnel a 6 faces 2-dimensionnelles; un hypercube 4-dimensionnel (tesseract) a 8 cellules). Le nombre de sommets (points) d'un hypercube est 2ⁿ (un cube a 2³ sommets, par exemple).

Le nombre d'hypercubes m-dimensionnels (comme désigné sous le nom m-cube ci-dessus) sur la frontière d'un n-cube est

Par exemple, la frontière d'un 4-cube contient 8 cubes, 24 carrés, 32 segments et 16 sommets.

Éléments d'hypercube

n-cube	Graphe	Noms Symbole de Schläfli Coxeter-Dynkin	Sommets (0-faces)	Arêtes (1-faces)	Faces (2-faces)	Cellules (3-faces)	(4-faces)	(5-faces)	(6-faces)	(7-faces)	(8-faces)
0-cube		Point -	1
1-cube		Digone {} ou {2}	2	1
2-cube		Carré Tétragone {4}	4	4	1
3-cube		Cube Hexaèdre {4,3}	8	12	6	1
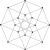
4-cube		Tesseract octachore {4,3,3}	16	32	24	8	1
5-cube		Penteract déca-5-tope {4,3,3,3}	32	80	80	40	10	1
6-cube		Hexeract dodéca-6-tope {4,3,3,3,3}	64	192	240	160	60	12	1
7-cube		Hepteract tétradéca-7-tope {4,3,3,3,3,3}	128	448	672	560	280	84	14	1
8-cube		Octeract hexadéca-8-tope {4,3,3,3,3,3,3}	256	1024	1792	1792	1120	448	112	16	1
9-cube		Ennéneract octadéca-9-tope {4,3,3,3,3,3,3,3}	512	2304	4608	5376	4032	2016	672	144	18

Rotation d'un n-cube

Rotation d'un hypercube.

Basé sur nos observations de la manière dont les objets 1, 2 et 3 dimensionnels peuvent tourner, nous pouvons émettre une hypothèse sur la manière dont tournent les objets à n dimensions. Un objet 3-dimensionnel peut tourner de deux manières différentes sur 3 axes. Par la première, il peut tourner sur une arête. Un cube (par exemple) peut tourner sur un arête entière, ce qui signifie que tout change de position sauf cette arête. Par la deuxième, il peut tourner sur un point unique. Il est possible de faire tourner un cube autour d'un point unique, sans que ce point ne change de position. De manière similaire, un objet 2-dimensionnel peut tourner sur un point unique, mais c'est la seule manière dont il peut tourner. Donc, un cube 3-dimensionnel peut tourner sur sa 1ère dimension ou la 0ème dimension, et un plan 2-dimensionnel peut seulement tourner sur la 0ème dimension. Ainsi, qu'en est-il de la première dimension ? Selon notre théorie, il pourrait tourner autour de la dimension -1, dimension négative qui est le néant ou la non-existence, ce qui a un sens, parcequ'il ne peut pas tourner. Ceci conforte notre hypothèse depuis la première jusqu'aux trois dimensions, donc, nous pouvons par conséquent supposer que cela s'appliquera pour toutes les autres dimensions. Ceci signifie qu'un hypercube 4-dimensionnel peut tourner autour d'une face entière, qu'un hypercube 5-dimensionnel peut tourner autour d'un cube entier, etc...

Les hypercubes en science-fiction

Cube, Cube²: Hypercube et Cube Zero sont des films de science-fiction dans lequel des personnes sont enfermées dans un labyrinthe de cubes temporels.