Drapeau (mathématiques) - Définition

Un drapeau de l'espace vectoriel de dimension finie E est une famille de sous espaces successifs de E, inclus les uns dans les autres, et dont les dimensions augmentent de 1 en 1.

Formellement, si est de dimension il s'agit d'une famille de n+1 sous-espaces vectoriels de telle que:

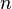
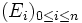
Exemple : si E est l'espace des polynômes de degré inférieur ou égal à n, les espaces successifs pour i allant de 0 à n constituent un drapeau de E.

Base adaptée à un drapeau

A toute base de l'espace E de dimension finie est associé un drapeau constitué des espaces successivement engendrés : .

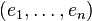
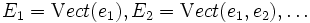
Réciproquement, un drapeau possède plusieurs bases adaptées. On les obtient en choisissant des vecteurs e_i ainsi : e_i appartient à E_i mais pas à E_{i − 1}.

Drapeau stable par un endomorphisme

Si est un endomorphisme de , alors on dit que le drapeau est stable par si .

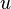
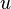
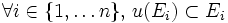
Par exemple si on reprend pour E l'espace et le drapeau formé des espaces successifs, un endomorphisme laisse stable ce drapeau à condition de diminuer (au sens large) le degré des polynômes. C'est le cas des endomorphismes de dérivation (P donne P'), de translation (P donne P(X+1)), etc.

Théorème de trigonalisation utilisant les drapeaux

Soit un endomorphisme de , espace vectoriel toujours supposé de dimension n. Alors les deux propositions suivantes sont équivalentes:

1. est trigonalisable.
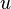
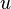
2. Il existe un drapeau de stable par . (ou un drapeau -stable)

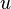
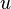
Les drapeaux dans le cadre euclidien

L'espace est de dimension finie et, en outre, muni d'un produit scalaire. Le procédé de Gram-Schmidt permet, à partir d'une base adaptée à un drapeau de E, d'obtenir une base orthonormale adaptée à ce même drapeau.

Si on combine avec la propriété précédente, on constate que tout endomorphisme trigonalisable peut être trigonalisé en base orthonormale.