Langage formel - Définition
Dans de nombreux contextes (scientifique, légal, etc.) l'on désigne par langage formel un mode d'expression plus formalisé et plus précis (les deux n'allant pas nécessairement de pair) que le langage de tous les jours (voir langage naturel).
En mathématiques, logique et informatique, un langage formel est formé :
- d'un ensemble de mots obéissant à des règles logiques strictes (dites grammaire formelle ou syntaxe).
- d'une sémantique sous-jacente.
La force des langages formels est de pouvoir faire abstraction de la sémantique, ce qui rend les théories réutilisables dans plusieurs modèles. Ainsi, alors qu'un calcul particulier de paye ou de matrice inverse restera toujours un calcul de paye ou de matrice inverse, un théorème sur les groupes s'appliquera aussi bien sur l'ensemble des entiers que sur les transformations du cube de Rubik.
Le langage formel, outil de travail
Le langage formel d'une discipline scientifique est un langage obéissant à une syntaxe formelle stricte, servant à exposer des énoncés de manière précise, si possible concise et sans ambiguïté ; ce qui l'oppose au langage naturel.
Langage formel contre langage naturel
Le langage formel a pour avantage de rendre aisées la manipulation et la transformation d'énoncés. Des règles de transformation précises (développement de formules logiques, formes normales, contrapositions, commutativité, associativité, etc.) peuvent être appliquées sans même connaître la signification de l'énoncé transformé ou la signification de la transformation. C'est un outil d'exploration puissant, et c'est le seul langage qui permette aux machines de " faire des mathématiques ".
L'inconvénient est évident : ne pas connaître le sens de l'énoncé empêche de savoir quelles sont les transformations pertinentes et nuit à l'intuition du raisonnement. Ainsi, il est bon de savoir lire rapidement un énoncé en langage formel et de le traduire tout aussi rapidement en un ou plusieurs énoncés du langage naturel, plus significatif.
Compréhension à l'aide d'ordinateurs
Dès le début de l'informatique les chercheurs ont développé des outils d'aide à la traduction des langages, afin de passer du format externe au format interne de l'ordinateur. Les outils les plus connus sont Lex et Yacc. D'autres chercheurs ont défini la sémantique des langages de programmation.
Dans l'histoire des mathématiques et des sciences
Avant le XXe siècle
Les mathématiques existent depuis l'antiquité mais la manière de les exprimer a énormément évolué.
Comme pour toute discipline, le langage de la discipline ne préexiste évidemment pas à la discipline elle-même. Il a donc fallu utiliser des langues qui n'ont pas été construites pour les mathématiques, qui peu à peu se sont enrichies d'un jargon spécifique.
Ainsi, bien des énoncés mathématiques anciens nous paraissent aujourd'hui avoir une formulation plutôt alambiquée, surchargée de périphrases quand il n'existe pas de mots pour désigner certains concepts.
Le jargon s'est donc enrichi au cours des siècles et continue encore d'évoluer.
Parallèlement à ce phénomène, s'est progressivement formé le langage formel qui est devenu celui que nous connaissons, le jargon naturel ne s'étant montré ni assez précis ni assez concis.
Au XXe siècle
Au début du XXe siècle, le mathématicien David Hilbert, et avec lui, les formalistes pensaient pouvoir unifier les mathématiques grâce à une axiomatisation générale et à l'usage d'un langage formel commun.
Cette vision des mathématiques fut mise à mal en 1931 lorsque le logicien Kurt Gödel annonça son célèbre théorème d'incomplétude qui stipule que dans tout système formel contenant l'arithmétique, il existe au moins une proposition indécidable.
Pour revenir aux langages formels, la conséquence de ce théorème est la suivante : étant donné un langage formel, ses axiomes, et son système de déduction formel capables d'exprimer l'arithmétique, on peut énoncer une proposition de ce langage qui ne peut pas être prouvée dans ce système, ainsi que sa négation. On aura beau formaliser les mathématiques, on trouvera toujours un énoncé formel dont la démonstration oblige à quitter ou élargir ce formalisme en ajoutant de nouveaux axiomes, ce qui introduira immanquablement de nouveaux énoncés indécidables. Ainsi l'approche formaliste, qui reste pourtant valable, a désormais des limites connues.
Dans la seconde moitié du XXe siècle, l'avènement des ordinateurs et de l'informatique a donné une place particulière aux langages formels en tant qu'outils et en tant qu'objets d'étude, ce qui était relativement nouveau.
Aujourd'hui (début du XXIe siècle)
Les traités de mathématiques utilisent à la fois langage formel et langage naturel. Le langage formel est réservé aux passages techniques et aux énoncés suffisamment simples pour ne pas nécessiter d'amples explications, et les résultats importants sont souvent explicités à la fois en langage formel et naturel.
Le langage formel mathématique contemporain est décrit dans cet article.
Les langages formels, objet d'étude
Les langages formels sont aussi l'objet d'étude d'une branche à part entière de la logique et de l'informatique théorique. Cette étude est fortement liée à la théorie de la calculabilité. En effet le propre d'un langage formel, en tant que langage, c'est de pouvoir être traité par un ordinateur, ou par son modèle formel : la machine de Turing.
Définitions
En tant qu'objet d'étude, un langage formel est défini comme un ensemble de mots de longueur finie (c'est-à-dire chaînes de caractères) déduit d'un certain alphabet fini, c'est-à-dire une partie du monoïde libre sur cet alphabet.
Typiquement, un alphabet serait : {a, b}, et un mot sur cet alphabet serait : ababba.
Un langage typique sur cet alphabet, et qui contiendrait ce mot, serait l'ensemble de tous les mots qui contiennent le même nombre de symboles a et b.
Le mot vide (le mot de longueur nulle) est autorisé et est noté ε. Bien que l'alphabet soit un ensemble fini et que chaque mot ait une longueur finie, un langage peut très bien contenir une infinité de mots (parce que la longueur de ses mots peut ne pas être bornée).
Exemples
Quelques exemples de langages formels :
- l'ensemble des mots sur {a, b},
- l'ensemble { an : n est un nombre premier },
- l'ensemble des programmes syntaxiquement corrects dans un langage de programmation donné,
- l'ensemble des mots d'entrée sur lesquels une machine de Turing donnée s'arrête.
Construction d'un langage formel
Un langage formel peut être spécifié par différents moyens, comme :
- les mots produits par des règles de production dites aussi règles d'une grammaire formelle (voir classification des langages),
- les mots générés par une expression rationnelle,
- les mots acceptés par un certain automate, comme une machine de Turing ou un automate d'états finis,
- l'ensemble des instances d'un problème de décision dont la réponse est OUI,
- des résultats d'inférences.
Plusieurs opérations peuvent être utilisées pour fabriquer de nouveaux langages à partir de ceux qu'on connaît. Supposons que L1 et L2 soient des langages sur un certain alphabet commun.
- La concaténation de L1 et L2 est l'ensemble des mots de la forme vw où v est un mot de L1 et w est un mot de L2. Notation :
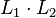
- L'intersection de L1 et L2 est l'ensemble des mots qui sont à la fois dans L1 et L2. Notation :
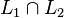
- L'union de L1 et L2 est l'ensemble des mots qui sont soit dans L1, soit dans L2. Notation :
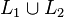
- Le complémentaire d'un langage L1 est l'ensemble des mots sur son alphabet qui ne sont pas contenus dans L1.
- Le quotient à droite de L1 et L2 est l'ensemble des mots v pour lesquels il existe un mot w de L2 tel que vw appartient à L1. Notation : L1 / L2.
- La fermeture de Kleene de L1 est l'ensemble des mots qui peuvent s'écrire
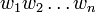
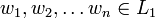
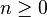
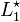
- Le renversé de L1 contient les mots de L1 écrits à l'envers. Notation :
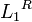
- Le mélangé de L1 et L2 est l'ensemble des mots pouvant s'écrire
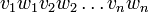
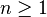
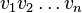
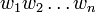
Appartenance, calculabilité et complexité
Des questions typiques que l'on se pose à propos d'un langage formel sont les suivantes:
- Peut-on décider par algorithme si un mot donné appartient à ce langage?
- Si oui, quelle est la complexité algorithmique d'une telle réponse?
Ces questions relèvent des domaines de la théorie de la calculabilité et de la théorie de la complexité.

















































