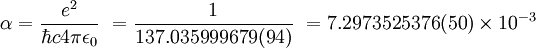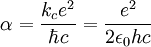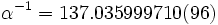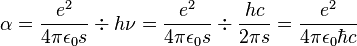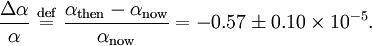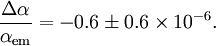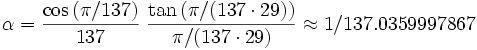Constante de structure fine - Définition

Articles de physique quantique |
| Théorie quantique |
| Électrodynamique quantique |
| Mécanique quantique |
| Théorie des champs |
| Modèle standard |
| Statistiques quantique |
| Bose-Einstein |
| Fermi-Dirac |
| Maxwell-Boltzmann |
| Physiciens |
| Bohr - de Broglie |
| Bose - Einstein |
| Fermi - Dirac |
| Heisenberg - Pauli |
| Schrödinger - Feynman |
La constante de structure fine, représentée par la lettre grecque α, est une constante fondamentale qui régit la force électromagnétique assurant la cohérence des atomes et des molécules. Elle fut proposée en 1916 par le physicien allemand Arnold Sommerfeld.
C’est un nombre sans dimension dont la valeur donnée par le CODATA en 2006 est :
Où

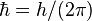

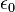
Autres définitions
La constante de structure fine peut aussi être définie par :
où
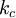

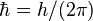

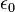
Dans le système d'unités CGS, l'unité de charge électrique (le Statcoulomb ou l'esu) est définie de telle façon que le facteur de permittivité,
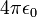
-
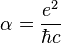
Mesure
La définition de


L'électrodynamique quantique (QED) propose une relation entre le moment magnétique de l'électron (autrement dit, le facteur de Landé
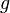

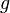

autrement dit une valeur avec une précision de 0.70 ppb. L'incertitude est dix fois plus petite que la meilleure des méthodes concurrentes utilisant les mesures de recul atomique. Les comparaisons entre les valeurs mesurée et calculée de
Interprétation physique
La constante de structure fine peut être vue comme le carré du rapport entre la charge élémentaire et la charge de Planck.
-
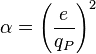
Pour toute longueur



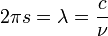
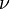
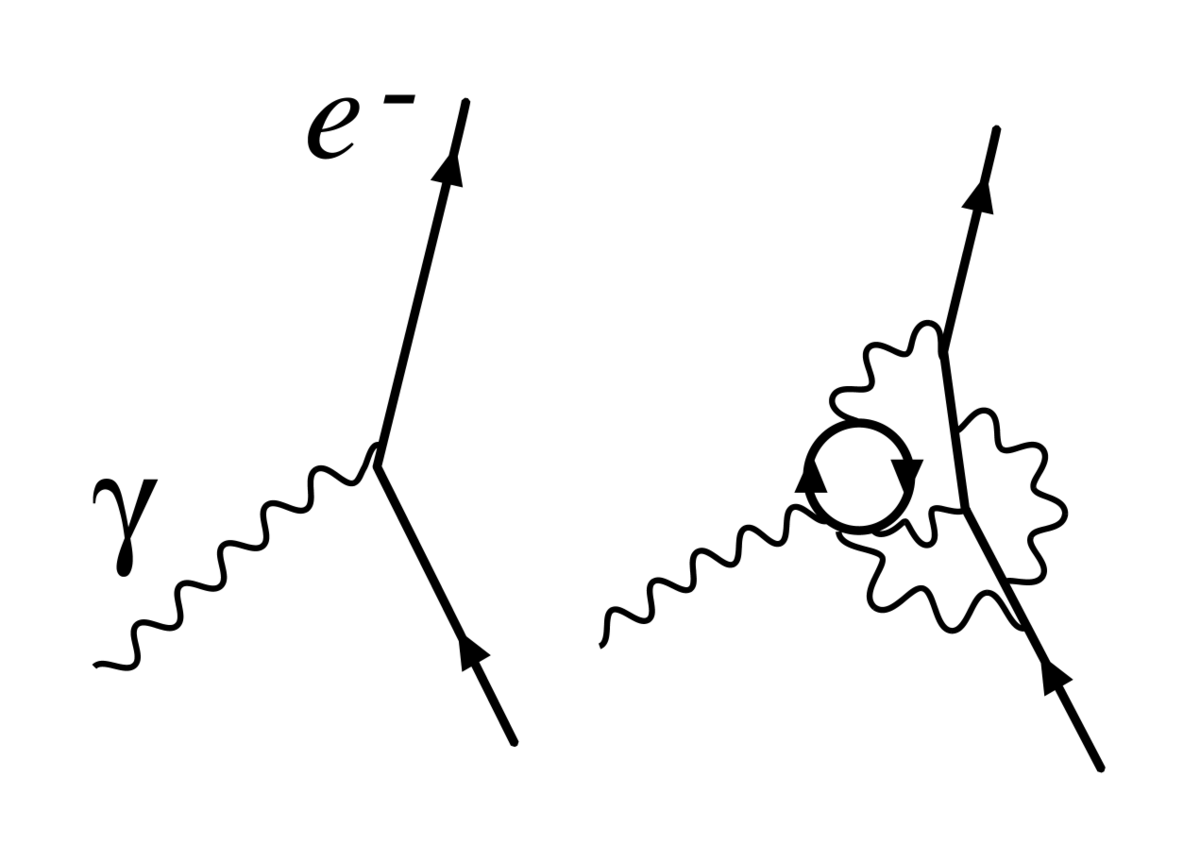
Dans la théorie électrodynamique quantique, la constante de structure fine joue le rôle de constante de couplage, représentant la force d'interaction entre les électrons et les photons. Sa valeur ne peut être prédite par la théorie mais seulement déterminée par des résultats expérimentaux. Il s'agit en fait de l'un des 29 paramètres libres du modèle standard de la physique des particules.
Le fait que



Dans la théorie électrofaible, théorie qui unifie l'interaction faible avec l'électromagnétisme, la constante de structure fine est intégrée dans deux autres constantes de couplage associées aux champs de jauge électrofaibles. Dans cette théorie, l'interaction électromagnétique est traitée comme un mélange d'interactions associées aux champs électrofaibles.
D'après la théorie de groupe de renormalisation, la valeur de


Historique
La constante de structure fine a été introduite pour la première fois en physique en 1916 par Arnold Sommerfeld. Elle mesurait les écarts relativistes entre les raies spectrales atomiques d'après les prédictions du modèle de Bohr.
Historiquement, la première interprétation physique de la constante de structure fine était qu'il s'agissait du rapport entre la célérité de l'électron sur la première orbite circulaire de l'atome de Bohr relativiste et la vitesse de la lumière dans le vide. De façon équivalente, c'était le quotient entre le moment angulaire maximum autorisé par la Relativité pour une orbite fermée et le moment angulaire minimum permis par la mécanique quantique. Elle apparaît dans l'analyse de Sommerfeld et détermine la taille de la séparation de la structure fine des raies spectrales de l'hydrogène.
Est-elle réellement constante ?
Les physiciens se demandent si cette constante en est vraiment une, c’est-à-dire si sa valeur ne varie pas avec le temps et suivant la position. Historiquement, il fut proposé un


Plus récemment, les avancées technologiques ont rendu possible l'évaluation de


En utilisant les Télescopes Keck et une série de données sur 128 quasars avec un décalage vers le rouge de 0,5
Une étude plus récente de 23 systèmes absorbants menée par Chand et al. utilise le Very Large Telescope et montre qu'il n'y a aucune variation mesurable :[13],[14]
Le résultat de Chand et al. écarte apparemment la variation avancée par Webb et al., bien qu'il subsiste des incertitudes concernant des erreurs systématiques. Des études complémentaires sont en cours pour obtenir d'avantage de données. Pour l'instant, tous les autres résultats obtenus confirment la constance de

Et si cette constante en est vraiment une, alors se pose la question de sa nature mathématique : rationnelle, algébrique ou transcendante ?
Explication anthropique
Une explication controversée de la valeur de la constante de structure fine fait appel au principe anthropique. Elle affirme que la valeur de



Explications numériques
La constante de structure fine a longtemps été un objet de fascination pour les physiciens car elle ne semble pas directement liée à des constantes mathématiques. Richard Feynman, l'un des fondateurs de l'électrodynamique, la comparait au " plus grand mystère de la physique : un nombre magique qui va au-delà de la compréhension de l'homme. "[16] Vers la fin de sa vie, le physicien Arthur Eddington établit des " preuves " numériques que
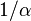
Sur les traces d'Eddington, le mathématicien James Gilson (lien) suggéra que la constante de structure fine était mathématiquement donnée par :
avec un grand degré de précision. 29 et 137 sont respectivement le 10ème et le 33ème nombre premier. La formule provient de la valeur de α donnée par le CODATA 2006, à une incertitude de mesure près.
Notes et références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais : " "
- ↑ (en) G. Gabrielse, D. Hanneke, T. Kinoshita, M. Nio, et B. Odom, New Determination of the Fine Structure Constant from the Electron g Value and QED, vol. 97, Physical Review Letters, 2006 [lire en ligne], p. 030802
- ↑ (en) Edward Arthur Milne, Relativity, Gravitation and World Structure, The Clarendon press, 1935
- ↑ (en) P. A. M. Dirac,, Nature, 1937, vol. 139, p. 323 .
- ↑ (en) G. Gamow,, Physical Review Letters, 1967, vol. 19, p. 757 et 913 .
- ↑ (en) John-Philippe Uzan,The fundamental constants and their variation: observational status and theoretical motivations, Reviews of Modern Physics, 2003, vol. 75, p. 403-455 [texte intégral].
- ↑ (en) John-Philippe Uzan, Variation of the constants in the late and early universe, vol. astro-ph 0409424, arXiv, 2004 [lire en ligne]
- ↑ (en) Keith Olive et Yong-Zhong Qian,Were Fundamental Constants Different in the Past ?, Physics Today, 2003, vol. 57 (10), p. 40-5 .
- ↑ (en) John D. Barrow, The Constants of Nature: From Alpha to Omega--the Numbers That Encode the Deepest Secrets of the Universe, Random House, coll. " Vintage ", Londres, 2002 (ISBN 0-09-928647-5)
- ↑ (en) John K. Webb et al.,Search for Time Variation of the Fine Structure Constant, Physical Review Letters, 1999, vol. 82 (5), p. 884-887 [texte intégral].
- ↑ (en) M. T. Murphy et al.,, Mon. Not. Roy. Astron. Soc., 2001, vol. 327, p. 1208 .
- ↑ (en) John K. Webb et al.,Further Evidence for Cosmological Evolution of the Fine Structure Constant, Physical Review Letters, 2001, vol. 87 (9), p. 091301 [texte intégral].
- ↑ (en) M.T. Murphy, J.K. Webb et V.V. Flambaum,{{{2}}}, Mon. Not R. astron. Soc., 2003, vol. 345, p. 609 .
- ↑ (en) H. Chand et al.,, Astron. Astrophys., 2004, vol. 417, p. 853 .)
- ↑ (en) R. Srianand et al.,, Physical Review Letters, 2004, vol. 92, p. 121302 .
- ↑ (en) John D. Barrow,Varying Constants, Philosophical Transactions of the Royal Society, 2005, vol. 363, p. 2139-2153 [texte intégral].
- ↑ (en) Richard Feynman, QED: The Strange Theory of Light and Matter, Princeton University Press, 1985 (ISBN 0-691-08388-6), p. 129