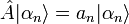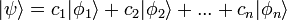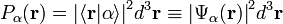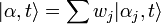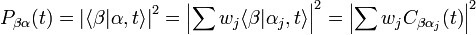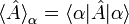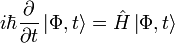Postulats de la mécanique quantique - Définition

Articles de physique quantique |
| Théorie quantique |
| Électrodynamique quantique |
| Mécanique quantique |
| Théorie des champs |
| Modèle standard |
| Statistiques quantique |
| Bose-Einstein |
| Fermi-Dirac |
| Maxwell-Boltzmann |
| Physiciens |
| Bohr - de Broglie |
| Bose - Einstein |
| Fermi - Dirac |
| Heisenberg - Pauli |
| Schrödinger - Feynman |
La description du monde microscopique que fournit la mécanique quantique s'appuie sur une vision radicalement nouvelle, et s'oppose en cela à la mécanique classique. Elle repose sur des postulats, ou axiomes.
Introduction
Les implications de cette nouvelle vision sont si complexes, profondes et inhabituelles (par rapport à notre propre expérience) qu'une grande partie de la communauté scientifique a décidé de les éluder, et se contente d'utiliser la théorie, qui a fourni les prévisions les plus précises à ce jour.
Les tenants de cette approche, dite de l'école de Copenhague tiennent à peu près ce discours :
- Il importe de remarquer dès maintenant que ces postulats n'ont aucun sens (méta-)physique : ils ne décrivent pas l'univers. Ils sont purement formels, opératoires, en ce qu'ils décrivent les opérations adéquates, mais sans permettre de les interpréter, ni à fortiori d'expliquer pourquoi elles permettent de décrire les phénomènes et même de les prédire. C'est la raison pour laquelle on a pu dire :
- " si quelqu'un vous dit qu'il a compris la mécanique quantique, c'est un menteur "
- Il s'agit d'une impossibilité radicale, liée à l'absence de lien physique entre les postulats et la réalité, et non d'une " simple " ignorance qui pourrait être comblée à l'intérieur du cadre de la mécanique quantique actuelle.
- Bref, la mécanique quantique est parfaitement valide dès maintenant (en attendant une surprise toujours possible…), mais incompréhensible sans complément encore à faire.
Parallèlement, une partie de la communauté scientifique ne pouvant accepter l'approche de l'école de Copenhague a tenté de créer une " autre " mécanique quantique qui serait en accord avec les principes " naturels " sur lesquels toute science expérimentale devrait s'appuyer : la reproductibilité d'une expérience et le principe de déterminisme.
Dans ce but, de nombreuses théories aussi sérieuses que farfelues ont vu le jour. La première solution proposée fut celle des variables cachées (théorie qui suppose que l'information " manquante " pour que le système se comporte d'une manière déterministe absolue est portée par des variables dont nous n'avons pas la connaissance). Malheureusement, nous savons à l'heure actuelle qu'il est impossible de résoudre tous les systématiques à l'aide d'une théorie de cette forme.
Une autre solution à cette problématique est le fait d'accepter la mécanique quantique et ces " problème de déterminisme ", mais, en opposition à l'école de Copenhague, de ne pas accepter le caractère fondamental des postulats de la mécanique quantique. Pour ce faire, les membres de cette école, ont porté leur analyse sur les " axiomes " fondamentaux qui soutiennent les sciences expérimentales. Cette analyse a porté ces fruits, et cette école reformule ces axiomes de manière qu'une science ou mécanique basée sur cette " logique axiomatique " soit en accord avec la mécanique quantique[réf. nécessaire]. Cette solution est très peu connue dans le monde non scientifique et possède encore un grand nombre de détracteurs. Les discours des détracteurs et les réponses des protagonistes de cette solution peuvent se résumer ainsi :
- Les détracteurs
- Cette solution ne fait que déplacer le problème, car au lieu d'avoir une mécanique quantique basée sur cinq postulats " sortis de nulle part " vous avez trouvé une solution pour qu'elle soit basée sur trois axiomes " sortis de nulle part "[réf. nécessaire].
- Les protagonistes
- Premièrement il est nécessaire de comprendre à quel point toute science est basée sur une axiomatique fondamentale qui régit l'acquisition de données expérimentales et le traitement de ces données. En effet, l'idée de causalité, de déterminisme, de reproductivité d'une expérience sont des concepts fondamentaux sans lesquels il serait impossible à l'esprit humain de créer une science. Et ces concepts sont des axiomes ! Ces axiomes ont été formulés durant l'Antiquité et nous les avons acceptés jusqu'à présent sans aucun doute. Or avec l'arrivée de la physique moderne, et l'étude des particules élémentaires ces axiomes engendrent des paradoxes, il est donc clair que nous ne pouvons donc plus les accepter tel quel, il devient donc nécessaire de les reformuler. Nous n'avons pas déplacé le problème car nous avons réduit six postulats et un axiome en trois axiomes. Enfin, ces trois nouveaux axiomes sont bien plus " naturels " que les six postulats de la mécanique quantique[réf. nécessaire].
Formulation mathématique
La formulation mathématique de la mécanique quantique, dans son usage général, fait largement appel à la notation bra-ket de Dirac, qui permet de représenter de façon concise les opérations sur les espaces de Hilbert utilisés en analyse fonctionnelle. Cette formulation est souvent attribuée à John von Neumann.
Soit un espace séparable






Dans ce cadre, le principe d'incertitude d'Heisenberg devient un théorème au sujet des opérateurs non-commutatifs. En outre, on peut traiter des observables continues et discrètes ; dans le premier cas, l'espace de Hilbert est un espace de fonctions d'onde de carré intégrables.
Les postulats
Postulat I
Définition de l'état quantique
La connaissance de l'état d'un système quantique est complètement contenue, à l'instant t, dans un vecteur normalisable de l'espace des états


Postulat II
Mesure : définition d'une observable
À toute propriété observable, par exemple la position, l'énergie ou le spin, correspond un opérateur hermitien linéaire agissant sur les vecteurs d'un espace de Hilbert

Les opérateurs associés aux propriétés observables sont définis par des règles de construction qui reposent sur un principe de correspondance[1] :
- L'opérateur de position
-
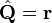
- L'opérateur d'énergie potentielle classique ou électromagnétique
-
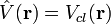
- L'opérateur de quantité de mouvement
-
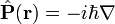

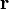
- L'opérateur de moment angulaire
-
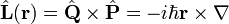
- L'opérateur d'énergie cinétique
-
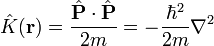
- L'opérateur d'énergie totale, appelé hamiltonien
-
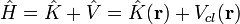
- L'opérateur action du système, appelé lagrangien
-
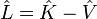
Postulat III
Mesure : valeurs possibles d'une observable
La mesure d'une grandeur physique représentée par l'observable A ne peut fournir que l'une des valeurs propres de A.
Les vecteurs propres et les valeurs propres de cet opérateur ont une signification spéciale : les valeurs propres sont les valeurs pouvant résulter d'une mesure idéale de cette propriété, les vecteurs propres étant l'état quantique du système lors de cette mesure. En utilisant la notation bra-ket, ce postulat peut s'écrire ainsi :
où

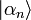
Les états propres de tout observable

Cela signifie que tout vecteur

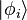
Postulat IV
Mesure : probabilité d'obtention d'une valeur d'une Observable
La mesure d'une grandeur physique représentée par l'observable A, effectuée sur l'état quantique (normalisé)

Le produit scalaire d'un état et d'un autre vecteur (qu'il appartienne ou non à

- Pour un système constitué d'une seule particule, la fonction d'onde est l'amplitude de probabilité que la particule est à la position
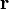
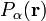
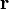
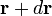
Donc
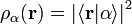
- Si le système est dans un état
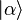
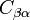
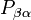
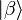
-
-
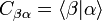
-
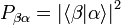
-
Ni
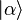
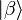
- Dans l'éventualité où un système peut évoluer vers un état
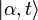
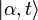
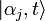
où
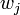
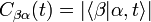
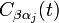
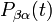
Mais si une mesure a déterminé que le trajet k a été suivi, alors les coefficients deviennent
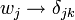
- En supposant que le système se trouve dans un état
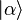

Postulat V
Mesure : réduction du paquet d'onde; obtention d'une valeur unique; projection de l'état quantique
Si la mesure de la grandeur physique A, à l'instant t, sur un système représenté par le vecteur

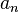
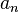
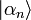
Ce postulat est aussi appelé "postulat de réduction du paquet d'onde".
Postulat VI
Evolution temporelle de l'état quantique
L'état
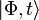
Le sixième postulat est l'équation de Schrödinger. Cette équation est l'équation dynamique de la mécanique quantique. Elle signifie simplement que c'est l'opérateur "énergie totale" du système ou hamiltonien, qui est responsable de l'évolution du système dans le temps. En effet, la forme de l'équation montre qu'en appliquant l'hamiltonien à la fonction d'onde du système, on obtient sa dérivée par rapport au temps c'est-à-dire comment elle varie dans le temps.
Cette équation n'est valable que dans le cadre non relativiste.