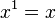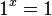1 (nombre) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| 1 | ||
|---|---|---|
| Cardinal | Un, Une | |
| Ordinal | premier, première prime (anc.) 1er, 1re | |
| Préfixe grec | mono | |
| Préfixe latin | uni | |
| Adverbe | premièrement | |
| Adverbe d'origine latine | primo | |
| Multiplicatif d'origine latine | semel | |
| Propriétés | ||
| Facteurs premiers | aucun | |
| Autres numérotations | ||
| Numération romaine | I | |
| Système binaire | 1 | |
| Système octal | 1 | |
| Système duodécimal | 1 | |
| Système hexadécimal | 1 | |
1 (un) est l'entier naturel représentant une entité seule. Un fait quelquefois référence à l'unité, et unitaire est quelquefois utilisé comme un adjectif dans ce sens. (Par exemple, un segment de longueur unitaire est un segment de longueur 1).
Évolution du glyphe
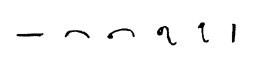
Le glyphe utilisé aujourd'hui dans le monde occidental pour représenter le nombre 1, une ligne verticale, souvent avec un petit empattement au sommet et quelques fois une petite ligne horizontale à la base, trouve ses racines chez les brahmanes Hindous. Ceux-ci écrivaient 1 sous forme d'une ligne horizontale (en Chine et au Japon aujourd'hui, c'est la manière dont il est écrit). Les Gupta l'écrivaient comme une ligne incurvée, et les Nagari quelquefois ajoutaient un petit cercle sur la gauche (tourné d'un quart de tour vers la droite, ceci ressemble au 9 puis devint l'écriture actuelle dans les écrits du Goujerat et du Panjâb). Les Népalais les tournaient aussi vers la droite, mais gardaient le petit cercle. Ceci devint finalement le serif du sommet dans l'écriture moderne, mais la petite ligne horizontale occasionnelle a probablement comme origine la ressemblance avec l'écriture romaine I.
En mathématiques
Pour tout nombre x :
-
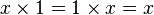
-
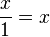
et pour
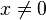
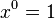
-
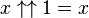
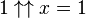
En utilisant l'addition ordinaire, nous avons 1 + 1 = 2 ; dépendant de l'interprétation du symbole « + » et du système de numération utilisé, l'expression peut avoir beaucoup de sens différents.
Un ne peut pas être utilisé comme base d'un système de numération positionnel de manière ordinaire. Quelquefois les marques de dénombrement sont assimilées à la « base 1 » ou système unaire, puisque seulement une marque (souvent un bâton) est nécessaire, mais cela ne marche pas de la même façon que le système de numération positionnelle. En liaison avec ceci il n'existe pas de logarithme en base 1, puisque la « fonction exponentielle » de base 1 est la fonction constante 1.
Dans la représentation de Von Neumann des nombres naturels, 1 est défini comme l'ensemble {0}. Il a un seul élément, c'est un ordinal et un cardinal, son rang héréditaire est 1.
On appelle singletons les ensembles ayant un seul élément.
Dans un groupe multiplicatif ou monoïde, l'élément neutre est quelquefois noté « 1 », mais « e » (issu de l'allemand Einheit, unité) est plus traditionnel. Néanmoins, « 1 » est spécialement dédié pour l'identité multiplicative d'un anneau. (Cette identité multiplicative est souvent appelée « unité ».)
Un est sa propre factorielle.
C'est aussi le premier et le deuxième nombre dans les suites de Fibonacci, et le premier nombre de beaucoup de suites mathématiques. Comme sujet de convention, le premier Livre de suites entières de Sloane ajoutait un 1 initial à chaque suite qui n'en avait pas déjà un, et considérait ces 1 initiaux dans leurs ordre lexicographique. Plus tard, Sloane dans son Encyclopédie des suites entières et sa contrepartie Web, l'Encyclopédie électronique des suites entières, ignora ces 1 initiaux dans leur ordre lexicographique des suites, car de tels 1 initiaux correspondent aux cas triviaux.
Un est le produit vide, lorsqu'il est l'élément neutre de la multiplication utilisée.
Un n'est pas actuellement considéré comme un nombre premier, bien qu'il soit parfois utilisé en tant que tel, à cause de l'erreur courante concernant la définition de la primalité : ce n'est pas "lorsque le nombre soit divisible seulement par un et lui-même" mais bien "lorsque le nombre ait deux diviseurs distincts, un et lui-même" (ce qui permet d'exclure le nombre un, qui n'a qu'un diviseur). D'ailleurs pour les usages de la factorisation et précisément pour le théorème fondamental de l'arithmétique, il est nécessaire et/ou suffisant de ne pas voir un comme un facteur premier, ou de le voir comme un facteur implicite qui existe toujours mais qui est non-écrit. Le dernier mathématicien professionnel à publier 1 en tant que nombre premier était Henri Lebesgue en 1899, bien que Carl Sagan incluait un dans une liste de nombres premiers dans son livre Contact en 1985.
Un est une des trois valeurs possibles retournées par la fonction de Möbius. En entrant un entier qui est sans carré avec un nombre pair de facteurs premiers distincts, la fonction de Möbius retourne un.
Un est le seul nombre impair qui soit dans l'image de la fonction indicatrice d'Euler (
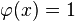
Par définition, 1 est la norme d'un vecteur unité et de la matrice unité.
Quelques propriétés arithmétiques de un
Un est son propre carré. En conséquence il est un nombre de Kaprekar. Un est le premier nombre figuré de chaque sorte, telle que les nombres triangulaires, nombres pentagonaux, nombres tétraédriques, nombres pyramidaux hexagonaux, nombres hexagonaux centrés...
Un est un nombre en division harmonique.
Un est le seul nombre parfait d'ordre 1 (voir nombre parfait multiple).
Un est égal à la somme de ses chiffres dans tout système de numération de base différente, c'est un nombre Harshad complet.
Un est un nombre méandrique, un nombre semi-méandrique et un nombre méandrique ouvert.