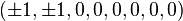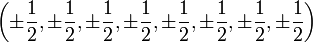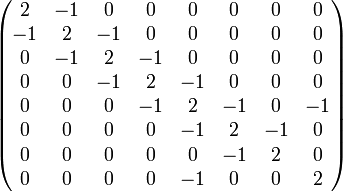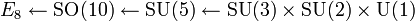E8 (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques,
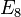
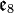
E est de rang 8 et de dimension 248. Il est simplement connexe et son centre est trivial.
La structure E a été découverte en 1887 par le mathématicien norvégien Sophus Lie pour étudier la symétrie et jusqu’ici personne ne pensait que cet objet mathématique pourrait être compris, considère Jeffrey Adams, responsable de l’équipe Atlas of Lie Groups and Représentations qui réunit 18 mathématiciens et programmeurs dans le monde, dont Fokko du Cloux et Marc van Leeuwen.
Formes réelles
En plus du groupe de Lie complexe E, de dimension complexe 248 (donc de dimension réelle 496), il existe trois formes réelles de ce groupe, toutes de dimension réelle 248. Les plus simples sont les formes compactes
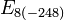
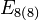
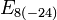
Géométrie
La forme réelle compacte de E peut être vue comme le groupe d'isométrie d'une variété riemannienne de dimension 128 appelée plan projectif octooctonionique. Ce nom vient de ce qu'il peut être construit en utilisant une algèbre qui est construite comme produit tensoriel des octonions avec eux-mêmes. Ce type de construction est analysé en détail par Hans Freudenthal et Jacques Tits dans leur construction du carré magique.
Constructions
On peut construire la forme compacte du groupe E comme le groupe d'automorphismes de l'algèbre de lie
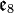
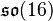
où
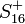
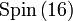
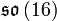
Si on appelle
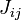
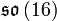
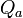
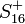
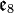
ainsi que
-
![\left[J_{ij}, Q_a\right] = \frac14 \left(\gamma_i\gamma_j - \gamma_j\gamma_i\right)_{ab}Q_b\,](https://static.techno-science.net/illustration/Definitions/autres/b/bf123d341c9502ae0e5452733a8004ea_aeb1702b7c9862d3bab586b741d0202a.png)
qui correspond à l'action naturelle de
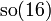
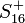
-
![\left[Q_a, Q_b\right] = \gamma^{[i}_{ac}\gamma^{j]}_{cb}J_{ij}\,](https://static.techno-science.net/illustration/Definitions/autres/5/51632689c8006bf6f240719672da191c_312c71660f2597172c12c254cce5f98e.png)
À partir de ces définitions on peut vérifier que l'identité de Jacobi est satisfaite.
Algèbre
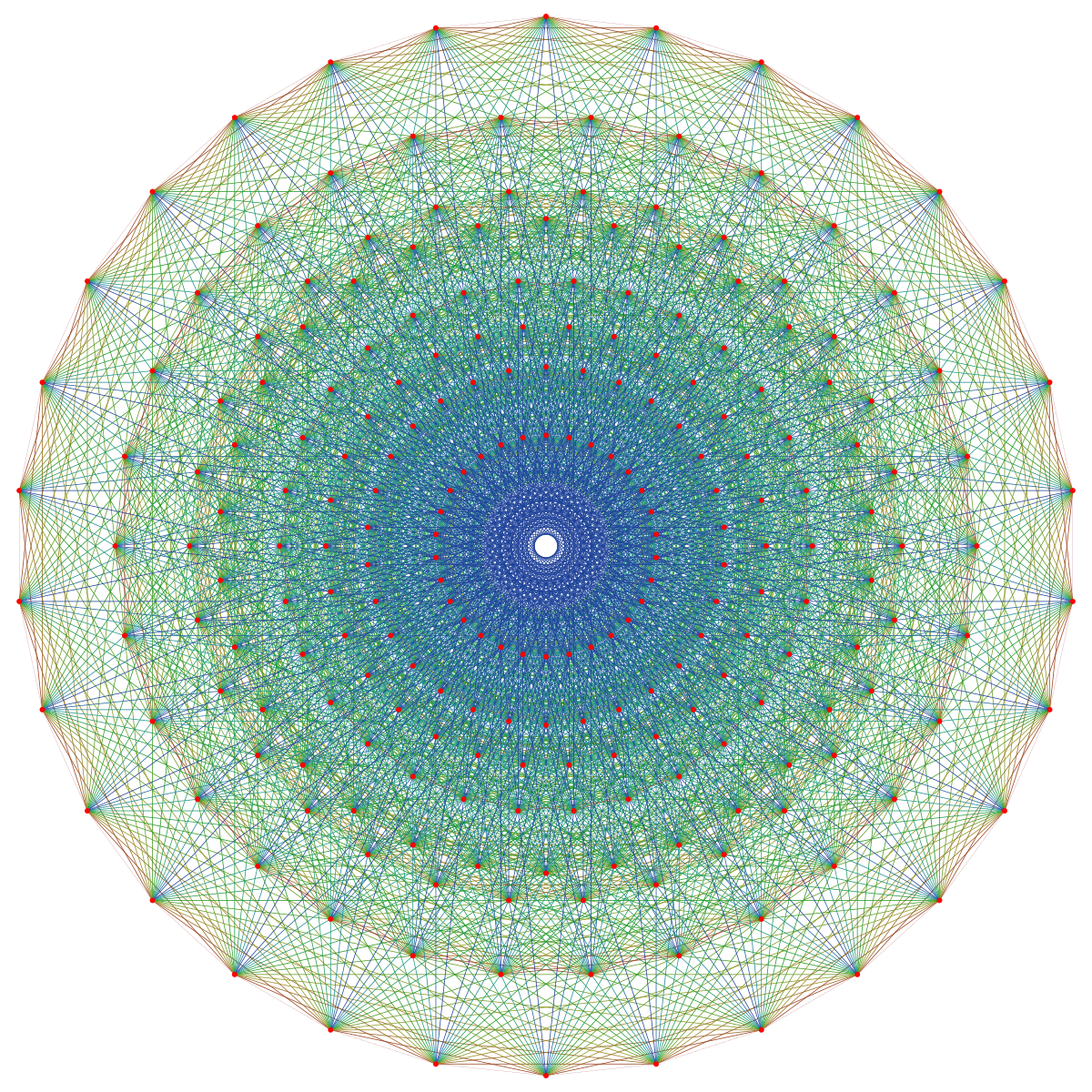
Diagramme de Dynkin
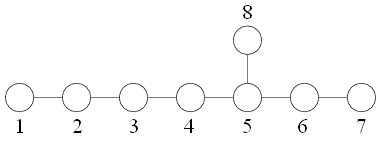
Système de racines
Dans la base formée par les racines simples
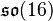
qui constitue le système de racines de
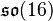
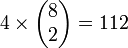
Par ailleurs on doit ajouter à cela les 128 poids de la représentation spinorielle
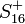
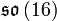
tels que la somme de toutes les coordonnées soit paire. Ils sont au nombre de
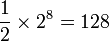
On obtient donc
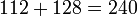
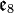
Matrice de Cartan
En physique
Dans le cadre des théories de grande unification en physique des particules, le groupe E est parfois considéré comme groupe de jauge candidat dans la mesure ou il contient d'une façon naturelle une série d'autres groupes de grande unifications souvent considérés. On peut le voir sous la succession d'inclusions
Par ailleurs, le groupe E apparait fréquemment en théorie des cordes et en supergravité. Dans la théorie des cordes hétérotiques une formulation fait apparaître
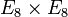
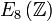
En novembre 2007, un physicien américain, Antony Garrett Lisi, dépose sur le site de publications scientifiques ArXiv un article très discuté sur une théorie unificatrice des forces basé sur le groupe E.
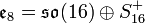
![\left[J_{ij}, J_{k\ell}\right] = \delta_{jk}J_{i\ell} - \delta_{j\ell}J_{ik} - \delta_{ik}J_{j\ell} + \delta_{i\ell}J_{jk}\,](https://static.techno-science.net/illustration/Definitions/autres/f/f8ddba45c26b81da3205c690d5648aeb_e7a2a40c9d311899698ac722d26a0f7f.png)